Chapter 3 HCF and LCM Set 3.5
Question 1.
Choose the right option.
i. The HCF of 120 and 150 is __
(A) 30
(B) 45
(C) 20
(D) 120
Solution:
(A) 30
Hint:
120 = 2 x 2 x 2 x 3 x 5
150 = 2 x 3 x 5 x 5
∴ HCF of 120 and 150 = 2 x 3 x 5 = 30
ii. The HCF of this pair of numbers is not 1.
(A) 13,17
(B) 29,20
(C) 40, 20
(D) 14, 15
Solution:
(C) 40, 20
Hint:
40 = 2 x 2 x 2 x 5
20 = 2 x 2 x 5
∴ HCF of 40 and 20 = 2 x 5 = 10
Question 2.
Find the HCF and LCM.
i. 14,28
ii. 32,16
iii. 17,102,170
iv. 23,69
v. 21,49,84
Solution:
i. 14 = 2 x 7
28 = 2 x 14
= 2 x 2 x 7
∴ HCF of 14 and 28 = 2 x 7
= 14
LCM of 14 and 28 = 2 x 2 x 7
= 28
ii. 32 = 2 x 16
= 2 x 2 x 8
= 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2
16 = 2 x 8
= 2 x 2 x 4
= 2 x 2 x 2 x 2
∴ HCF of 32 and 16 = 2 x 2 x 2 x 2
= 16
∴ LCM of 32 and 16 = 2 x 2 x 2 x 2 x 2
= 32
iii. 17 = 17 x 1
102 = 2 x 51
= 2 x 3 x 17
170 = 2 x 85
= 2 x 5 x 17
∴ HCF of 17, 102 and 170 = 17
∴ LCM of 17, 102 and 170 = 17 x 2 x 3 x 5
= 510
iv. 23 = 23 x 1
69 = 3 x 23
∴ HCF of 23 and 69 = 23
∴ LCM of 23 and 69 = 23 x 3
= 69
v. 21 = 3 x 7
49 = 7 x 7
84 = 2 x 42
= 2 x 2 x 21
= 2 x 2 x 3 x 7
∴ HCF of 21, 49 and 84 = 7
∴ LCM of 21, 49 and 84 = 7 x 3 x 7 x 2 x 2
= 588
Question 3.
Find the LCM.
i. 36, 42
ii. 15, 25, 30
iii. 18, 42, 48
iv. 4, 12, 20
v. 24, 40, 80, 120
Solution:
i. 36, 42

∴ LCM of 36 and 42 = 2 x 3 x 2 x 3 x 7
= 252
ii. 15, 25, 30
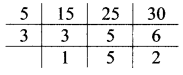
∴ LCM of 15, 25 and 30 = 5 x 3 x 5 x 2
= 150
iii. 18, 42, 48

∴ LCM of 18,42 and 48 = 2 x 3 x 2 x 2 x 3 x 7 x 2
= 1008
iv. 4, 12, 20
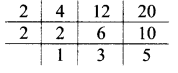
∴ LCM of 4, 12 and 20 = 2 x 2 x 3 x 5
= 60
v. 24, 40, 80, 120

∴ LCM of 24, 40, 80 and 120 = 2 x 2 x 2 x 5 x 3 x 2
= 240
Question 4.
Find the smallest number which when divided by 8,9,10,15,20 gives a remainder of 5 every time.
Solution:
Here, the smallest number for division is LCM of 8, 9, 10,15 and 20.
8 = 2 x 2 x 2
9 = 3 x 3
10 = 2 x 5
15 = 3 x 5
20 = 2 x 2 x 5
LCM of given numbers = 2 x 2 x 2 x 3 x 3 x 5 = 360
∴ Required, smallest number = LCM + Remainder
= 360 + 5
= 365
∴ The required smallest number is 365.
Question 5.
![]()
Solution:
i.
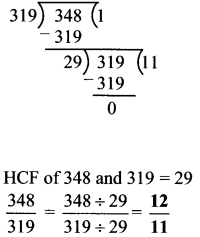
ii.
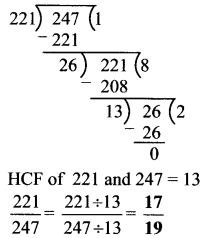
iii.
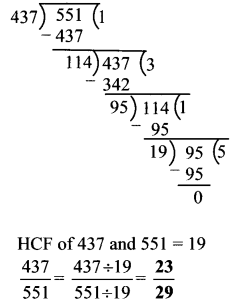
Question 6.
The LCM and HCF of two numbers are 432 and 72 respectively. If one of the numbers is 216, what is the other?
Solution:
Here, LCM = 432, HCF = 72, First number = 216
First number x Second number = LCM x HCF
∴ 216 x Second number = 432 x 72
![]()
∴ The other number is 144.
Question 7.
The product of two two-digit numbers is 765 and their HCF is 3. What is their LCM?
Solution:
Here, HCF = 3, Product of the given numbers = 765
Now, HCF x LCM = Product of the given numbers
∴ 3 x LCM = 765
![]()
∴ The LCM of the two two-digit numbers is 255.
Question 8.
A trader has three bundles of string 392 m, 308 m and 490 m long. What is the greatest length of string that the bundles can be cut up into without any left over string?
Solution:
The required greatest length of the string is the highest common factor (HCF) of 392, 308 and 490.
∴ 392 = 2 x 2 x 2 x 7 x 7
308 = 2 x 2 x 7 x 11
490 = 2 x 7 x 7 x 5
∴ HCF of 392, 308 and 490 = 2 x 7
= 14
∴ The required greatest length of the string is 14 m.

Question 9.
Which two consecutive even numbers have an LCM of 180?
Solution:
LCM of two consecutive even numbers = 180
But, HCF of two consecutive even numbers = 2
Now, product of the given number = HCF x LCM
= 2 x 180
= 360
To find the two consecutive even numbers, we have to factorize 360.
360 = 2 x 2 x 2 x 3 x 3 x 5
360 = (2 x 3 x 3) x (2 x 2 x 5)
= 18 x 20
∴ The two consecutive even numbers whose LCM is 180 are 18 and 20.