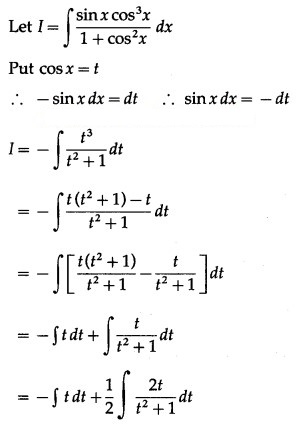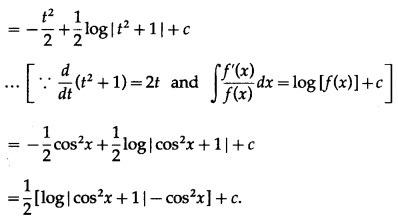Blog

Chapter 3 Indefinite Integration Ex 3.2(A)

Chapter 3 Indefinite Integration Ex 3.2(A)

I. Integrate the following functions w.r.t. x:

Question 1.

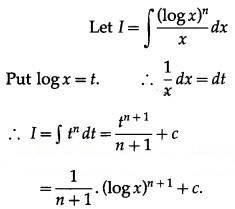
Question 2.

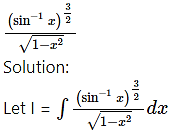
Question 3.

Solution:

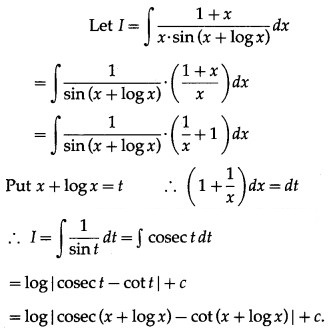
Question 4.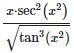

Solution:

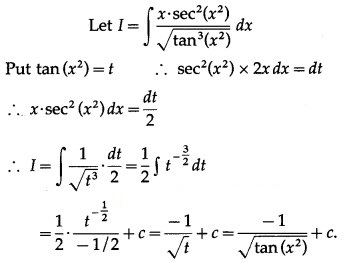
Question 5.

Solution:

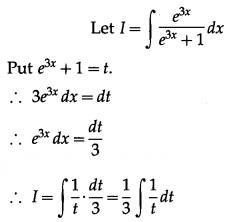
Question 6.

Solution:

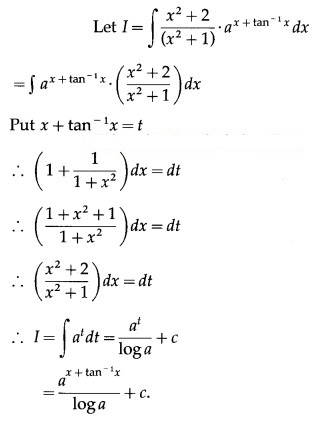
Question 7.

Solution:

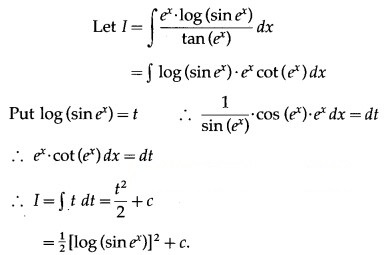
Question 8.

Solution:

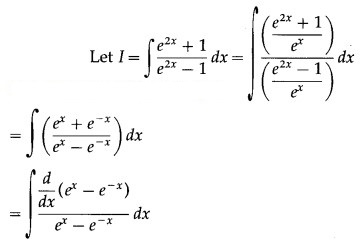
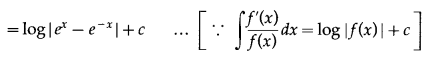
Question 9.

Solution:

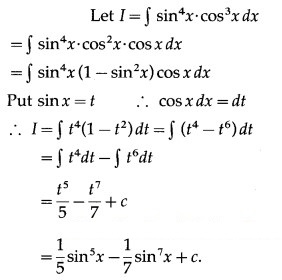
Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

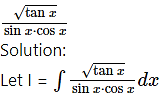
Dividing numerator and denominator by cos²x, we get

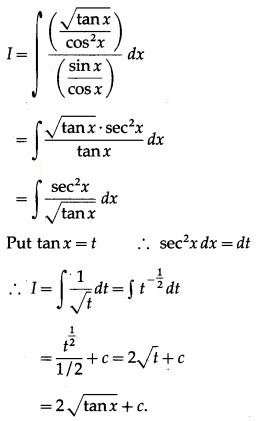
Question 14.

Solution:

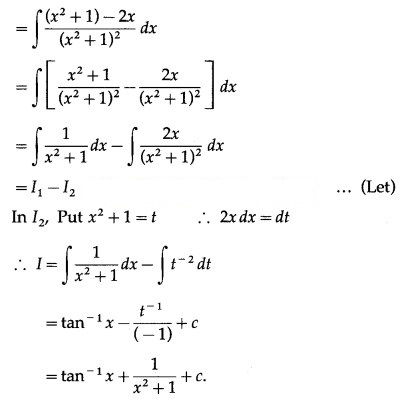
Question 15.

Solution:

Question 16.

Solution:

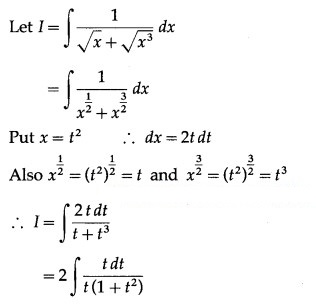
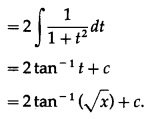
Question 17.

Solution:

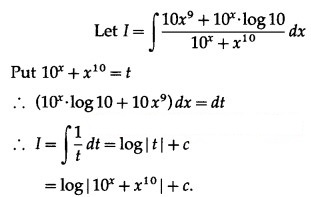
Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

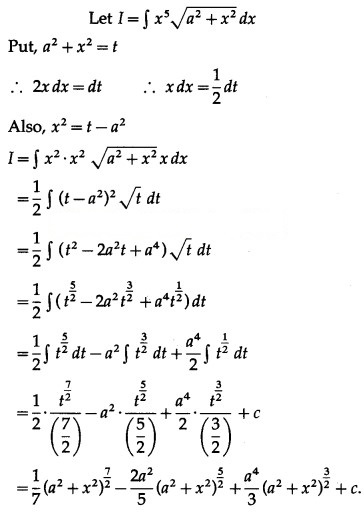
Question 21.

Solution:

Question 22.

Solution:

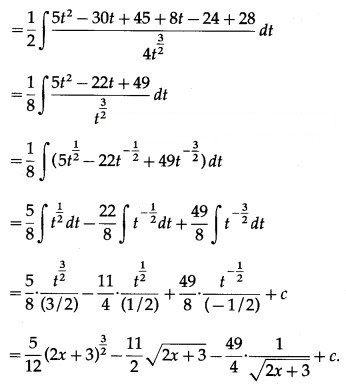
Question 23.

Solution:

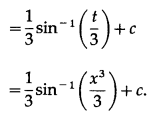
Question 24.

Solution:

Question 25.

Solution:

II. Integrate the following functions w.r.t x:

Question 1.

Solution:

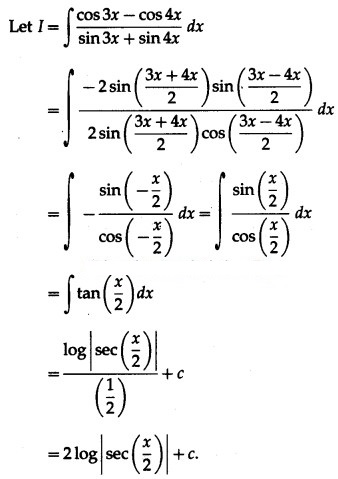
Question 2.

Solution:

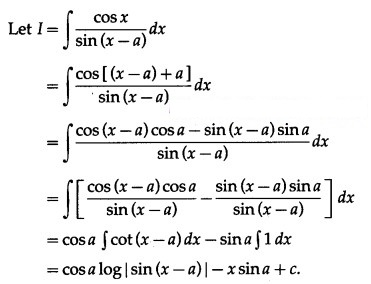
Question 3.

Solution:

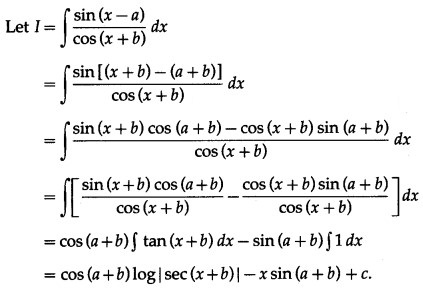
Question 4.

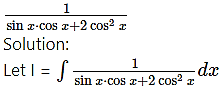
Dividing numerator and denominator of cos²x, we get

Question 5.

= A(3 sin x + 4 cos x) + B (3 cos x – 4 sin x)
∴ sin x + 2 cos x = (3A – 4B) sin x + (4A + 3B) cos x
Equating the coefficients of sin x and cos x on both the sides, we get
3A – 4B = 1 …… (1)
and 4A + 3B = 2 …… (2)
Multiplying equation (1) by 3 and equation (2) by 4, we get
9A – 12B = 3
16A + 12B = 8
On adding, we get

Question 6.



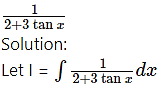
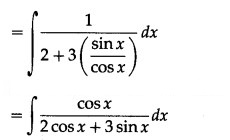
= A (2 cos x + 3 sin x) + B (-2 sin x + 3 cos x)
∴ cos x = (2A + 3B) cos x + (3A – 2B) sin x
Equating the coefficients of cos x and sin x on both the sides, we get
2A + 3B = 1 …… (1)
and 3A – 2B = 0 ……. (2)
Multiplying equation (1) by 2 and equation (2) by 3, we get
4A + 6B = 2
9A – 6B = 0
On adding, we get

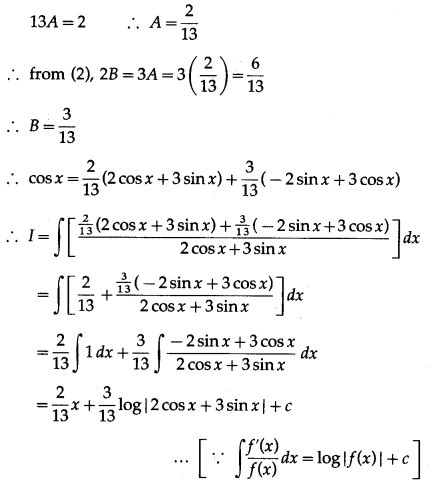
Question 7.

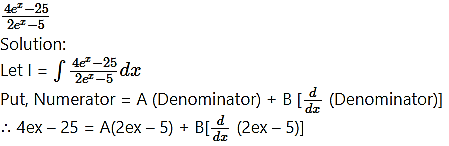
= A(2ex – 5) + B(2ex – 0)
∴ 4ex – 25 = (2A + 2B) ex – 5A
Equating the coefficient of ex and constant on both sides, we get
2A + 2B = 4 …….(1)
and 5A = 25
∴ A = 5
from (1), 2(5) + 2B = 4
∴ 2B = -6
∴ B = -3

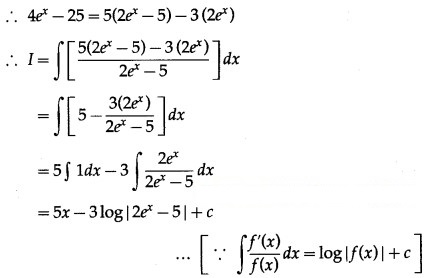
Question 8.

Solution:

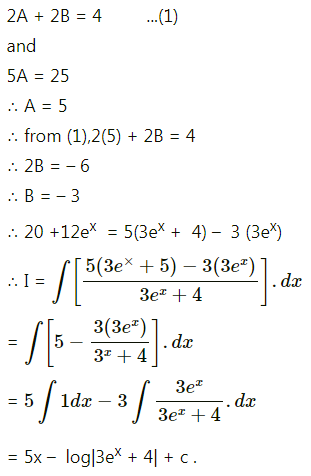
Question 9.

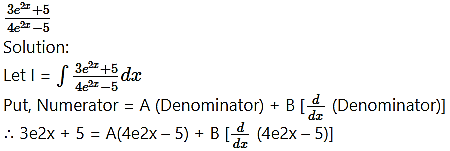
= A(4e2x – 5) + B(4 . e2x × 2 – 0)
∴ 3e2x + 5 = (4A + 8B) e2x – 5A
Equating the coefficient of e2x and constant on both sides, we get
4A + 8B = 3 …….. (1)
and -5A = 5
∴ A = -1
∴ from (1), 4(-1) + 8B = 3
∴ 8B = 7
∴ B = 7/8

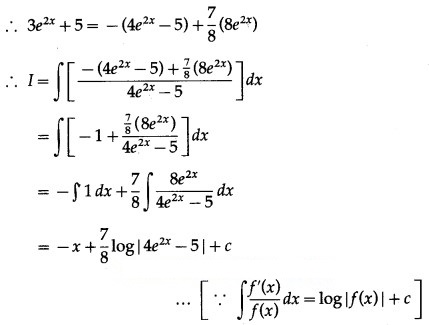
Question 10.
x . cot x
Solution:

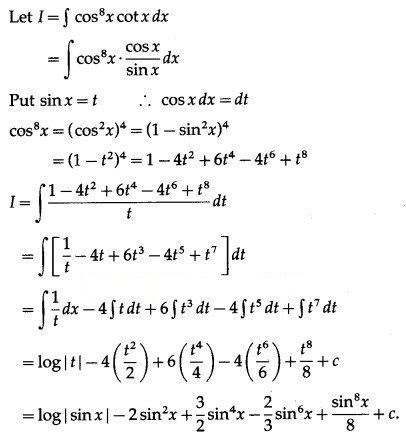
Question 11.

Solution:
Let I = ∫ dx

Question 12.

Solution:

Question 13.
tan 3x tan 2x tan x
Solution:
Let I = ∫ tan 3x tan 2x tan x dx

tan 3x (1 – tan 2x tan x) = tan 2x + tan x
tan 3x – tan 3x tan 2x tan x = tan 2x + tan x
tan 3x – tan 2x – tan x = tan 3x tan 2x tan x
I = ∫(tan 3x – tan 2x – tan x) dx
= ∫tan3x dx – ∫tan 2x dx – ∫tan x dx

Question 14.

Solution:

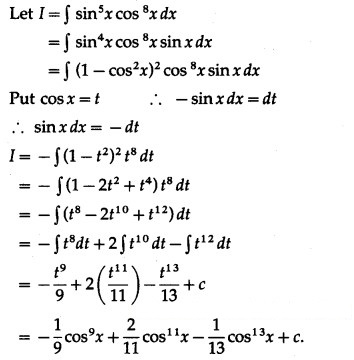
Question 15.

Solution:

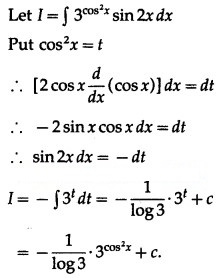
Question 16.

Solution:

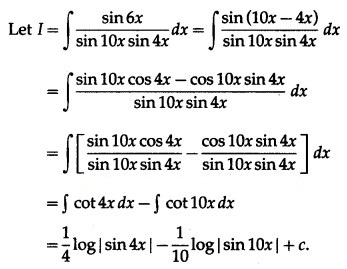
Question 17.

Solution: