Chapter 3 Indices and Cube Root Set 3.3
Question 1.
Find the cube root of the following numbers.
i. 8000
ii. 729
iii. 343
iv. -512
v. -2744
vi. 32768
Solution:
i. 8000
= 2 × 2 × 2 × 10 × 10 × 10
= (2 × 10) × (2 × 10) × (2 × 10)
= (2 × 10)³
= 20³
![]()

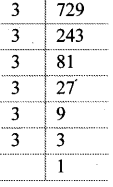
ii. 729
= (3 × 3) × (3 × 3) × (3 × 3)
= (3 × 3)³
= 9³
![]()
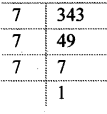
iii. 343
= 7 × 7 × 7
= 7³
![]()
iv. -512
= 2 × 2 × 2 × 4 × 4 × 4
= (2 × 4) × (2 × 4) × (2 × 4)
= (2 × 4)³
= 8³
∴ – 512 = (- 8) × (- 8) × (- 8)
= (-8)³
![]()

v. -2744
= 2 × 2 × 2 × 7 × 7 × 7
= (2 × 7) × (2 × 7) × (2 × 7)
= (2 × 7)³
= 14³
∴ -2744 = (-14) × (-14) × (-14)
= (-14)³
![]()

vi. 32768
= 2 × 2 × 2 × 4 × 4 × 4 × 4 × 4 × 4
= (2 × 4 × 4) × (2 × 4 × 4) × (2 × 4 × 4)
= (2 × 4 × 4)³
= 32³
![]()

Question 2.

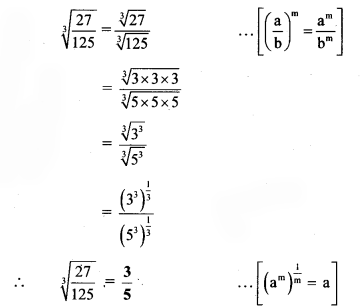
ii.
![]()

iii.
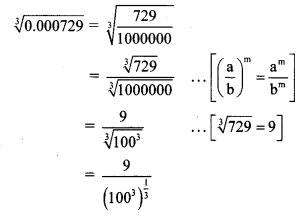
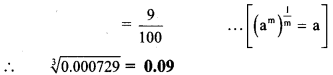
Note:
Here, number of decimal places in cube root = 6
∴ number of decimal places in cube of number = 2
Intext Questions and Activities
Question 1.
17 is a positive number. The cube of 17, which is 4913, is also a positive number. Cube of -6 is -216. Take some more positive and negative numbers and obtain their cubes. Find the relation between the sign of a number and the sign of its cube. (Textbook pg. no. 17)
Solution:
Consider, 6³ = 6 × 6 × 6 = 216 and (-4)³ = (- 4) × (- 4) × (- 4) = – 64
Thus, cube of a positive number is positive and cube of a negative number is negative.
∴ Sign of a number = sign of its cube.
Question 2.
In example 4 and 5 on textbook pg. no. 17, observe the number of decimal places in the number and number of decimal places in the cube of the number. Is there any relation between the two? (Textbook pg. no. 17)
Solution:
Yes, there is a relation between the number of decimal places in the number and its cube.
(1.2)³ = 1.728, (0.02)³ = 0.000008
No. of decimal places in 1.2 = 1
No. of decimal places in 1.728 = 3
No. of decimal places in 0.02 = 2
No. of decimal places in 0.000008 = 6
Thus, number of decimal places in cube of a number is three times the number of decimal places in that number.