Chapter 3 Permutations and Combination Ex 3.6
Chapter 3 Permutations and Combination Ex 3.6
Question 1.
Find the value of
(a) 15C4
Solution:
(b) 80C2
Solution:
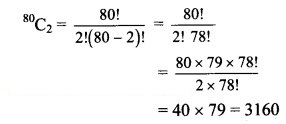
(c) 15C4 +15C5
Solution:
(d) 20C16 –19C16
Solution:

Question 2.
Find n if![]()
Solution:
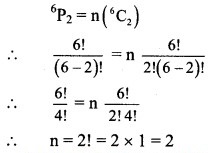
![]()
Solution:
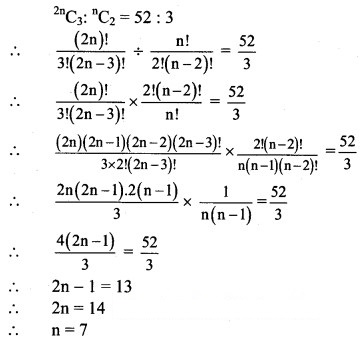
![]()
Solution:

Question 3.![]()
Solution:
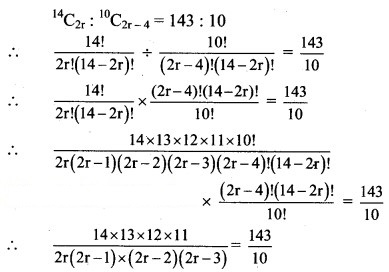
∴ 2r(2r – 1) (2r – 2) (2r – 3) = 14 × 12 × 10
∴ 2r(2r – 1) (2r – 2) (2r – 3) = 8 × 7 × 6 × 5
Comparing on both sides, we get
∴ r = 4
Question 4.
Find n and r if,![]()
Solution:

![]()
Solution:

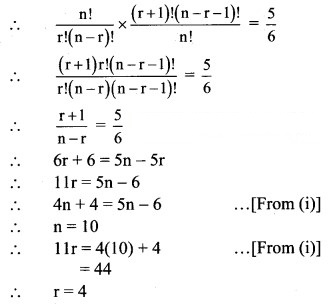
Question 5.![]()
Solution:
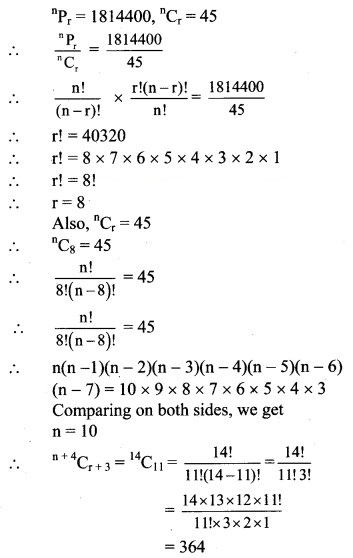
Question 6.![]()
Solution:

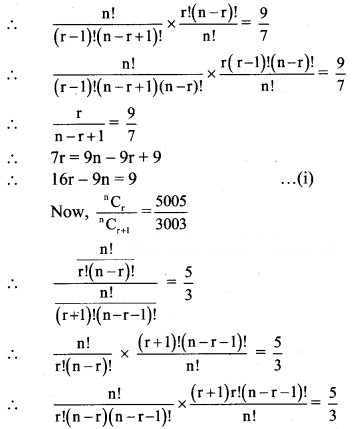
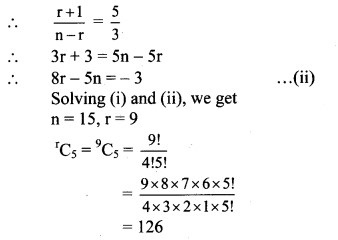
Question 7.
Find the number of ways of drawing 9 balls from a bag that has 6 red balls, 8 green balls, and 7 blue balls so that 3 balls of every colour are drawn.
Solution:
9 balls are to be selected from 6 red, 8 green, 7 blue balls such that the selection consists of 3 balls of each colour.

∴ Number of ways selection can be done if the selection consists of 3 balls of each colour
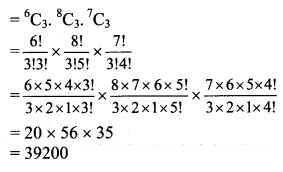
Question 8.
Find the number of ways of selecting a team of 3 boys and 2 girls from 6 boys and 4 girls.
Solution:
There are 6 boys and 4 girls.
A team of 3 boys and 2 girls is to be selected.
![]()
∴ Number of ways the team can be selected

Question 9.
After a meeting, every participant shakes hands with every other participants. If the number of handshakes is 66, find the number of participants in the meeting.
Solution:
Let there be n participants present in the meeting.
A handshake occurs between 2 persons.

132 = n (n – 1)
n(n – 1) = 12 × 11
Comparing on both sides, we get n = 12
∴ 12 participants were present at the meeting.
Question 10.
If 20 points are marked on a circle, how many chords can be drawn?
Solution:
To draw a chord we need to join two points on the circle.
There are 20 points on a circle.
∴ Total number of chords possible from these points

Question 11.
Find the number of diagonals of an n-sided polygon. In particular, find the number of diagonals when
(i) n = 10
(ii) n = 15
(iii) n = 12
(iv) n = 8
Solution:
In n-sided polygon, there are ‘n’ points and ‘n’ sides.
∴ Through ‘n’ points we can draw nC2 lines including sides.
∴ Number of diagonals in n sided polygon = nC2 – n (n = number of sides)
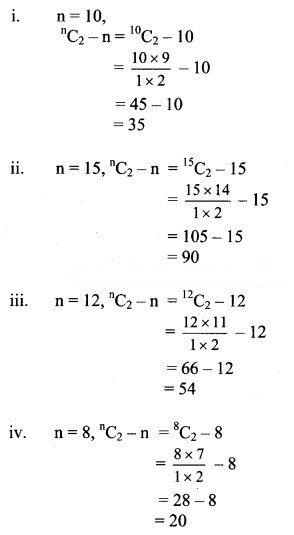
Question 12.
There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.
Solution:
There are 20 lines such that no two of them are parallel and no three of them are concurrent.
Since no two lines are parallel, they intersect at a point.
∴ Number of points of intersection if no two lines are parallel and no three lines are concurrent = 20C2
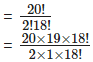
= 190
Question 13.
Ten points are plotted on a plane. Find the number of straight lines obtained by joining these points if (a) no three points are collinear (b) four points are collinear
Solution:
There are 10 points on a plane.
(a) When no three of them are collinear.
A line is obtained by joining 2 points.
∴ Number of lines passing through these points = 10C2

= 5 × 9
= 45
(b) When 4 of them are collinear.
If no three points are collinear, we get a total of 10C2 = 45 lines by joining them. …..[From (i)]
Since 4 points are collinear, only one line passes through these points instead of 4C2 lines.
∴ 4C2 – 1 extra lines are included in 45 lines.
Number of lines passing through these points
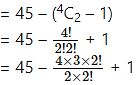
= 45 – 6 + 1
= 40
Question 14.
Find the number of triangles formed by joining 12 points if
(a) no three points are collinear
(b) four points are collinear
Solution:
There are 12 points on the plane.
(a) When no three of them are collinear.
A triangle can be drawn by joining any three non-collinear points.
∴ Number of triangles that can be obtained from these points = 12C3

= 220
(b) When 4 of these points are collinear.
If no three points are collinear, total we get 12C3 = 220 triangles by joining them. ……[From (i)]
Since 4 points are collinear, no triangle can be formed by joining these four points.

= 220 – 4
= 216
Question 15.
A word has 8 consonants and 3 vowels. How many distinct words can be formed if 4 consonants and 2 vowels are chosen?
Solution:
There are 8 consonants and 3 vowels.

= 3 ways.
Now, to form a word, these 6 ietters (i.e., 4 consonants and 2 vowels) can be arranged in 6P6 = 6! ways.
∴ Total number of words that can be formed = 70 × 3 × 6!
= 70 × 3 × 720
= 151200
∴ 151200 words of 4 consonants and 2 vowels can be formed.
Question 16.
Find n if,


Check:
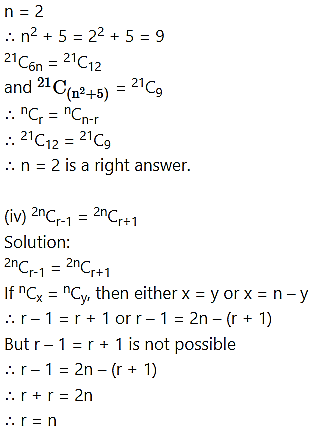
Check:

Question 17.![]()
Solution:

Question 18.![]()
Solution:

Question 19.![]()
Solution:

Question 20.
Find the differences between the greatest values in the following:
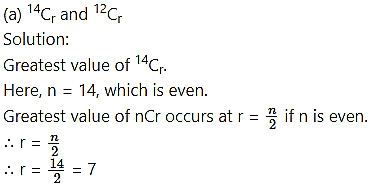

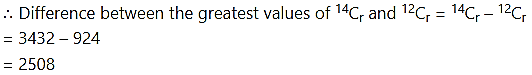
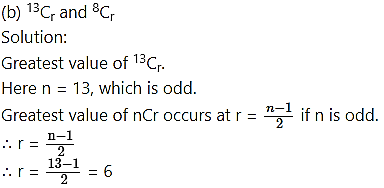

∴ Difference between the greatest values of 13Cr and 8Cr = 13Cr – 8Cr
= 1716 – 70
= 1646
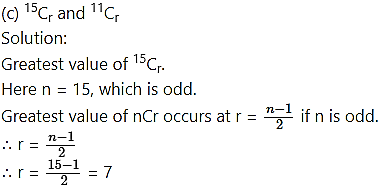
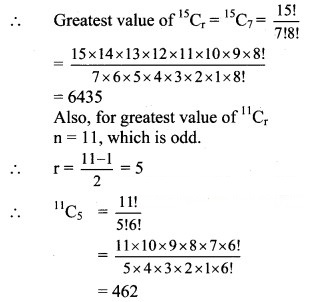
∴ Difference between the greatest values of 15Cr and 11Cr = 15Cr – 11Cr
= 6435 – 462
= 5973
Question 21.
In how many ways can a boy invite his 5 friends to a party so that at least three join the party?
Solution:
Boy can invite = (3 or 4 or 5 friends)
Consider the following table:

∴ Number of ways a boy can invite his friends to a party so that three or more of join the party = 10 + 5 + 1 = 16
Question 22.
A group consists of 9 men and 6 women. A team of 6 is to be selected. How many of possible selections will have at least 3 women?
Solution:
There are 9 men and 6 women.
A team of 6 persons is to be formed such that it consist of at least 3 women.
Consider the following table:

∴ No. of ways this can be done = 1680 + 540 + 54 + 1 = 2275
∴ 2275 teams can be formed if team consists of at least 3 women.
Question 23.
A committee of 10 persons is to be formed from a group of 10 women and 8 men. How many possible committees will have at least 5 women? How many possible committees will have men in majority?
Solution:
(i) A committee of 10 persons is to be formed from 10 women and 8 men such that the committee contains at least 5 women.
Consider the following table:

∴ Number of committees with at least 5 women
= 14112 + 14700 + 6720 + 1260 + 81
= 36873
(ii) Number of committees with men in majority = Total number of committees – (Number of committees with women in majority + women and men equal in number)
= 18C10 – 36873
= 18C10 – 36873
= 43758 – 36873
= 6885
Question 24.
A question paper has two sections. Section I has 5 questions and section II has 6 questions. A student must answer at least two questions from each section among 6 questions he answers. How many different choices does the student have in choosing questions?
Solution:
There are 11 questions, out of which 5 questions are from section I and 6 questions are from section II.
The student has to select 6 questions taking at least 2 questions from each section.
Consider the following table:

∴ Number of choices = 150 + 200 + 75 = 425
∴ In 425 ways students can select 6 questions, taking at least 2 questions from each section.
Question 25.
There are 3 wicketkeepers and 5 bowlers among 22 cricket players. A team of 11 player is to be selected so that there is exactly one wicketkeeper and at least 4 bowlers in the team. How many different teams can be formed?
Solution:
There are 22 cricket players, of which 3 are wicketkeepers and 5 are bowlers.
A team of 11 players is to be chosen such that exactly one wicket keeper and at least 4 bowlers are to be included in the team.
Consider the following table:

∴ Number of ways a team of 11 players can be selected
= 45045 + 6006
= 51051
Question 26.
Five students are selected from 11. How many ways can these students be selected if
(a) two specified students are selected?
(b) two specified students are not selected?
Solution:
5 students are to be selected from 11 students.
(a) When 2 specified students are included,
then remaining 3 students can be selected from (11 – 2) = 9 students.

= 84
∴ Selection of students is done in 84 ways when 2 specified students are included.
(b) When 2 specified students are not included, then 5 students can be selected from the remaining (11 – 2) = 9 students.

= 126
∴ Selection of students is done in 126 ways when 2 specified students are not included.