Chapter 3 Polynomials Practice Set 3.3

Chapter 3 Polynomials Practice Set 3.3

Question 1.
Divide each of the following polynomials by synthetic division method and also by linear division method. Write the quotient and the remainder.
i. (2m² – 3m + 10) ÷ (m – 5)
ii. (x⁴ + 2x³ + 3x² + 4x + 5) ÷ (x + 2)
iii. (y³ – 216) ÷ (y – 6)
iv. (2x⁴ + 3x³ + 4x – 2x²) ÷ (x + 3)
v. (x⁴ – 3x² – 8) ÷ (x + 4)
vi. (y³ – 3y² + 5y – 1) ÷ (y – 1)
Solution:
i. Synthetic division:
(2m² – 3m + 10) ÷ (m – 5)
Dividend = 2m² – 3m + 10
∴ Coefficient form of dividend = (2, -3, 10)
Divisor = m – 5
∴ Opposite of -5 is 5.
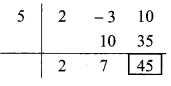
Maharashtra Board Class 9 Maths Solutions Chapter 3 Polynomials Practice Set 3.3 1

Coefficient form of quotient = (2, 7)
∴ Quotient = 2m + 7,
Remainder = 45
Linear division method:
2m² – 3m + 10
To get the term 2m², multiply (m – 5) by 2m and add 10m,
= 2m(m – 5) + 10m- 3m + 10
= 2m(m – 5) + 7m + 10
To get the term 7m, multiply (m – 5) by 7 and add 35
= 2m(m – 5) + 7(m- 5) + 35+ 10
= (m – 5) (2m + 7) + 45
∴ Quotient = 2m + 7,
Remainder = 45

ii. Synthetic division:
(x⁴ + 2x³ + 3x² + 4x + 5) ÷ (x + 2)
Dividend = x⁴ + 2x³ + 3x² + 4x + 5
∴ Coefficient form of dividend = (1, 2, 3, 4, 5)
Divisor = x + 2
∴ Opposite of + 2 is -2.
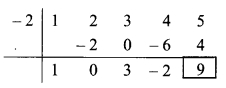
Maharashtra Board Class 9 Maths Solutions Chapter 3 Polynomials Practice Set 3.3 2
Coefficient form of quotient = (1, 0, 3, -2)
∴ Quotient = x³ + 3x – 2,
Remainder = 9

Linear division method:
x⁴ + 2x³ + 3x² + 4x + 5
To get the term x⁴, multiply (x + 2) by x³ and subtract 2x³,
= x³(x + 2) – 2x³ + 2x³ + 3x² + 4x + 5
= x³(x + 2) + 3x² + 4x + 5
To get the term 3x², multiply (x + 2) by 3x and subtract 6x,
= x³(x + 2) + 3x(x + 2) – 6x + 4x + 5
= x³(x + 2) + 3x(x + 2) – 2x + 5
To get the term -2x, multiply (x + 2) by -2 and add 4,
= x³(x + 2) + 3x(x + 2) – 2(x + 2) + 4 + 5
= (x + 2) (x3 + 3x – 2) + 9
∴ Quotient = x³ + 3x – 2,
Remainder – 9

iii. Synthetic division:
(y³ – 216) ÷ (y – 6)
Dividend = y³ – 216
∴ Index form = y³ + 0y³ + 0y – 216
∴ Coefficient form of dividend = (1, 0, 0, -216)
Divisor = y – 6
∴ Opposite of – 6 is 6.
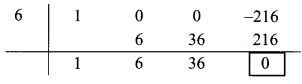
Maharashtra Board Class 9 Maths Solutions Chapter 3 Polynomials Practice Set 3.3 3
Coefficient form of quotient = (1, 6, 36)
∴ Quotient = y² + 6y + 36,
Remainder = 0

Linear division method:
y³ – 216
To get the term y³, multiply (y – 6) by y² and add 6y²,
= y²(y – 6) + 6y² – 216
= y²(y – 6) + 6ysup>2 – 216
To get the, term 6 y² multiply (y – 6) by 6y and add 36y,
= y²(y – 6) + 6y(y – 6) + 36y – 216
= y²(y – 6) + 6y(y – 6) + 36y – 216
To get the term 36y, multiply (y- 6) by 36 and add 216,
= y² (y – 6) + 6y(y – 6) + 36(y – 6) + 216 – 216
= (y – 6) (y² + 6y + 36) + 0
Quotient = y² + 6y + 36
Remainder = 0

iv. Synthetic division:
(2x⁴ + 3x³ + 4x – 2x²) ÷ (x + 3)
Dividend = 2x⁴ + 3x³ + 4x – 2x²
∴ Index form = 2x⁴ + 3x³ – 2x² + 4x + 0
∴ Coefficient form of the dividend = (2,3, -2,4,0)
Divisor = x + 3
∴ Opposite of + 3 is -3
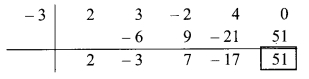
Maharashtra Board Class 9 Maths Solutions Chapter 3 Polynomials Practice Set 3.3 4
Coefficient form of quotient = (2, -3, 7, -17)
∴ Quotient = 2x³ – 3x² + 7x – 17,
Remainder = 51

Linear division method:
2x⁴ + 3x³ + 4x – 2x² = 2x² + 3x³ – 2x² + 4x
To get the term 2x⁴, multiply (x + 3) by 2x³ and subtract 6x³,
= 2x³(x + 31 – 6x³ + 3x³ – 2x² + 4x
= 2x³(x + 3) – 3x³ – 2x² + 4x

To get the term – 3x³, multiply (x + 3) by -3x² and add 9x²,
= 2x³(x + 3) – 3x²(x + 3) + 9x² – 2x² + 4x
= 2x³(x + 3) – 3x²(x + 3) + 7x² + 4x

To get the term 7x², multiply (x + 3) by 7x and subtract 21x,
= 2x³(x + 3) – 3x²(x + 3) + 7x(x + 3) – 21x + 4x
= 2x³(x + 3) – 3x²(x + 3) + 7x(x + 3) – 17x

To get the term -17x, multiply (x + 3) by -17 and add 51,
= 2x³(x + 3) – 3x²(x + 3) + 7x(x+3) – 17(x + 3) + 51
= (x + 3) (2x³ – 3x² + 7x- 17) + 51
∴ Quotient = 2x³ – 3x² + 7x – 17,
Remainder = 51

v. Synthetic division:
(x⁴ – 3x² – 8) + (x + 4)
Dividend = x⁴ – 3x² – 8
∴ Index form = x⁴ + 0x³ – 3x² + 0x – 8
∴ Coefficient form of the dividend = (1,0, -3,0, -8)
Divisor = x + 4
∴ Opposite of + 4 is -4
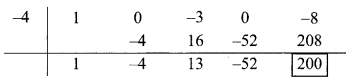
Maharashtra Board Class 9 Maths Solutions Chapter 3 Polynomials Practice Set 3.3 5
∴ Coefficient form of quotient = (1, -4, 13, -52)
∴ Quotient = x³ – 4x² + 13x – 52,
Remainder = 200

Linear division method:
x⁴ – 3x² – 8
To get the term x⁴, multiply (x + 4) by x³ and subtract 4x³,
= x³(x + 4) – 4x³ – 3x² – 8
= x³(x + 4) – 4x³ – 3x² – 8
To get the term – 4x³, multiply (x + 4) by -4x² and add 16x²,
= x³(x + 4) – 4x² (x + 4) + 16x² – 3x² – 8
= x³(x + 4) – 4x² (x + 4) + 13x² – 8
To get the term 13x², multiply (x + 4) by 13x and subtract 52x,
= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52x – 8
= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52x – 8
To get the term -52x, multiply (x + 4) by – 52 and add 208,
= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52(x + 4) + 208 – 8
= (x + 4) (x³ – 4x² + 13x – 52) + 200
∴ Quotient = x³ – 4x² + 13x – 52,
Remainder 200

vi. Synthetic division:
(y³ – 3y² + 5y – 1) ÷ (y – 1)
Dividend = y³ – 3y² + 5y – 1
Coefficient form of the dividend = (1, -3, 5, -1)
Divisor = y – 1
∴Opposite of -1 is 1.
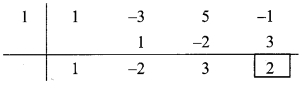
Maharashtra Board Class 9 Maths Solutions Chapter 3 Polynomials Practice Set 3.3 6
∴ Coefficient form of quotient = (1, -2, 3)
∴ Quotient = y² – 2y + 3,
Remainder = 2

Linear division method:
y³ -3y² + 5y – 1
To get the term y³ , multiply (y – 1) by y² and add y²
= y² (y – 1) + y² – 3y² + 5y – 1
= y² (y – 1) – 2y² + 5y – 1
To get the term -2y², multiply (y – 1) by -2y and subtract 2y,
= y² (y – 1) – 2y(y – 1) – 2y + 5y – 1
= y² (y – 1) – 2y(y – 1) + 3y – 1
To get the term 3y, multiply (y – 1) by 3 and add 3,
= y² (y – 1) – 2y(y – 1) + 3(y- 1) + 3 – 1
= (y – 1)(y² – 2y + 3) + 2
∴ Quotient = y² – 2y + 3,
Remainder = 2.