Chapter 3 Polynomials Practice Set 3.5
Chapter 3 Polynomials Practice Set 3.5
Question 1.
Find the value of the polynomial 2x – 2x3 + 7 using given values for x.
i. x = 3
ii. x = -1
iii. x = 0
Solution:
i. p(x) = 2x – 2x3 + 7
Put x = 3 in the given polynomial.
∴ p(3) = 2(3) – 2(3)3 + 7
= 6 – 2 x 27 + 7
= 6 – 54 + 7
∴ P(3) = – 41
ii. p(x) = 2x – 2x3 + 7
Put x = -1 in the given polynomial.
∴ p(- 1) = 2(- 1) – 2(-1)3 + 7
= – 2 – 2(-1) + 7
= -2 + 2 + 7
∴ p(-1) = 7
iii. p(x) = 2x – 2x3 + 7
Put x = 0 in the given polynomial.
∴ p(0) = 2(0) – 2(0)3 + 7
= 0 – 0 + 7
∴ P(0) = 7
Question 2.
For each of the following polynomial, find p(1), p(0) and p(- 2).
i. p(x) = x3
ii. p(y) = y2 – 2y + 5
ii. p(y) = x4 – 2x2 + x
Solution:
i. p(x) = x3
∴ p(1) = 13 = 1
p(x) = x3
∴ p(0) = 03 = 0
p(x) = x3
∴ p(-2) = (-2)3 = -8
ii. p(y) = y2 – 2y + 5
∴ p(1) = 12 – 2(1) + 5
= 1 – 2 + 5
∴ P(1) = 4
p(y) = y2 – 2y + 5
∴ p(0) = 02 – 2(0) + 5
= 0 – 0 + 5
∴ p(0) = 5
p(y) = y2 – 2y + 5
∴ p(- 2) = (- 2)2 – 2(- 2) + 5
= 4 + 4 + 5
∴ p(-2) = 13
iii. p(x) = x4 – 2x2 – x
∴ p(1) = (1)4 – 2(1)2 – 1
= 1 – 2 – 1
∴ p(1) = -2
∴ p(x) = x4 – 2x2 – x
∴ p(0) = (0)4 – 2(0)2 – 0
= 0 – 0 – 0
∴ p(0) = 0
p(x) = x4 – 2x2 – x
∴ p(-2) = (-2)4 – 2(-2)2 – (-2)
= 16 – 2(4) + 2
= 16 – 8 + 2
∴ p(-2) = 10
Question 3.
If the value of the polynomial m3 + 2m + a is 12 for m = 2, then find the value of a.
Solution:
p(m) = m3 + 2m + a
∴ p(2) = (2)3 + 2(2) + a
∴ 12 = 8 + 4 + a … [∵ p(2)= 12]
∴ 12 = 12 + a
∴ a = 12 – 12
∴ a = 0
Question 4.
For the polynomial mx2 – 2x + 3 if p(-1) = 7, then find m.
Solution:
p(x) = mx2 – 2x + 3
∴ p(- 1) = m (- 1)2 – 2(- 1) + 3
∴ 7 = m(1) + 2 + 3 …[∵ p(-1) = 7]
∴ 7 = m + 5
∴ m = 7 – 5
∴ m = 2
Question 5.
Divide the first polynomial by the second polynomial and find the remainder using remainder theorem.
i. (x2 – 1x + 9); (x + 1)
ii. (2x3 – 2x2 + ax – a); (x – a)
iii. (54m3 + 18m2 – 27m + 5); (m – 3)
Solution:
i. p(x) = x2 – 7x + 9
Divisor = x + 1
∴ take x = – 1
∴ By remainder theorem,
∴ Remainder =p(-1)
p(x) = x2 – 7x + 9
∴ p(-1) = (- 1)2 – 7(- 1) + 9
= 1 + 7 + 9
∴ Remainder =17
ii. p(x) = 2x3 – 2x2 + ax – a
Divisor = x – a
∴ take x = a
By remainder theorem,
Remainder = p(a)
p(x) = 2x3 – 2x2 + ax – a
∴ p(a) = 2a3 – 2a2 + a(a) – a
= 2a3– 2a2 + a2 – a
∴ Remainder = 2a3 – a2 – a
iii. p(m) = 54m3 + 18m2 – 27m + 5
Divisor = m – 3
∴ take m = 3
∴ By remainder theorem,
Remainder = p(3)
p(m) = 54m3 + 18m2 – 27m + 5
∴ p(3) = 54(3)3 +18(3)2 – 27(3) + 5
= 54(27) + 18(9) – 81 + 5
= 1458 + 162 – 81 + 5
∴ Remainder = 1544
Question 6.
If the polynomial y3 – 5y2 + 7y + m is divided by y + 2 and the remainder is 50, then find the value of m.
Solution:
p(y) = y3 – 5y2 + 7y + m
Divisor = y + 2
∴ take y = – 2
∴ By remainder theorem,
Remainder = p(- 2) = 50
P(y) = y3 – 5y2 + 7y + m
∴ P(-2) = (- 2)3 – 5(- 2)2 + 7(- 2) + m
∴ 50 = -8 – 5(4) – 14 + m
∴ 50 = -8 – 20 – 14 + m
∴ 50 = – 42 + m
∴ m = 50 + 42
∴ m = 92
Question 7.
Use factor theorem to determine whether x + 3 is a factor of x2 + 2x – 3 or not.
Solution:
p(x) = x2 + 2x – 3
Divisor = x + 3
∴ take x = – 3
∴ Remainder = p(-3)
p(x) = x2 + 2x – 3
∴ p(-3) = (-3)2 + 2(- 3) – 3
= 9 – 6 – 3
∴ p(-3) = 0
∴ By factor theorem, x + 3 is a factor of x2 + 2x – 3.
Question 8.
If (x – 2) is a factor of x3 – mx2 + 10x – 20, then find the value of m.
Solution:
p(x) = x3 – mx2 + 10x – 20 x – 2 is a factor of x3 – mx2 + lOx – 20.
∴By factor theorem,
Remainder = p(2) = 0
p(x) = x3 – mx2 + 10x – 20
∴ p(2) = (2)3 – m(2)2 + 10(2) – 20
∴ 0 = 8 – 4m + 20 – 20
∴ 0 = 8 – 4m
∴ 4m = 8
∴ m = 2
Question 9.
By using factor theorem in the following examples, determine whether q(x) is a factor of p(x) or not.
i. p(x) = x3 – x2 – x -1 ; q(x) = x – 1
ii. p(x) = 2x3 – x2 – 45 ; q(x) = x – 3
Solution:
i. p(x) = x3 – x2 – x – 1
Divisor = q(x) = x – 1
∴ take x = 1
Remainder = p(1)
p(x) = x3 – x2 – x – 1
∴ P(1) = (1)3 – (1)2 – 1 – 1
= 1 – 1 – 1 – 1
= -2 ≠ 0
∴ By factor theorem, x – 1 is not a factor of x3 – x2 – x – 1.
ii. p(x) = 2x3 – x – 45
Divisor = q(x) = x – 3
take x = 3
Remainder = p(3)
p(x) = 2x3 – x2 – 45
P(3) = 2(3)3 – (3)2 – 45
= 2(27) – 9 – 45
= 54 – 9 – 45
= 0
∴ By factor theorem, x – 3 is a factor of 2x3 – x2 – 45.
Question 10.
If (x31 + 31) is divided by (x + 1), then find the remainder.
Solution:
p(x) = x31 + 31
Divisor = x + 1
∴ take x = – 1
∴ By remainder theorem,
Remainder = p(-1)
p(x) =x31 + 31 …
∴ p(-1) = (-1)31 + 31
= -1 + 31 = 30
∴ Remainder = 30
Question 11.
Show that m – 1 is a factor of m21 – 1 and m22 – 1. [3 Marks]
Solution:
i. p(m) = m21 – 1
Divisor = m – 1
∴ take m = 1
Remainder = p(1)
p(m) = m21 – 1
∴ P(1) = 121 – 1 = 1 – 1 = 0
∴ By factor theorem, m -1 is a factor of m21 -1.
ii. p(m) = m22 – 1
Divisor = m – 1
∴ take m = 1
Remainder = p(1)
p(m) = m22 – 1
∴ P(1) = 122 – 1 = 1 – 1 = 0
∴ By factor theorem, m -1 is a factor of m22 – 1.
Question 12.
∴ 0 = n- 10 +4m … [Multiplying both sides by 4]
∴ n = 10 – 4m ……(ii)
Substituting n = 10 – 4m in equation (i),
4(10 – 4m) – 10 + m = 0
∴ 40 – 16m – 10 + m = 0
∴ -15m+ 30 = 0
∴ -15m = -30
∴ m = 2
Substituting m = 2 in equation (ii),
n = 10 – 4(2)
= 10 – 8
∴ n = 2
∴ m = n = 2
Question 13.
i. If p(x) = 2 + 5x, then find the value of p(2) + p(- 2) – p(1).
Solution:
p(x) = 2 + 5x
∴ P(2) = 2 + 5(2)
= 2 + 10
= 12
p(x) = 2 + 5x
P(- 2) = 2 + 5(- 2)
= 2 – 10 = – 8
p(x) = 2 + 5x
P(1) = 2 + 5(1)
= 2 + 5 = 7
∴ P(2) + P(- 2) – p(1) = 12 + (- 8) – 7
∴ P(2) + p(- 2) – p(1) = – 3
ii. If p(x) = 2x2 – 5√3 x + 5, then find the value of p(5√3 ).
Solution:
p(x) = 2x2 – 5√3 x + 5
∴ p(5√3) = 2(5√3)2 – 5√3 (5√3 ) + 5
= 2 (25 x 3) – 25 x 3 + 5
= 150-75 + 5
∴ p( 5√3 ) = 80
Question 1.
1. Divide p(x) = 3x2 + x + 7 by x + 2. Find the remainder.
2. Find the value of p(x) = 3x2 + x + 7 when x = – 2.
3. See whether remainder obtained by division is same as the value of p(-2). Take one more example and verify. (Textbook pg. no. 50)
Solution:
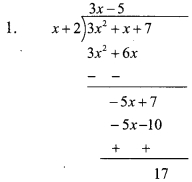
∴ Remainder = 17
2. p(x) = 3x2 + x + 7
Substituting x = – 2, we get
p(-2) = 3(2)2 + (-2) + 7
= 12 – 2 + 7
∴ p(-2) = 17
3. Yes, remainder = p(-2)
Another Example:
If the polynomial t3 – 3t2 + kt + 50 is divided by (t – 3), the remainder is 62. Find the value of k.
Solution:
When given polynomial is divided by (t – 3) the remainder is 62. It means the value of the polynomial when t = 3 is 62.
p(t) = t3 – 3t3 + kt + 50
By remainder theorem,
Remainder = p(3) = 33 – 32 + k x 3 + 50
= 27 – 3 x 9 + 3k + 50
= 27 – 27 + 3k + 50
= 3k + 50
But remainder is 62.
∴ 3k + 50 = 62
∴ 3k = 62 – 50
∴ 3k = 12
∴ k = 4
Question 2.
Verify that (x – 1) is a factor of the polynomial x3 + 4x – 5. (Textbook pg. no. 51)
Solution:
Here, p(x) = x3 + 4x – 5
Substituting x = 1 in p(x), we get
p(1) = (1)3 + 4(1) – 5
= 1 + 4 – 5
P(1) = 0
∴ By remainder theorem,
Remainder = 0
∴ (x -1) is the factor of x3 + 4x – 5.