Blog

Chapter 3 Trigonometric Functions Ex 3.1

Chapter 3 Trigonometric Functions Ex 3.1

Question 1.
Find the principal solutions of the following equations :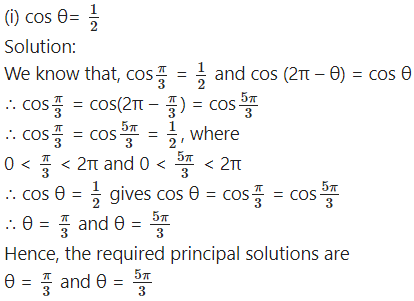

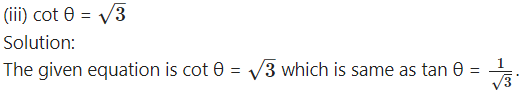
We know that,

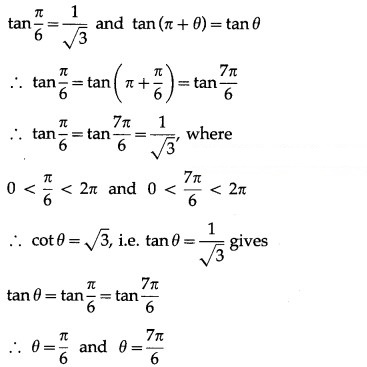
Hence, the required principal solution are

(iv) cot θ = 0.
Solution:

Question 2.
Find the principal solutions of the following equations:
(i) sinθ = −1/2
Solution:
We know that,
sin π/6 = 1/2 and sin (π + θ) = -sinθ,
sin(2π – θ) = -sinθ

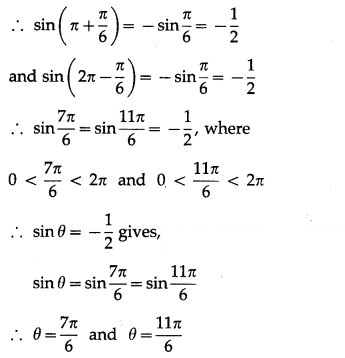
Hence, the required principal solutions are
θ = 7π/6 and θ = 11π/6.

(ii) tanθ = -1
Solution:
We know that,
tan π/4 = 1 and tan(π – θ) = -tanθ,
tan(2π – θ) = -tanθ

Hence, the required principal solutions are
θ = 3π/4 and θ = 7π/4.

(iii) √3 cosecθ + 2 = 0.
Solution:

Question 3.
Find the general solutions of the following equations :

Question 4.
Find the general solutions of the following equations:

(ii) cosecθ = –√2
Solution:
The general solution of sinθ = sin∝ is

(iii) tanθ = -1
Solution:
The general solution of tanθ = tan∝ is

Question 5.
Find the general solutions of the following equations :
(i) sin 2θ = 1/2
Solution:
The general solution of sin θ = sin ∝ is
θ = nπ + (-1)ⁿ∝, n ∈ Z

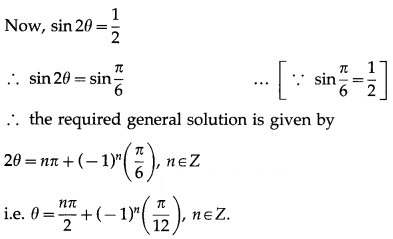
(ii) tan 2θ/3 = √3
Solution:
The general solution of tan θ = tan ∝ is

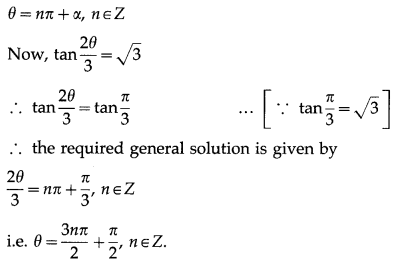
(iii) cot 4θ = -1
Solution:
The general solution of tan θ = tan ∝ is

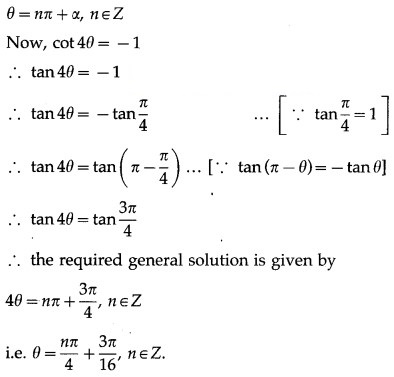
Question 6.
Find the general solutions of the following equations :
(i) 4 cos²θ = 3
Solution:
The general solution of cos²θ = cos² ∝ is
θ = nπ ± ∝, n ∈ Z
Now, 4 cos²θ = 3

(ii) 4 sin²θ = 1
Solution:
The general solution of sin²θ = sin² ∝ is
θ = nπ ± ∝, n ∈ Z
Now, 4 sin²θ = 3

(iii) cos 4θ = cos 2θ
Solution:
The general solution of cos θ = cos ∝ is
θ = 2nπ ± ∝, n ∈ Z
∴ the general solution of cos 4θ = cos 2θ is given by
4θ = 2nπ ± 2θ, n ∈ Z
Taking positive sign, we get
4θ = 2nπ + 2θ, n ∈ Z
∴ 2θ = 2nπ, n ∈ Z
∴ θ = nπ, n ∈ Z
Taking negative sign, we get
4θ = 2nπ – 2θ, n ∈ Z
∴ 6θ = 2nπ, n ∈ Z
∴ θ = nπ/3, n ∈ Z
Hence, the required general solution is
θ = nπ/3, n ∈ Z or ∴ θ = nπ, n ∈ Z.
Alternative Method:
cos 4θ = cos 2θ
∴ cos4θ – cos 20 = 0

∴ sin3θ∙sinθ = 0
∴ either sin3θ = 0 or sin θ = 0
The general solution of sin θ = 0 is
θ = nπ, n ∈ Z.
∴ the required general solution is given by
3θ = nπ, n ∈ Z or θ = nπ, n ∈ Z
i.e. θ = nπ3, n ∈ Z or θ = nπ, n ∈ Z.

Question 7.
Find the general solutions of the following equations :
(i) sinθ = tanθ
Solution:
sin θ = tan θ
∴ sin θ = sinθ/cosθ
∴ sin θ cos θ = sin θ
∴ sin θ cos θ – sinθ = 0
∴ sin θ (cos θ – 1) = θ
∴ either sinθ = 0 or cosθ – 1 = 0
∴ either sin θ = 0 or cos θ = 1
∴ either sinθ = 0 or cosθ = cosθ …[∵ cos0 = 1]
The general solution of sinθ = 0 is θ = nπ, n ∈ Z and cos θ = cos ∝ is θ = 2nπ ± ∝, where n ∈ Z.
∴ the required general solution is given by
θ = nπ, n ∈ Z or θ = 2nπ ± 0, n ∈ Z
∴ θ = nπ, n ∈ Z or θ = 2nπ, n ∈ Z.

(ii) tan³θ = 3tanθ
Solution:

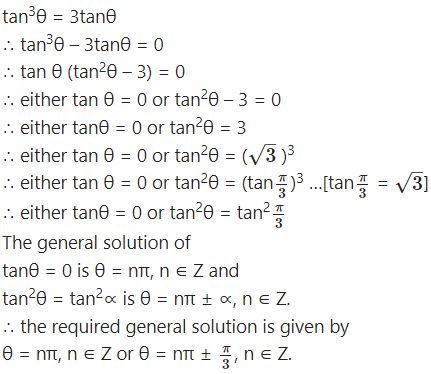
(iii) cosθ + sinθ = 1.
Solution:
cosθ + sinθ = 1

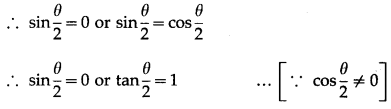
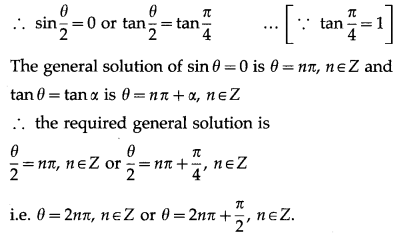
Question 8.
Which of the following equations have solutions ?
(i) cos 2θ = -1
Solution:
cos 2θ = -1
Since -1 ≤ cos θ ≤ 1 for any θ,
cos 2θ = -1 has solution.

(ii) cos²θ = -1
Solution:
cos²θ = -1
This is not possible because cos²θ ≥ 0 for any θ.
∴ cos²θ = -1 does not have any solution.

(iii) 2 sinθ = 3
Solution:
2 sin θ = 3 ∴ sin θ = 3/2
This is not possible because -1 ≤ sin θ ≤ 1 for any θ.
∴ 2 sin θ = 3 does not have any solution.

(iv) 3 tanθ = 5
Solution:
3tanθ = 5 ∴ tanθ = 5/3
This is possible because tan θ is any real number.
∴ 3tanθ = 5 has solution.