Chapter 3 Trigonometry – II Ex 3.1
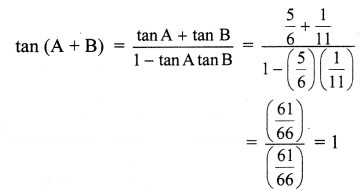
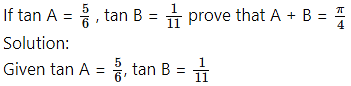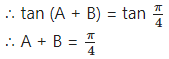Chapter 3 Trigonometry – II Ex 3.1
Question 1.
Find the values of:
i. sin 150°
ü. cos 75°
iii. tan 105°
iv. cot 225°
Solution:
i. sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
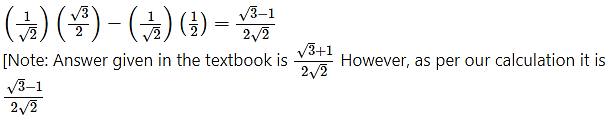
ii. cos 75° = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°
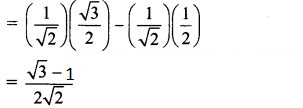
iii. tan 105° = tan (60° +45°)
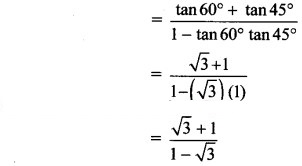
iv. cot 225°
Question 2.
Perove the following:
Solution:
L.H.S
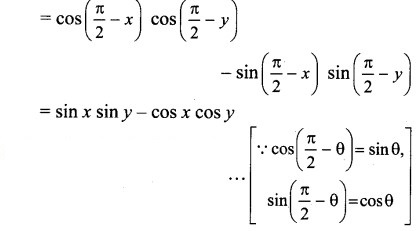
= -(cos x cos y – sin x sin y)
= – cos (x+y)
= R.H.S
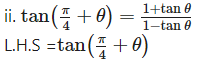
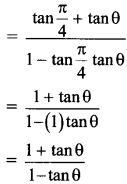
R.H.S.
[Note : The question has been modified.]
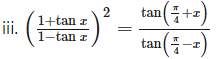
Solution:
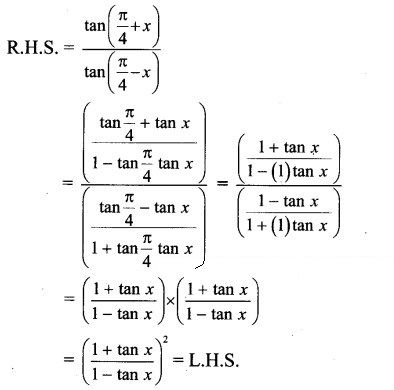
iv. sin [(n+1)A] . sin [(n+2)A] + cos [(n+1)A] . cos [(n+2)A] = cos A
Solution:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let(n+2)Aaand(n+l)Ab …(i)
∴ L.H.S. = cos a. cos b + sin a. sin b
= cos (a — b)
= cos [(n + 2)A — (n + I )A]
…[From (i)]
cos[(n+2 – n – 1)A]
= cos A
= R.H.S.
Solution:
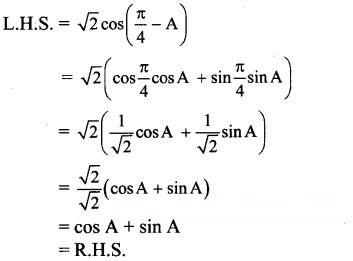
Solution:
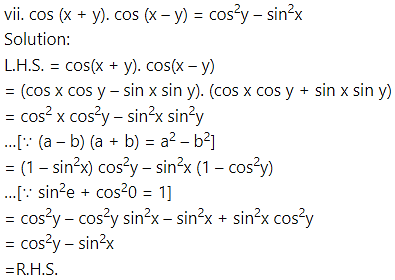
Solution:
ix. tan 8θ – tan 5θ – tan 3θ = tan 8θ tan 5θ tan 3θ
Solution:
Since, 8θ = 5θ + 3θ
∴ tan 8θ = tan (5θ + 3θ)
∴ tan 8θ (1 – tan 5θ.tan 3θ) = tan 5θ + tan 3θ
∴ tan 8θ – tan8θ.tan5θ.tan3θ = tan5θ + tan 3θ
∴ tan 8θ – tan 5θ – tan 3θ = tan 8θ.tan 5θ.tan 3θ
x. tan 50° = tan 40° + 2tan 10°
Solution:
Since, 50° = 10° +40°
∴ tan 50° = tan (10° + 40°)
∴ tan 50° (1 – tan 10° tan 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan 50° = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan (90° – 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° cot 40°
= tan 10° + tan 40° …[∵ tan (90° – θ) = cot θ]
∴ tan 50° – tan 10° tan 40°. = tan 10° + tan 40°
∴ tan 50° – tan 10°. 1 = tan 10° + tan 40°
∴ tan 50° = tan 40° + 2 tan 10°
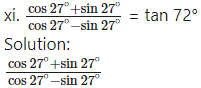
Dividing numerator and cos 27°, we get denominator by cos 27°, we get
= tan (45° + 27°)
= tan 72° = R.H.S
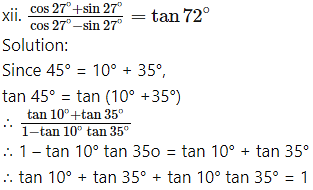
xiii. tan 10° + tan 35° + tan 10°. tan 35° = 1
Solution:
Solution:
Dividing numerator and cos 15°, we get
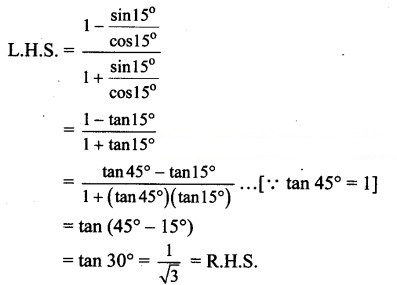
= tan (45° + 15°)
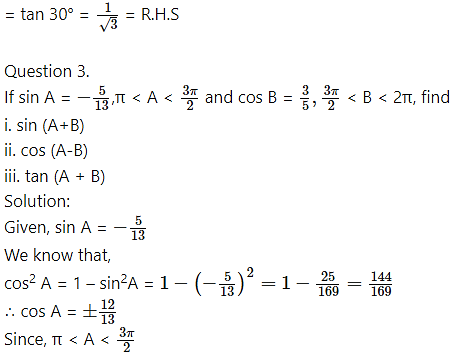
i. sin (A + B) = sin A cos B+cos A sin B
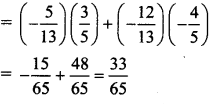
ii. cos (A -B) = cos A cos B + sin A sin B
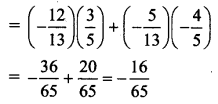
iii.
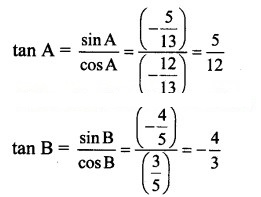
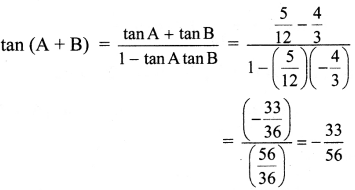
Question 4.
