Chapter 4 Determinants and Matrices Ex 4.6
Chapter 4 Determinants and Matrices Ex 4.6
Question 1.
Evaluate:
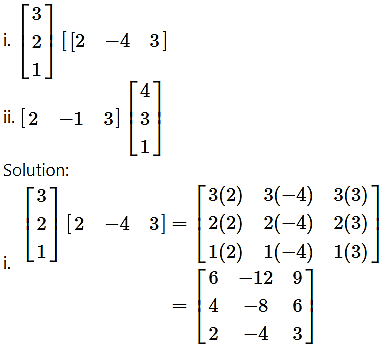
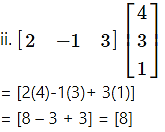
Question 2.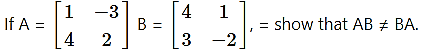
Solution:
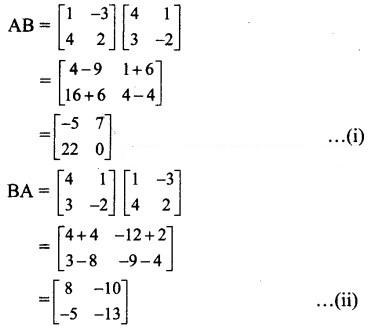
From (i) and (ii), we get
AB ≠ BA
Question 3.
answer.
Solution:
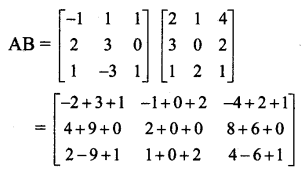

From (i) and (ii), we get
AB ≠ BA
Question 4.
Show that AB = BA, where
Solution:

From (i) and (ii), we get
AB = BA
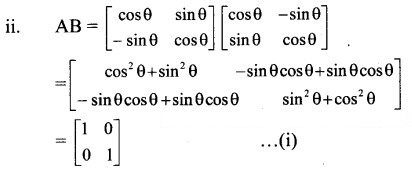
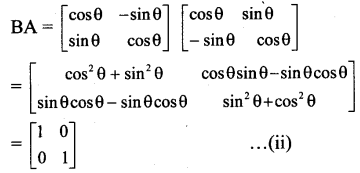
From (i) and (ii), we get
AB = BA
[Note: The question has been modified.]
Question 5.
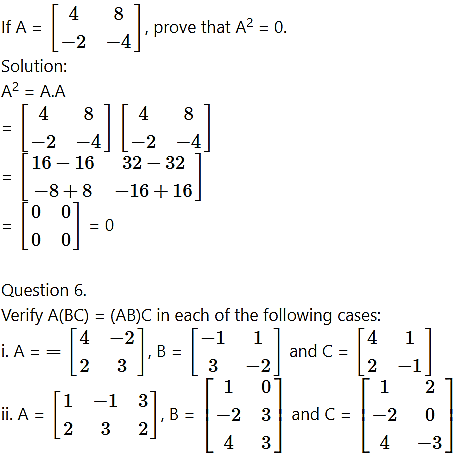
Solution:



From (i) and (ii), we get
A(BC) = (AB)C.
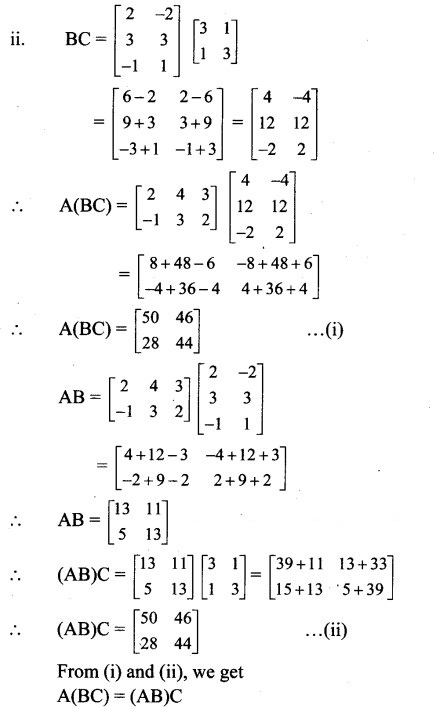
Question 7.
Verify that A(B + C) = AB + AC in each of the following matrices: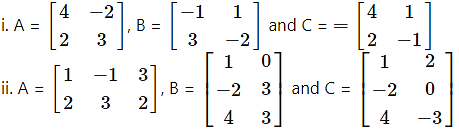
Solution:

From (i) and (ii), we get
A(B + C) = AB + AC.
[Note: The question has been modified.]
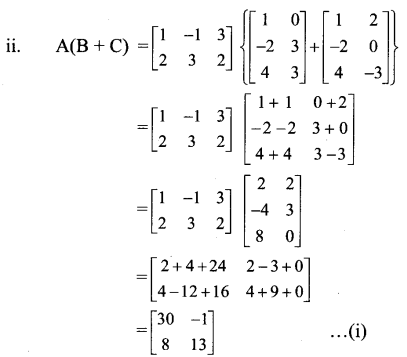

Question 8.
Solution:

Question 9.
Solution:
im
∴ AB is non-singular matrix.
Question 10.
If A = , find the product (A + I)(A – I).
Solution:


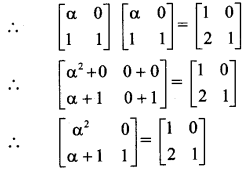
∴ By equality of matrices, we get
= 1 and α + 1 = 2
∴ α = ± 1 and α = 1
∴ α = 1
Question 12.
Solution:
– 4A = A.A – 4A

Question 13.
Solution:
– 8A – kI = O
∴ A.A – 8A – kI = O
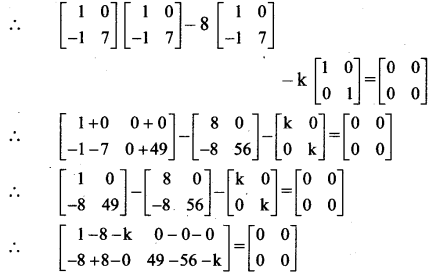
∴ by equality of matrices, we get
1 – 8 – k = 0
∴ k = -7
Question 14.
Solution:
– 5A + 7I = 0 = A.A – 5A + 7I = 0
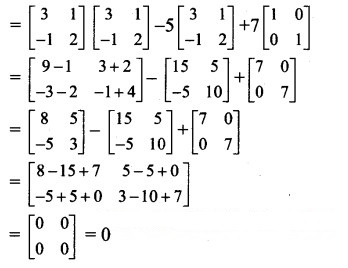
Question 16.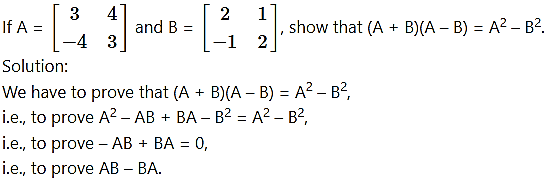
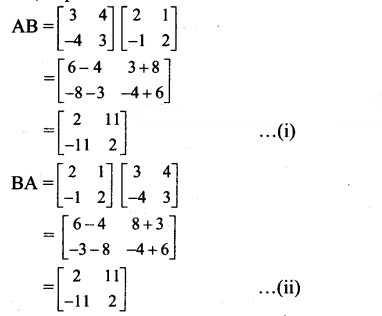
From (i) and (ii), we get AB = BA
Question 17.
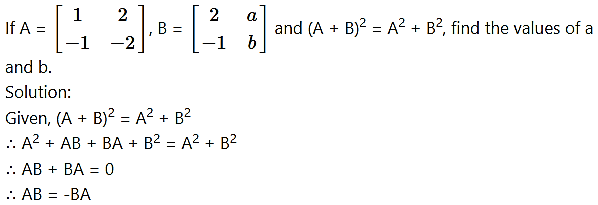
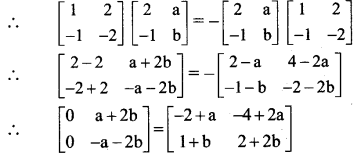
∴ by equality of matrices, we get
– 2 + a = 0 and 1 + b = 0
a = 2 and b = -1
[Note: The question has been modified.]
Question 18.
Find matrix X such that AX = B,
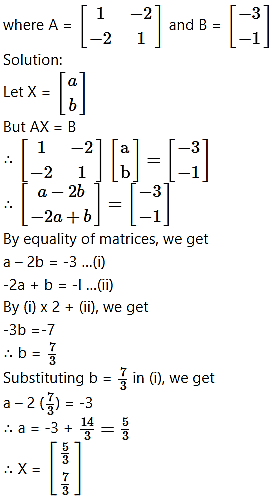
Question 19.![]()
Solution:
= kA – 2I
∴ AA + 2I = kA
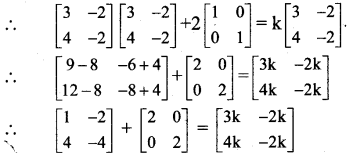
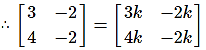
∴ By equality of matrices, we get
3k = 3
∴ k = 1
Question 20.
Solution:
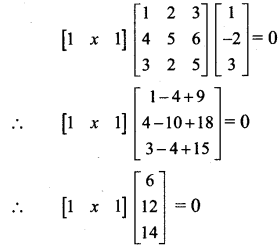
∴ [6 + 12x + 14] =[0]
∴ By equality of matrices, we get
∴ 12x + 20 = 0
∴ 12x =-20
∴ x = -5/3
Question 21.
Solution:
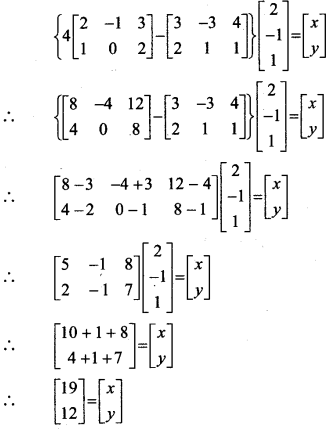
∴ By equality of matrices, we get
x = 19 andy = 12
Question 22.
Find x, y, z if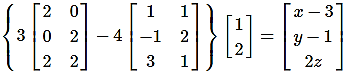
Solution:

∴ By equality of matrices, we get
x – 3 = -6,y – 1 = 0, 2z = -2
∴ x = – 3, y = 1, z = – 1
Question 23.![]()
Solution:
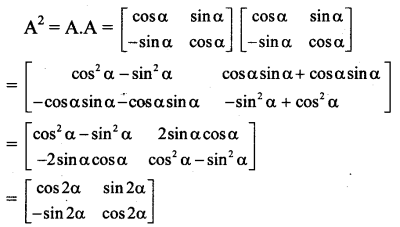
Question 24.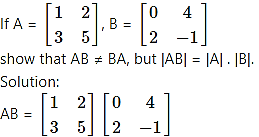

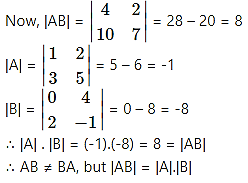
Question 25.
Jay and Ram are two friends in a class. Jay wanted to buy 4 pens and 8 notebooks, Ram wanted to buy 5 pens and 12 notebooks. Both of them went to a shop. The price of a pen and a notebook which they have selected was 6 and ₹ 10. Using matrix multiplication, find the amount required from each one of them.
Solution:
Let A be the matrix of pens and notebooks and B be the matrix of prices of one pen and one notebook.

The total amount required for each one of them is obtained by matrix AB.
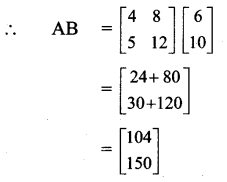
∴ Jay needs ₹ 104 and Ram needs ₹ 150.