Blog

Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4

Chapter 4 Pair of Straight Lines Miscellaneous Exercise 4

I : Choose correct alternatives.
Question 1.
If the equation 4x² + hxy + y² = 0 represents two coincident lines, then h = _________.
(A) ± 2
(B) ± 3
(C) ± 4
(D) ± 5
Solution:
(C) ± 4

Question 2.
If the lines represented by kx² – 3xy + 6y² = 0 are perpendicular to each other then _________.
(A) k = 6
(B) k = -6
(C) k = 3
(D) k = -3
Solution:
(B) k = -6

Question 3.
Auxiliary equation of 2x² + 3xy – 9y² = 0 is _________.
(A) 2m² + 3m – 9 = 0
(B) 9m² – 3m – 2 = 0
(C) 2m² – 3m + 9 = 0
(D) -9m² – 3m + 2 = 0
Solution:
(B) 9m² – 3m – 2 = 0

Question 4.
The difference between the slopes of the lines represented by 3x² – 4xy + y² = 0 is _________.
(A) 2
(B) 1
(C) 3
(D) 4
Solution:
(A) 2

Question 5.
If the two lines ax² +2hxy+ by² = 0 make angles α and β with X-axis, then tan (α + β) = _____.

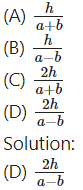
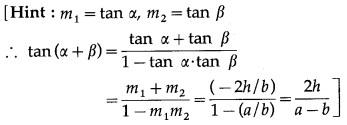
Question 6.

(A) 1 : 2
(B) 2 : 1
(C) 8 : 9
(D) 9 : 8
Solution:
(D) 9 : 8

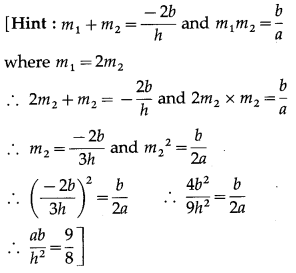
Question 7.
The joint equation of the lines through the origin and perpendicular to the pair of lines 3x² + 4xy – 5y² = 0 is _________.
(A) 5x² + 4xy – 3y² = 0
(B) 3x² + 4xy – 5y² = 0
(C) 3x² – 4xy + 5y² = 0
(D) 5x² + 4xy + 3y² = 0
Solution:
(A) 5x² + 4xy – 3y² = 0

Question 8.
If acute angle between lines ax² + 2hxy + by² = 0 is, π4 then 4h² = _________.
(A) a² + 4ab + b²
(B) a² + 6ab + b²
(C) (a + 2b)(a + 3b)
(D) (a – 2b)(2a + b)
Solution:
(B) a² + 6ab + b²

Question 9.
If the equation 3x² – 8xy + qy² + 2x + 14y + p = 1 represents a pair of perpendicular lines then
the values of p and q are respectively _________.
(A) -3 and -7
(B) -7 and -3
(C) 3 and 7
(D) -7 and 3
Solution:
(B) -7 and -3

Question 10.
The area of triangle formed by the lines x² + 4xy + y² = 0 and x – y – 4 = 0 is _________.

Question 11.
The combined equation of the co-ordinate axes is _________.
(A) x + y = 0
(B) x y = k
(C) xy = 0
(D) x – y = k
Solution:
(C) xy = 0

Question 12.
If h² = ab, then slope of lines ax² + 2hxy + by² = 0 are in the ratio _________.
(A) 1 : 2
(B) 2 : 1
(C) 2 : 3
(D) 1 : 1
Solution:
(D) 1 : 1
[Hint: If h² = ab, then lines are coincident. Therefore slopes of the lines are equal.]

Question 13.
If slope of one of the lines ax² + 2hxy + by² = 0 is 5 times the slope of the other, then 5h² = _________.
(A) ab
(B) 2 ab
(C) 7 ab
(D) 9 ab
Solution:
(D) 9 ab

Question 14.
If distance between lines (x – 2y)² + k(x – 2y) = 0 is 3 units, then k =
(A) ± 3
(B) ± 5√5
(C) 0
(D) ± 3√5
Solution:
(D) ± 3√5
[Hint: (x – 2y)² + k(x – 2y) = 0
∴ (x – 2y)(x – 2y + k) = 0
∴ equations of the lines are x – 2y = 0 and x – 2y + k = 0 which are parallel to each other.

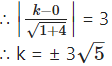
II. Solve the following.
Question 1.
Find the joint equation of lines:
(i) x – y = 0 and x + y = 0
Solution:
The joint equation of the lines x – y = 0 and
x + y = 0 is
(x – y)(x + y) = 0
∴ x² – y² = 0.

(ii) x + y – 3 = 0 and 2x + y – 1 = 0
Solution:
The joint equation of the lines x + y – 3 = 0 and 2x + y – 1 = 0 is
(x + y – 3)(2x + y – 1) = 0
∴ 2x² + xy – x + 2xy + y² – y – 6x – 3y + 3 = 0
∴ 2x² + 3xy + y² – 7x – 4y + 3 = 0.

(iii) Passing through the origin and having slopes 2 and 3.
Solution:
We know that the equation of the line passing through the origin and having slope m is y = mx. Equations of the lines passing through the origin and having slopes 2 and 3 are y = 2x and y = 3x respectively.
i.e. their equations are
2x – y = 0 and 3x – y = 0 respectively.
∴ their joint equation is (2x – y)(3x – y) = 0
∴ 6x² – 2xy – 3xy + y² = 0
∴ 6x² – 5xy + y² = 0.

(iv) Passing through the origin and having inclinations 60° and 120°.
Solution:

(v) Passing through (1, 2) amd parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0
∴ the equations of the lines passing through (1, 2) and parallel to the coordinate axes are x = 1 and y =1
i.e. x – 1 = 0 and y – 2 0
∴ their combined equation is
(x – 1)(y – 2) = 0
∴ x(y – 2) – 1(y – 2) = 0
∴ xy – 2x – y + 2 = 0

(vi) Passing through (3, 2) and parallel to the line x = 2 and y = 3.
Solution:
Equations of the lines passing through (3, 2) and parallel to the lines x = 2 and y = 3 are x = 3 and y = 2.
i.e. x – 3 = 0 and y – 2 = 0
∴ their joint equation is
(x – 3)(y – 2) = 0
∴ xy – 2x – 3y + 6 = 0.

(vii) Passing through (-1, 2) and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0.
Solution:
Let L₁ and L₂ be the lines passing through the origin and perpendicular to the lines x + 2y + 3 = 0 and 3x – 4y – 5 = 0 respectively.

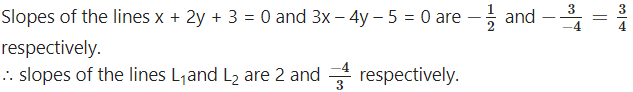
Since the lines L₁ and L₂ pass through the point (-1, 2), their equations are
∴ (y – y₁) = m(x – x₁)
∴ (y – 2) = 2(x + 1)
⇒ y – 1 = 2x + 2
⇒ 2x – y + 4 = 0 and

⇒ 3y – 6 = (-4)(x + 1)
⇒ 3y – 6 = -4x + 4
⇒ 4x + 3y – 6 + 4 = 0
⇒ 4x + 3y – 2 = 0
their combined equation is
∴ (2x – y + 4)(4x + 3y – 2) = 0
∴ 8x² + 6xy – 4x – 4xy – 3y² + 2y + 16x + 12y – 8 = 0
∴ 8x² + 2xy + 12x – 3y² + 14y – 8 = 0

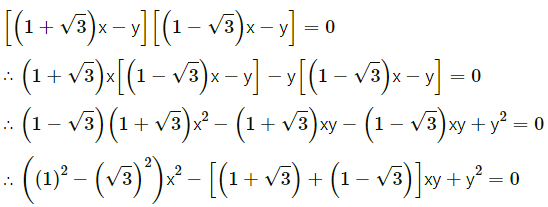
∴ (1 – 3)x² – 2xy + y² = 0
∴ -2x² – 2xy + y² = 0
∴ 2x² + 2xy – y² = 0
This is the required combined equation.

(ix) Which are at a distance of 9 units from the Y – axis.
Solution:
Equations of the lines, which are parallel to the Y-axis and at a distance of 9 units from it, are x = 9 and x = -9
i.e. x – 9 = 0 and x + 9 = 0

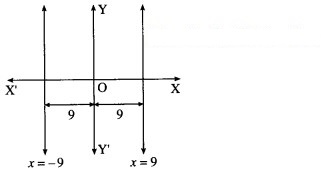
∴ their combined equation is
(x – 9)(x + 9) = 0
∴ x² – 81 = 0.

(x) Passing through the point (3, 2), one of which is parallel to the line x – 2y = 2 and other is perpendicular to the line y = 3.
Solution:

Let L₂ be the line passes through (3, 2) and perpendicular to the line y = 3.
∴ equation of the line L₂ is of the form x = a.
Since L₂ passes through (3, 2), 3 = a
∴ equation of the line L₂ is x = 3, i.e. x – 3 = 0
Hence, the equations of the required lines are
x – 2y + 1 = 0 and x – 3 = 0
∴ their joint equation is
(x – 2y + 1)(x – 3) = 0
∴ x² – 2xy + x – 3x + 6y – 3 = 0
∴ x² – 2xy – 2x + 6y – 3 = 0.

(xi) Passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18.
Solution:
Let L₁ and L₂ be the lines passing through the origin and perpendicular to the lines x + 2y = 19 and 3x + y = 18 respectively.

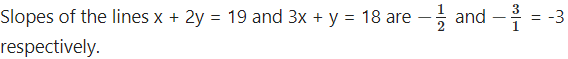
Since the lines L₁ and L₂ pass through the origin, their equations are

i.e. 2x – y = 0 and x – 3y = 0
∴ their combined equation is
(2x – y)(x – 3y) = 0
∴ 2x² – 6xy – xy + 3y² = 0
∴ 2x² – 7xy + 3y² = 0.

Question 2.
Show that each of the following equation represents a pair of lines.
(i) x² + 2xy – y² = 0
Solution:
Comparing the equation x² + 2xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 2, i.e. h = 1 and b = -1
∴ h² – ab = (1)² – 1(-1) = 1 + 1=2 > 0
Since the equation x² + 2xy – y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(ii) 4x² + 4xy + y² = 0
Solution:
Comparing the equation 4x² + 4xy + y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 4, 2h = 4, i.e. h = 2 and b = 1
∴ h² – ab = (2)² – 4(1) = 4 – 4 = 0
Since the equation 4x² + 4xy + y² = 0 is a homogeneous equation of second degree and h² – ab = 0, the given equation represents a pair of lines which are real and coincident.

(iii) x² – y² = 0
Solution:
Comparing the equation x² – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 0, i.e. h = 0 and b = -1
∴ h² – ab = (0)² – 1(-1) = 0 + 1 = 1 > 0
Since the equation x² – y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

(iv) x² + 7xy – 2y² = 0
Solution:

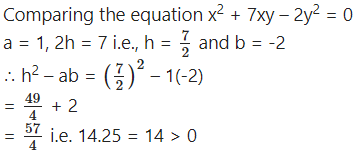
Since the equation x² + 7xy – 2y² = 0 is a homogeneous equation of second degree and h² – ab > 0, the given equation represents a pair of lines which are real and distinct.

Question 3.
Find the separate equations of lines represented by the following equations:
(i) 6x² – 5xy – 6y² = 0
Solution:
6x² – 5xy – 6y² = 0
∴ 6x² – 9xy + 4xy – 6y² = 0
∴ 3x(2x – 3y) + 2y(2x – 3y) = 0
∴ (2x – 3y)(3x + 2y) = 0
∴ the separate equations of the lines are
2x – 3y = 0 and 3x + 2y = 0.

(ii) x² – 4y² = 0
Solution:
x² – 4y² = 0
∴ x² – (2y)² = 0
∴(x – 2y)(x + 2y) = 0
∴ the separate equations of the lines are
x – 2y = 0 and x + 2y = 0.

(iii) 3x² – y² = 0
Solution:

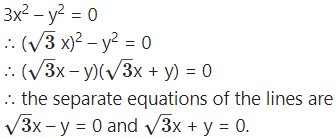
(iv) 2x² + 2xy – y² = 0
Solution:
2x² + 2xy – y² = 0
∴ The auxiliary equation is -m² + 2m + 2 = 0
∴ m² – 2m – 2 = 0

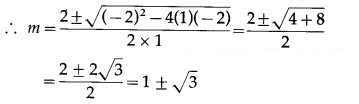
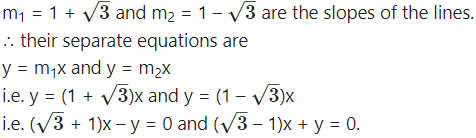
Question 4.
Find the joint equation of the pair of lines through the origin and perpendicular to the lines
given by :
(i) x² + 4xy – 5y² = 0
Solution:
Comparing the equation x² + 4xy – 5y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = 4, b= -5
Let m₁ and m₂ be the slopes of the lines represented by x² + 4xy – 5y² = 0.

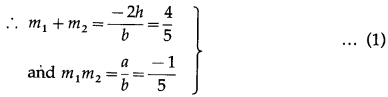
(ii) 2x² – 3xy – 9y² = 0
Solution:

(iii) x² + xy – y² = 0
Solution:

Question 5.
Find k if
(i) The sum of the slopes of the lines given by 3x² + kxy – y² = 0 is zero.
Solution:
Comparing the equation 3x² + kxy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 3, 2h = k, b = -1
Let m₁ and m₂ be the slopes of the lines represented by 3x² + kxy – y² = 0.

Now, m₁ + m₂ = 0 … (Given)
∴ k = 0.

(ii) The sum of slopes of the lines given by 2x² + kxy – 3y² = 0 is equal to their product.
Question is modified.
The sum of slopes of the lines given by x² + kxy – 3y² = 0 is equal to their product.
Solution:
Comparing the equation x² + kxy – 3y² = 0, with ax² + 2hxy + by² = 0, we get,
a = 1, 2h = k, b = -3
Let m₁ and m₂ be the slopes of the lines represented by x² + kxy – 3y² = 0.

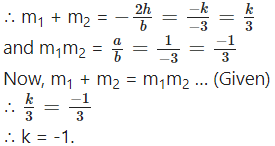
(iii) The slope of one of the lines given by 3x² – 4xy + ky² = 0 is 1.
Solution:
The auxiliary equation of the lines given by 3x² – 4xy + ky² = 0 is km² – 4m + 3 = 0.
Given, slope of one of the lines is 1.
∴ m = 1 is the root of the auxiliary equation km² – 4m + 3 = 0.
∴ k(1)² – 4(1) + 3 = 0
∴ k – 4 + 3 = 0
∴ k = 1.

(iv) One of the lines given by 3x² – kxy + 5y² = 0 is perpendicular to the 5x + 3y = 0.
Solution:

(v) The slope of one of the lines given by 3x² + 4xy + ky² = 0 is three times the other.
Solution:
3x² + 4xy + ky² = 0
∴ divide by x²

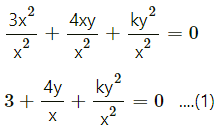
(vi) The slopes of lines given by kx² + 5xy + y² = 0 differ by 1.
Solution:
Comparing the equation kx² + 5xy +y² = 0 with ax² + 2hxy + by²

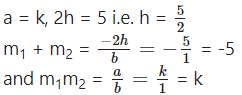
the slope of the line differ by (m₁ – m₂) = 1 …(1)
∴ (m₁ – m₂)² = (m₁ + m₂)² – 4m₁m₂
(m₁ – m₂)² = (-5)² – 4(k)
(m₁ – m₂)² = 25 – 4k
1 = 25 – 4k ..[By (1)]
4k = 24
k = 6

(vii) One of the lines given by 6x² + kxy + y² = 0 is 2x + y = 0.
Solution:
The auxiliary equation of the lines represented by 6x² + kxy + y² = 0 is
m² + km + 6 = 0.
Since one of the line is 2x + y = 0 whose slope is m = -2.
∴ m = -2 is the root of the auxiliary equation m² + km + 6 = 0.
∴ (-2)² + k(-2) + 6 = 0
∴ 4 – 2k + 6 = 0
∴ 2k = 10 ∴ k = 5

Question 6.
Find the joint equation of the pair of lines which bisect angle between the lines given by x² + 3xy + 2y² = 0
Solution:
x² + 3xy + 2y² = 0
∴ x² + 2xy + xy + 2y² = 0
∴ x(x + 2y) + y(x + 2y) = 0
∴ (x + 2y)(x + y) = 0
∴ separate equations of the lines represented by x² + 3xy + 2y² = 0 are x + 2y = 0 and x + y = 0.
Let P (x, y) be any point on one of the angle bisector. Since the points on the angle bisectors are equidistant from both the lines,

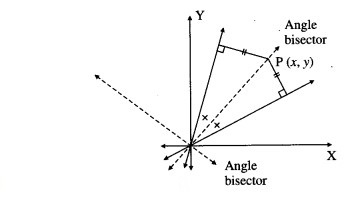
the distance of P (x, y) from the line x + 2y = 0
= the distance of P(x, y) from the line x + y = 0

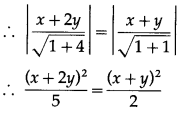
∴ 2(x + 2y)² = 5(x + y)²
∴ 2(x² + 4xy + 4y²) = 5(x² + 2xy + y²)
∴ 2x² + 8xy + 8y² = 5x² + 10xy + 5y²
∴ 3x² + 2xy – 3y² = 0.
This is the required joint equation of the lines which bisect the angles between the lines represented by x² + 3xy + 2y² = 0.

Question 7.
Find the joint equation of the pair of lies through the origin and making equilateral triangle with the line x = 3.
Solution:

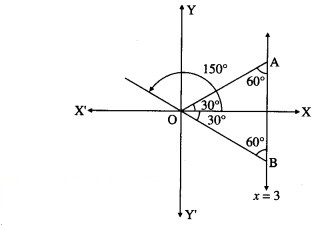
Let OA and OB be the lines through the origin making an angle of 60° with the line x = 3.
∴ OA and OB make an angle of 30° and 150° with the positive direction of X-axis

Question 8.
Show that the lines x² – 4xy + y² = 0 and x + y = 10 contain the sides of an equilateral triangle. Find the area of the triangle.
Solution:
We find the joint equation of the pair of lines OA and OB through origin, each making an angle of 60° with x + y = 10 whose slope is -1.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)

∴ x² – 4xy + y\left(\frac{y}{x}\right) = 0 is the joint equation of the two lines through the origin each making an angle of 60° with x + y = 10
∴ x² – 4xy + y² = 0 and x + y = 10 form a triangle OAB which is equilateral.
Let seg OM ⊥^r line AB whose question is x + y = 10

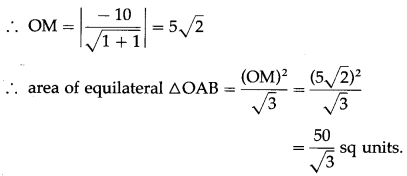
Question 9.
If the slope of one of the lines represented by ax² + 2hxy + by² = 0 is three times the other then prove that 3h² = 4ab.
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.

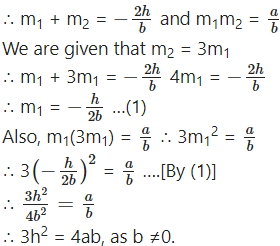
Question 10.
Find the combined equation of the bisectors of the angles between the lines represented by 5x² + 6xy – y² = 0.
Solution:
Comparing the equation 5x² + 6xy – y² = 0 with ax² + 2hxy + by² = 0, we get,
a = 5, 2h = 6, b = -1
Let m₁ and m₂ be the slopes of the lines represented by 5x² + 6xy – y² = 0.

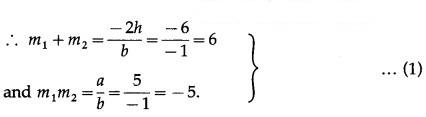
The separate equations of the lines are
y = m₁x and y = m₂x, where m1 ≠ m2
i.e. m₁x – y = 0 and m₁x – y = 0.
Let P (x, y) be any point on one of the bisector of the angles between the lines.
∴ the distance of P from the line m₁x – y = 0 is equal to the distance of P from the line m₂x – y = 0.

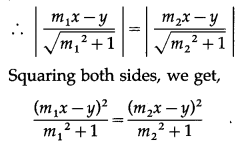
∴ (m₂² + 1)(m₁x – y)² = (m₁² + 1)(m₂x – y)²
∴ (m₂² + 1)(m₁²x² – 2m₁xy + y²) = (m₁² + 1)(m₂²x² – 2m₂xy + y²)
∴ m₁²m₂²x² – 2m₁m₁²y²xy + m₂²y² + m₁²x² – 2m₁²xy + y²
= m₁²m₂²x² – 2m₁²m₂xy + m₁²y² + m₂²x² – 2m₂xy + y²
∴ (m₁² – m₂²)x² + 2m₁m₂(m₁ – m₂)xy – 2(m₁ – m₂)xy – (m₁² – m₂²)y² = 0
Dividing throughout by m₁ – m₂ (≠0), we get,
(m₁ + m₂)x² + 2m₁m₂xy – 2xy – (m₁ + m₂)y² = 0
∴ 6x² – 10xy – 2xy – 6y² = 0 …[By (1)]
∴ 6x² – 12xy – 6y² = 0
∴ x² – 2xy – y² = 0
This is the joint equation of the bisectors of the angles between the lines represented by 5x² + 6xy – y² = 0.

Question 11.
Find a, if the sum of the slopes of the lines represented by ax² + 8xy + 5y² = 0 is twice their product.
Solution :
Comparing the equation ax² + 8xy + 5y² = 0 with ax² + 2hxy + by² = 0,
we get, a = a, 2h = 8, b = 5
Let m₁ and m₂ be the slopes of the lines represented by ax² + 8xy + 5y² = 0.

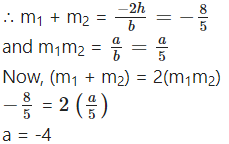
Question 12.
If the line 4x – 5y = 0 coincides with one of the lines given by ax² + 2hxy + by² = 0, then show that 25a + 40h +16b = 0.
Solution :
The auxiliary equation of the lines represented by ax² + 2hxy + by² = 0 is bm² + 2hm + a = 0
Given that 4x – 5y = 0 is one of the lines represented by ax² + 2hxy + by² = 0.

Question 13.
Show that the following equations represent a pair of lines. Find the acute angle between them :
(i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
Solution:
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get,
a = 9, h = -3, b = 1, g = 9, f = -3 and c = 8.

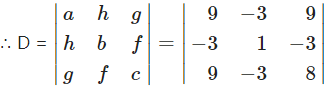
= 9(8 – 9) + 3(-24 + 27) + 9(9 – 9)
= 9(-1) + 3(3) + 9(0)
= -9 + 9 + 0 = 0
and h² – ab = (-3)² – 9(1) = 9 – 9 = 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.

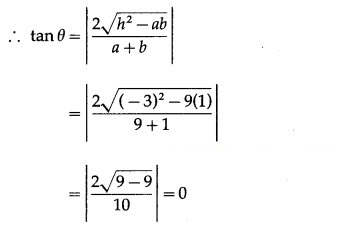
∴ tan θ = tan0°
∴ θ = 0°.

(ii) 2x² + xy – y² + x + 4y – 3 = 0
Solution:
Comparing this equation with
ax² + 2hxy + by² + 2gx + 2fy+ c = 0, we get,
a = 2, h = 1/2, b = -1, g = 1/2, f = 2 and c = -3

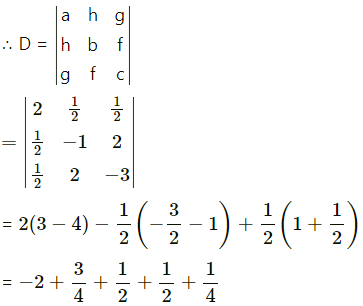
= -2 + 1 + 1
= -2 + 2= 0
∴ the given equation represents a pair of lines.
Let θ be the acute angle between the lines.

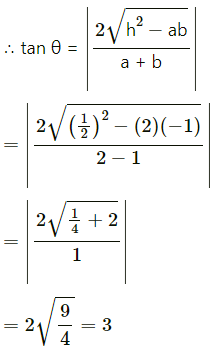
∴ tan θ = tan 3
∴ θ = tan^-1(3)

(iii) (x – 3)² + (x – 3)(y – 4) – 2(y – 4)² = 0.
Solution :

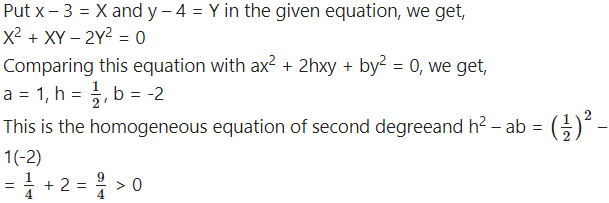
Hence, it represents a pair of lines passing through the new origin (3, 4).
Let θ be the acute angle between the lines.

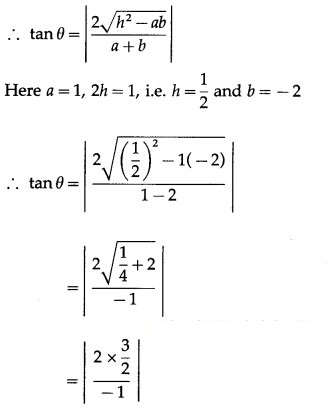
∴ tanθ = 3 ∴ θ = tan^-1(3)

Question 14.
Find the combined equation of pair of lines through the origin each of which makes angle of 60° with the Y-axis.
Solution:

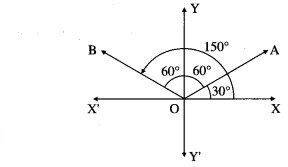
Let OA and OB be the lines through the origin making an angle of 60° with the Y-axis.
Then OA and OB make an angle of 30° and 150° with the positive direction of X-axis.

Question 15.
If lines representedby ax² + 2hxy + by² = 0 make angles of equal measures with the co-ordinate
axes then show that a = ± b.
OR
Show that, one of the lines represented by ax² + 2hxy + by² = 0 will make an angle of the same measure with the X-axis as the other makes with the Y-axis, if a = ± b.
Solution:

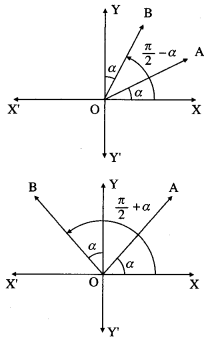
Let OA and OB be the two lines through the origin represented by ax² + 2hxy + by² = 0.
Since these lines make angles of equal measure with the coordinate axes, they make angles ∝ and π/2 – ∝ with the positive direction of X-axis or ∝ and π/2 + ∝ with thepositive direction of X-axis.
∴ slope of the line OA = m₁ = tan ∝
and slope of the line OB = m₂
= tan(π/2 – ∝) or tan(π/2 + ∝)
i.e. m₂ = cot ∝ or m₂ = -cot ∝
∴ m₁m₂ – tan ∝ x cot ∝ = 1
OR m₁m₂ = tan ∝ (-cot ∝) = -1
i.e. m₁m₂ = ± 1
But m₁m₂ = a/b
∴ a/b= ±1 ∴ a = ±b
This is the required condition.

Question 16.
Show that the combined equation of a pair of lines through the origin and each making an angle of ∝ with the line x + y = 0 is x² + 2(sec 2∝) xy + y² = 0.
Solution:
Let OA and OB be the required lines.
Let OA (or OB) has slope m.
∴ its equation is y = mx … (1)
It makes an angle ∝ with x + y = 0 whose slope is -1. m +1

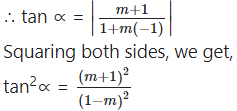
∴ tan²∝(1 – 2m + m²) = m² + 2m + 1
∴ tan²∝ – 2m tan²∝ + m²tan²∝ = m² + 2m + 1
∴ (tan²∝ – 1)m² – 2(1 + tan²∝)m + (tan²∝ – 1) = 0

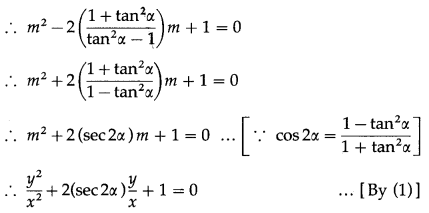
∴ y² + 2xysec2∝ + x² = 0
∴ x² + 2(sec2∝)xy + y² = 0 is the required equation.

Question 17.
Show that the line 3x + 4y+ 5 = 0 and the lines (3x + 4y)² – 3(4x – 3y)² =0 form an equilateral triangle.
Solution:

Let m be the slope of one of the line making an angle of 60° with the line 3x + 4y + 5 = 0. The angle between the lines having slope m and m₁ is 60°.

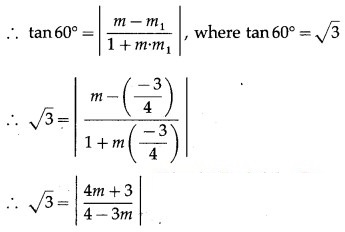
On squaring both sides, we get,

∴ 3 (4 – 3m)² = (4m + 3)²
∴ 3(16 – 24m + 9m²) = 16m² + 24m + 9
∴ 48 – 72m + 27m² = 16m² + 24m + 9
∴ 11m² – 96m + 39 = 0
This is the auxiliary equation of the two lines and their joint equation is obtained by putting m = y/x.
∴ the combined equation of the two lines is

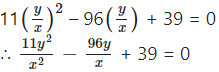
∴ 11y² – 96xy + 39x² = 0
∴ 39x² – 96xy + 11y² = 0.
∴ 39x² – 96xy + 11y² = 0 is the joint equation of the two lines through the origin each making an angle of 60° with the line 3x + 4y + 5 = 0.
The equation 39x² – 96xy + 11y² = 0 can be written as :
-39x² + 96xy – 11y² = 0
i.e., (9x² – 48x²) + (24xy + 72xy) + (16y² – 27y²) = 0
i.e. (9x² + 24xy + 16y²) – (48x² – 72xy + 27y²) = 0
i.e. (9x² + 24xy + 16y²) – 3(16x² – 24xy + 9y²) = 0
i.e. (3x + 4y)² – 3(4x – 3y)² = 0
Hence, the line 3x + 4y + 5 = 0 and the lines
(3x + 4y)² – 3(4x – 3y)² form the sides of an equilateral triangle.

Question 18.
Show that lines x² – 4xy + y² = 0 and x + y = √6 form an equilateral triangle. Find its area and perimeter.
Solution:
x² – 4xy + y² = 0 and x + y = √6 form a triangle OAB which is equilateral.
Let OM be the perpendicular from the origin O to AB whose equation is x + y = √6

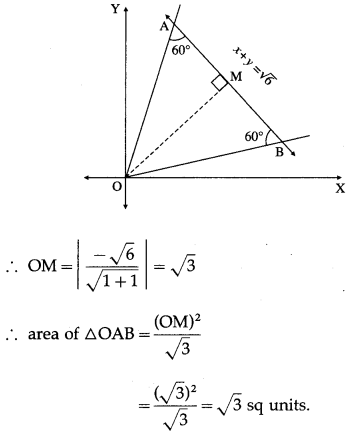
In right angled triangle OAM,
∴ OA = 2
∴ length of the each side of the equilateral triangle OAB = 2 units.
∴ perimeter of ∆ OAB = 3 × length of each side
= 3 × 2 = 6 units.

Question 19.
If the slope of one of the lines given by ax² + 2hxy + by² = 0 is square of the other then show that a²b + ab² + 8h³ = 6abh.
Solution:
Let m be the slope of one of the lines given by ax² + 2hxy + by² = 0.
Then the other line has slope m²

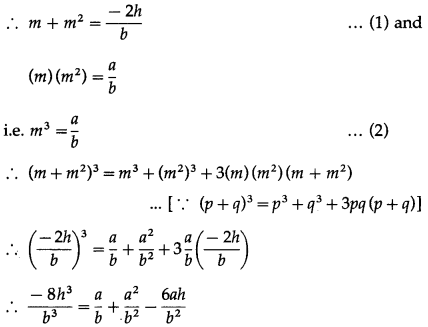
Multiplying by b³, we get,
-8h³ = ab² + a²b – 6abh
∴ a²b + ab² + 8h³ = 6abh
This is the required condition.

Question 20.

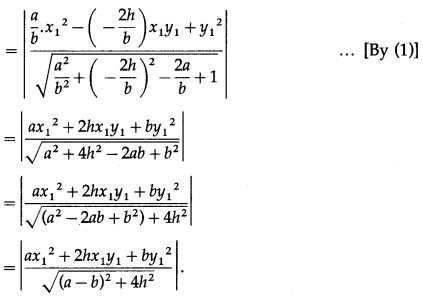
Question 21.
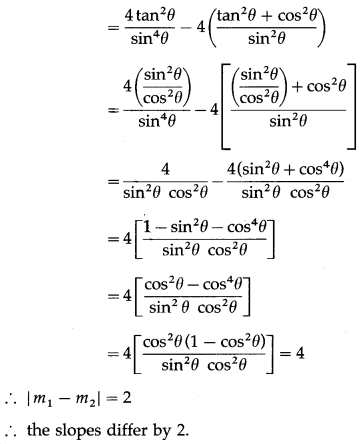
Show that the difference between the slopes of lines given by (tan²θ + cos²θ )x² – 2xytanθ + (sin²θ )y² = 0 is two.
Solution:
Comparing the equation (tan²θ + cos²θ)x² – 2xy tan θ + (sin²θ) y² = 0 with ax² + 2hxy + by² = 0, we get,
a = tan²θ + cos²θ, 2h = -2 tan θ and b = sin2θ
Let m₁ and m₂ be the slopes of the lines represented by the given equation.

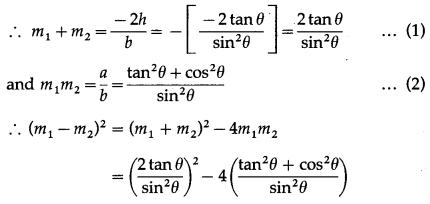
Question 22.
Find the condition that the equation ay² + bxy + ex + dy = 0 may represent a pair of lines.
Solution:
Comparing the equation
ay² + bxy + ex + dy = 0 with
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0, we get,
A = 0, H = b2, B = a,G = e2, F = d2, C = 0
The given equation represents a pair of lines,

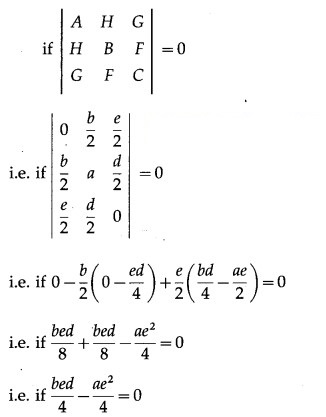
i.e. if bed – ae² = 0
i.e. if e(bd – ae) = 0
i.e. e = 0 or bd – ae = 0
i.e. e = 0 or bd = ae
This is the required condition.

Question 23.
If the lines given by ax² + 2hxy + by² = 0 form an equilateral triangle with the line lx + my = 1 then show that (3a + b)(a + 3b) = 4h².
Solution:
Since the lines ax² + 2hxy + by² = 0 form an equilateral triangle with the line lx + my = 1, the angle between the lines ax² + 2hxy + by² = 0 is 60°.

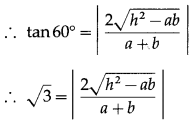
∴ 3(a + b)² = 4(h² – ab)
∴ 3(a² + 2ab + b²) = 4h² – 4ab
∴ 3a² + 6ab + 3b² + 4ab = 4h²
∴ 3a² + 10ab + 3b² = 4h²
∴ 3a² + 9ab + ab + 3b² = 4h²
∴ 3a(a + 3b) + b(a + 3b) = 4h²
∴ (3a + b)(a + 3b) = 4h²
This is the required condition.

Question 24.
If line x + 2 = 0 coincides with one of the lines represented by the equation x² + 2xy + 4y + k = 0 then show that k = -4.
Solution:
One of the lines represented by
x² + 2xy + 4y + k = 0 … (1)
is x + 2 = 0.
Let the other line represented by (1) be ax + by + c = 0.
∴ their combined equation is (x + 2)(ax + by + c) = 0
∴ ax² + bxy + cx + 2ax + 2by + 2c = 0
∴ ax² + bxy + (2a + c)x + 2by + 2c — 0 … (2)
As the equations (1) and (2) are the combined equations of the same two lines, they are identical.
∴ by comparing their corresponding coefficients, we get,

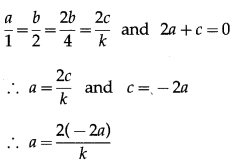
∴ 1 = −4k
∴ k = -4.

Question 25.
Prove that the combined equation of the pair of lines passing through the origin and perpendicular to the lines represented by ax² + 2hxy + by² = 0 is bx² – 2hxy + ay² = 0
Solution:
Let m₁ and m₂ be the slopes of the lines represented by ax² + 2hxy + by² = 0.

Now, required lines are perpendicular to these lines.

Since these lines are passing through the origin, their separate equations are

i.e. m₁y= -x and m₂y = -x
i.e. x + m₁y = 0 and x + m₂y = 0
∴ their combined equation is
(x + m₁y)(x + m₂y) = 0
∴ x² + (m₁ + m₂)xy + m₁m₂y² = 0

∴ bx² – 2hxy + ay² = 0.

Question 26.
If equation ax² – y² + 2y + c = 1 represents a pair of perpendicular lines then find a and c.
Solution:
The given equation represents a pair of lines perpendicular to each other.
∴ coefficient of x² + coefficient of y² = 0
∴ a – 1 = 0 ∴ a = 1
With this value of a, the given equation is
x² – y² + 2y + c – 1 = 0
Comparing this equation with
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0, we get,
A = 1, H = 0, B = -1, G = 0, F = 1, C = c – 1
Since the given equation represents a pair of lines,

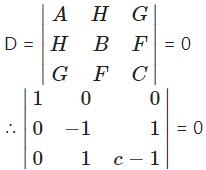
∴ 1(-c + 1 – 1) – 0 + 0 = 0
∴ -c = 0
∴ c = 0.
Hence, a = 1, c = 0.