Blog

Chapter 4 Ratio and Proportion Practice Set 4.5

Chapter 4 Ratio and Proportion Practice Set 4.5

Question 1.
Which number should be subtracted from 12, 16 and 21 so that resultant numbers are in continued proportion?
Solution:
Let the number to be subtracted be x.
∴ (12 – x), (16 – x) and (21 – x) are in continued proportion.

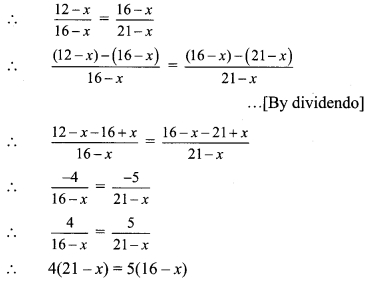
∴ 84 – 4x = 80 – 5x
∴ 5x – 4x = 80 – 84
∴ x = -4
∴ -4 should be subtracted from 12,16 and 21 so that the resultant numbers in continued proportion.

Question 2.
If (28 – x) is the mean proportional of (23 – x) and (19 – x), then find the value ofx.
Solution:
(28 – x) is the mean proportional of (23 – x) and (19-x). …[Given]

∴ -5(19 – x) = 9(28 – x)
∴ -95 + 5x = 252 – 9x
∴ 5x + 9x = 252 + 95
∴ 14x = 347

Question 3.
Three numbers are in continued proportion, whose mean proportional is 12 and the sum of the remaining two numbers is 26, then find these numbers.
Solution:
Let the first number be x.
∴ Third number = 26 – x
12 is the mean proportional of x and (26 – x).

∴ x(26 – x) = 12 x 12
∴ 26x – x² = 144
∴ x² – 26x + 144 = 0
∴ x² – 18x – 8x + 144 = 0
∴ x(x – 18) – 8(x – 18) = 0
∴ (x – 18) (x – 8) = 0
∴ x = 18 or x = 8
∴ Third number = 26 – x = 26 – 18 = 8 or 26 – x = 26 – 8 = 18
∴ The numbers are 18, 12, 8 or 8, 12, 18.

Question 4.
If (a + b + c)(a – b + c) = a² + b² + c², show that a, b, c are in continued proportion.
Solution:
(a + b + c)(a – b + c) = a² + b² + c² …[Given]
∴ a(a – b + c) + b(a – b + c) + c(a – b + c) = a2 + b2 + c2
∴ a² – ab + ac + ab – b² + be + ac – be + c² = a² + b² + c²
∴ a² + 2ac – b² + c² = a² + b² + c²
∴ 2ac – b² = b²
∴ 2ac = 2b²
∴ ac = b²
∴ b² = ac
∴ a, b, c are in continued proportion.

Question 5.
If a/b = b/c and a, b, c > 0, then show that,
i. (a + b + c)(b – c) = ab – c²
ii. (a² + b²)(b² + c²) = (ab + be)²

∴ b = ck
∴ a = bk =(ck)k
∴ a = ck² …(ii)

i. (a + b + c)(b – c) = ab – c²
L.H.S = (a + b + c) (b – c)
= [ck² + ck + c] [ck – c] … [From (i) and (ii)]
= c(k² + k + 1) c (k – 1)
= c² (k² + k + 1) (k – 1)
R.H.S = ab – c²
= (ck²) (ck) – c² … [From (i) and (ii)]
= c²k³ – c²
= c²(k³ – 1)
= c² (k – 1) (k² + k + 1) … [a³ – b³ = (a – b) (a² + ab + b²]
∴ L.H.S = R.H.S
∴ (a + b + c) (b – c) = ab – c²

ii. (a² + b²)(b² + c²) = (ab + bc)²
b = ck; a = ck²
L.H.S = (a² + b²) (b² + c²)
= [(ck²) + (ck)²] [(ck)² + c²] … [From (i) and (ii)]
= [c²k⁴ + c²k²] [c²k² + c²]
= c²k² (k² + 1) c² (k² + 1)
= c4k² (k² + 1)²
R.H.S = (ab + bc)²
= [(ck²) (ck) + (ck)c]² …[From (i) and (ii)]
= [c²k³ + c²k]²
= [c²k (k² + 1)]2 = c⁴(k² + 1)²
∴ L.H.S = R.H.S
∴ (a² + b²) (b² + c²) = (ab + bc)²

Question 6. Find mean proportional of
Solution: