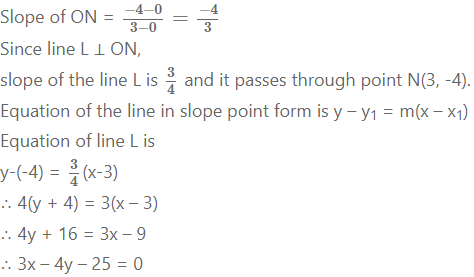Chapter 5 Straight Line Ex 5.3
Chapter 5 Straight Line Ex 5.3
Question 1.
Write the equation of the line:
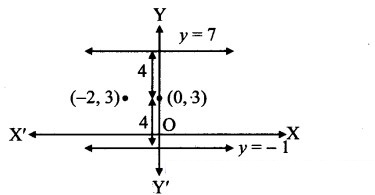
i. parallel to the X-axis and at a distance of 5 units from it and above it.
ii. parallel to the Y-axis and at a distance of 5 units from it and to the left of it.
iii. parallel to the X-axis and at a distance of 4 units from the point (- 2,3).
Solution:
i. Equation of a line parallel to X-axis is y = k. Since the line is at a distance of 5 units above X-axis, k = 5
∴ The equation of the required line is y = 5.
ii. Equation of a line parallel to Y-axis is x = h. Since the line is at a distance of 5 units to the left of Y-axis, h = -5
∴ The equation of the required line is x = -5.
[Note: Answer given in the textbook is ‘y = -5
However, we found that ‘x = – 5’.]
iii. Equation of a line parallel to the X-axis is of the form y = k (k > 0 or k < 0).
Since the line is at a distance of 4 units from the point (- 2, 3),
k = 4 + 3 = 7 or k = 3- 4 = -1
∴ The equation of the required line is y = 1 or y = – 1.
Question 2.
Obtain the equation of the line:
i. parallel to the X-axis and making an intercept of 3 units on the Y-axis.
ii. parallel to the Y-axis and making an intercept of 4 units on the X-axis.
Solution:
i. Equation of a line parallel to X-axis with y-intercept ‘k’ isy = k.
Here, y-intercept = 3
∴ The equation of the required line is y = 3.
ii. Equation of a line parallel to Y-axis with x-intercept ‘h’ is x = h.
Here, x-intercept = 4
∴ The equation of the required line is x = 4.
Question 3.
Obtain the equation of the line containing the point:
i. A(2, – 3) and parallel to the Y-axis.
ii. B(4, – 3) and parallel to the X-axis.
Solution:
i. Equation of a line parallel to Y-axis is of the form x = h.
Since the line passes through A(2, – 3), h = 2
∴ The equation of the required line is x = 2.
ii. Equation of a line parallel to X-axis is of the formy = k.
Since the line passes through B(4, – 3), k = -3
∴ The equation of the required line is y = – 3.
Question 4.
Find the equation of the line:
i. passing through the points A(2, 0) and B(3,4)
ii. passing through the points P(2, 1) and Q(2,-1)
Solution:
ii. The required line passes through the points P(2, 1) and Q(2,-1).
Since both the given points have same
x co-ordinates i.e. 2,
the given points lie on the line x = 2.
∴ The equation of the required line is x = 2.
Question 5.
Find the equation of the line:
i. containing the origin and having inclination 60°.
ii. passing through the origin and parallel to AB, where A is (2,4) and B is (1,7).
iii. having slope 1/2 and containing the point (3, -2)
iv. containing the point A(3, 5) and having slope 2/3
v. containing the point A(4, 3) and having inclination 120°.
vi. passing through the origin and which bisects the portion of the line 3JC + y = 6 intercepted between the co-ordinate axes.
Solution:
i. Given, Inclination of line = θ = 60°
Slope of the line (m) = tan θ = tan 60°
= √3
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
.‘. The equation of the required line is y = √3 x
ii. Given, A (2, 4) and B (1, 7)
Since the required line is parallel to line AB, slope of required line (m) = slope of AB
∴ m = – 3 and the required line passes through the origin.
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is y = – 3x
iii. Given, slope(m) = 1/2 and the line passes through (3, – 2).
Equation of the line in slope point form is
y-= m(x-)
∴ The equation of the required line is
[y-(- 2)]=1/2 (x-3)
∴ 2(y + 2)=x – 3
∴ 2y + 4 = x – 3
∴ x – 2y – 7 = 0
iv. Given, slope(m) = 2/3 and the line passes through (3, 5).
Equation of the line in slope point form is y- = m(x -)
∴ The equation of the required line is y – 5 = 2/3 (x-3)
∴ 3 (y – 5) = 2 (x – 3)
∴ 3y – 15 = 2x – 6
∴ 2x – 3y + 9 = 0
v. Given, Inclination of line = θ = 120°
Slope of the line (m) = tan θ = tan 120°
= tan (90° + 30°)
= – cot 30°
= – √3
and the line passes through A(4, 3).
Equation of the line in slope point form is y- = m(x -)
∴ The equation of the required line is
y- 3 = –√3(x-4)
∴ y – 3 = –√3 x + 4√3
∴ √3x + y – 3 -4√3 = 0
vi.
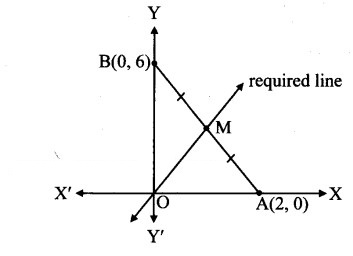
Alternate Method:
Given equation of the line is 3x + y = 6 …(i)
Substitute y = 0 in (i) to get a point on X-axis.
∴ 3x + 0 = 6
∴ x = 2
Substitute x = 0 in (i) to get a point on Y-axis.
∴ 3(0) + 7 = 6
∴ y = 6
∴ The line 3x + y = 6 intersects the X-axis and Y-axis at A(2,0) and B(0,6) respectively.
Let M be the midpoint of AB.
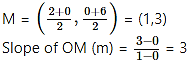
Equation of OM is of the formy = mx.
∴ The equation of the required line is y = 3x
∴ 3x – y = 0
Question 6.
Line y = mx + c passes through the points A(2,1) and B(3,2). Determine m and c.
Solution:
Alternate Method:
Points A(2, 1) and B(3, 2) lie on the line y = mx + c.
∴ They must satisfy the equation.
∴ 2m + c = 1 …(i)
and 3m + c = 2 …(ii)
equation (ii) – equation (i) gives m = 1
Substituting m = 1 in (i), we get 2(1) + c = 1
∴ c = 1 – 2 = – 1
Question 7.
Find the equation of the line having inclination 135° and making x-intercept 7.
Solution:
Given, Inclination of line = 0 = 135°
∴ Slope of the line (m) = tan 0 = tan 135°
= tan (90° + 45°)
= – cot 45° = – 1 x-intercept of the required line is 7.
∴ The line passes through (7, 0).
Equation of the line in slope point form is y – = m(x – )
∴ The equation of the required line is y — 0 = – 1 (x – 7)
∴ y = -x + 7
∴ x + y – 7 = 0
Question 8.
The vertices of a triangle are A(3, 4), B(2, 0) and C(- 1, 6). Find the equations of the lines containing
i. side BC
ii. the median AD
iii. the midpoints of sides AB and BC.
Solution:
Vertices of AABC are A(3, 4), B(2, 0) and C(- 1, 6).
i. Equation of the line in two point form is
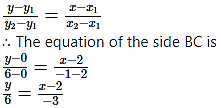
∴ – 3y = 6x – 12
∴ 6x + 3y – 12 = 0
∴ 2x + y – 4 = 0
ii. Let D be the midpoint of side BC.
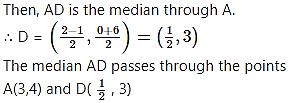
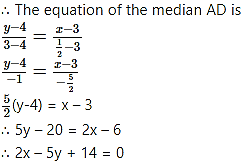
iii. Let D and E be the midpoints of side AB and side BC respectively.
The equation of the line DE is
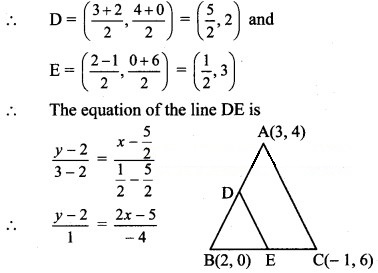
∴ -4(y-2) = 2x-5
∴ 2x + 4y – 13 = 0
Question 9.
where x-intercept = a, y-intercept = b
∴ x-intercept = – 6 and y-intercept = 4
Question 10.
Find equations of the line which contains the point A(l, 3) and the sum of whose intercepts on the co-ordinate axes is zero.
Solution:
Question 11.
Find equations of the line containing the point A(3, 4) and making equal intercepts on the co-ordinate axes.
Solution:
Question 12.
Find the equations of the altitudes of the triangle whose vertices are A(2, 5), B(6, – 1 ) and C(- 4, – 3).
Solution:
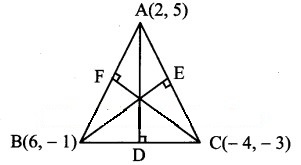
A(2, 5), B(6, – 1), C(- 4, – 3) are the vertices of ∆ABC.
Let AD, BE and CF be the altitudes through the vertices A, B and C respectively of ∆ABC.
∴ Slope of AD = -5 …[∵AD ⊥ BC]
Since altitude AD passes through (2, 5) and has slope – 5,
equation of the altitude AD is y – 5 = -5 (x – 2)
∴ y – 5 = – 5x + 10
∴ 5x +y -15 = 0
Question 13.
Find the equations of perpendicular bisectors of sides of the triangle whose vertices are P(-1, 8), Q(4, – 2) and R(- 5, – 3).
Solution:
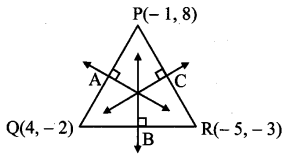
Let A, B and C be the midpoints of sides PQ, QR and PR respectively of APQR.
A is the midpoint of side PQ.
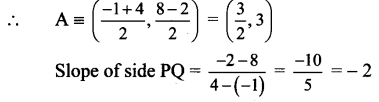
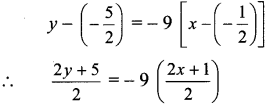
∴ 2y + 5 = -18x – 9
∴ 18x + 2y + 14 = 0
∴ 9x + y + 7 = 0
C is the midpoint of side PR.
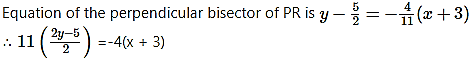
∴ 11(2y – 5) = – 8 (x + 3)
∴ 22y – 55 = – 8x – 24
∴ 8x + 22y -31 = 0
Question 14.
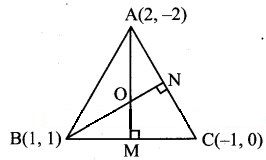
Find the co-ordinates of the orthocentre of the triangle whose vertices are A(2, – 2), B(l, 1) and C(-1,0).
Solution:
Let O be the orthocentre of AABC.
Let AM and BN be the altitudes of sides BC and AC respectively.
Slope of AM = -2 ,..[∵ AM ⊥ BC]
Since AM passes through (2, – 2) and has slope -2,
equation of the altitude AM is y – (- 2) = – 2 (x – 2)
∴ y + 2 = -2x + 4
∴ 2x + y – 2 = 0 …(i)
Question 15.
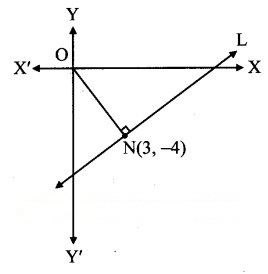
N(3, – 4) is the foot of the perpendicular drawn from the origin to line L. Find the equation of line L.
Solution:
