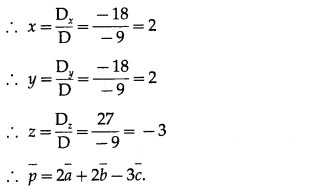Chapter 5 Vectors Ex 5.1
Chapter 5 Vectors Ex 5.1
Question 1.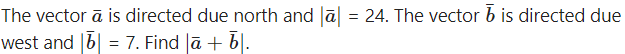
Solution:
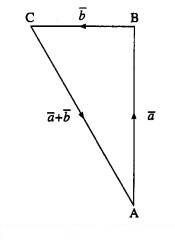
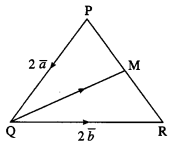
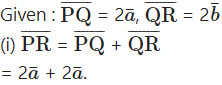
Question 3.
Solution:
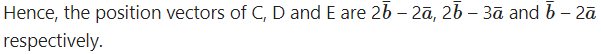
Question 4.
If ABCDEF is a regular hexagon, show 
Solution:
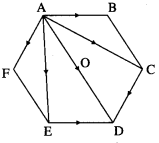
ABCDEF is a regular hexagon.
∴ by the triangle law of addition of vectors,
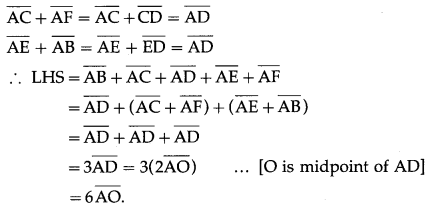
Question 5.
Question 6.
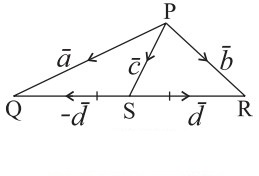
Solution:
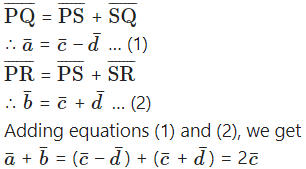
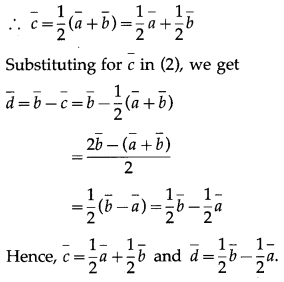
Question 7.
Find the distance from (4, -2, 6) to each of the following :
(a) The XY-plane
Solution:
Let the point A be (4, -2, 6).
Then,
The distance of A from XY-plane = |z| = 6
(b) The YZ-plane
Solution:
The distance of A from YZ-plane = |x| = 4
(c) The XZ-plane
Solution:
The distance of A from ZX-plane = |y| = 2
(d) The X-axis
Solution:
The distance of A from X-axis
(e) The Y-axis
Solution:
The distance of A from Y-axis
(f) The Z-axis
Solution:
The distance of A from Z-axis
Question 8.
Find the coordinates of the point which is located :
(a) Three units behind the YZ-plane, four units to the right of the XZ-plane and five units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located 3 units behind the YZ- j plane, 4 units to the right of XZ-plane and 5 units , above the XY-plane,
x = -3, y = 4 and z = 5
Hence, coordinates of the required point are (-3, 4, 5)
(b) In the YZ-plane, one unit to the right of the XZ-plane and six units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located in the YZ plane, x = 0. Also, the point is one unit to the right of XZ-plane and six units above the XY-plane.
∴ y = 1, z = 6.
Hence, coordinates of the required point are (0, 1, 6).
Question 9.
Find the area of the triangle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Solution:
Let A = (1, 1, 0), B = (1, 0, 1), C = (0, 1, 1)
Question 10.
Question 11.
Show that the following points are collinear :
(i) A (3, 2, -4), B (9, 8, -10), C (-2, -3, 1).
Solution:
A = (3, 2, -4), B = (9, 8, -10) and C = (-2, -3, 1) respectively.
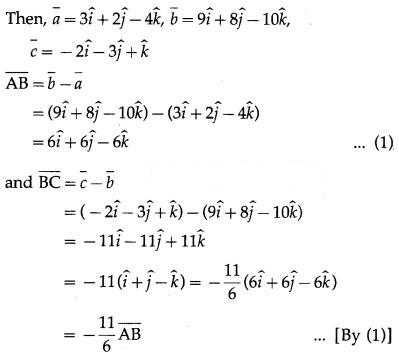
(ii) P (4, 5, 2), Q (3, 2, 4), R (5, 8, 0).
Solution:
P = (4, 5, 2), Q = (3, 2, 4), R = (5, 8, 0) respectively.
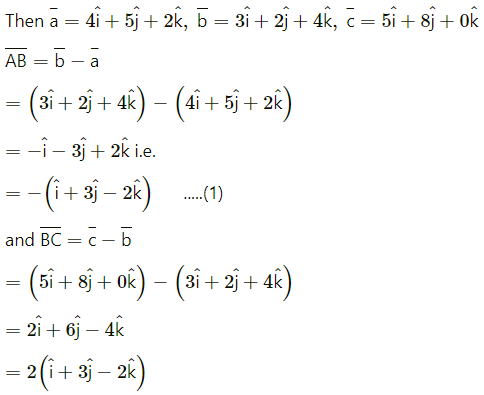
Question 12.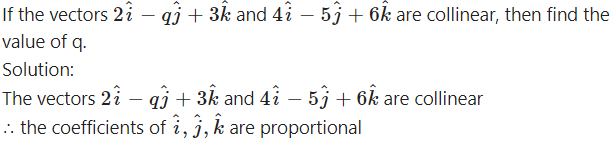
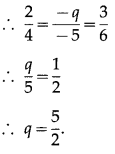
Question 13.
Are the four points A(1, -1, 1), B(-1, 1, 1), C(1, 1, 1) and D(2, -3, 4) coplanar? Justify your answer.
Solution:
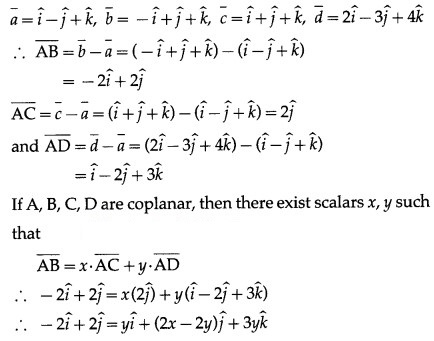
By equality of vectors,
y = -2 ….(1)
2x – 2y = 2 … (2)
3y = 0 … (3)
From (1), y = -2
From (3), y = 0 This is not possible.
Hence, the points A, B, C, D are not coplanar.
Question 14.
Solution:
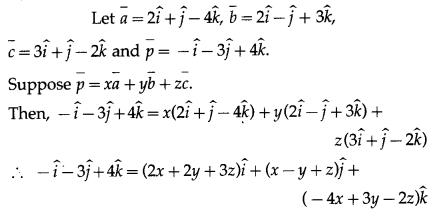
By equality of vectors,
2x + 2y + 3 = -1
x – y + z = -3
-4x + 3y – 2z = 4
We have to solve these equations by using Cramer’s Rule
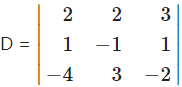
= 2(2 – 3) – 2(-2 + 4) + 3(3 – 4)
= -2 – 4 – 3 = -9 ≠ 0
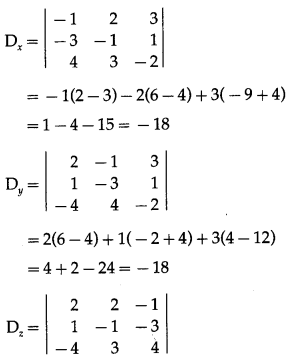
= 2(-4 + 9) – 2(4 – 12) – 1(3 – 4)
= 10 + 16 + 1 = 27
