Blog

Chapter 5 Vectors Ex 5.2

Chapter 5 Vectors Ex 5.2

Question 1.

(ii) externally.
Solution:
If R(r¯) divides the line segment joining P and Q externally in the ratio 3 : 2, by section formula for external division,

∴ coordinates of R = (-19, 8, -21).

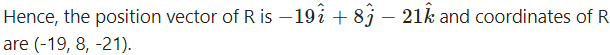
Question 2.
Find the position vector of midpoint M joining the points L (7, -6, 12) and N (5, 4, -2).
Solution:


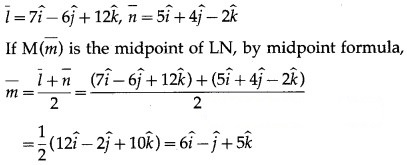
∴ coordinates of M = (6, -1, 5).

Question 3.
If the points A(3, 0, p), B (-1, q, 3) and C(-3, 3, 0) are collinear, then find
(i) The ratio in which the point C divides the line segment AB.
Solution:

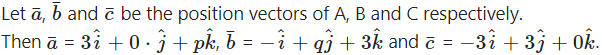
As the points A, B, C are collinear, suppose the point C divides line segment AB in the ratio λ : 1.
∴ by the section formula,

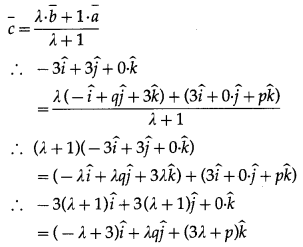
By equality of vectors, we have,
-3(λ + 1) = -λ + 3 … (1)
3(λ + 1 ) = λ q … (2)
0 = 3λ + p … (3)
From equation (1), -3λ – 3 = -λ + 3
∴ -2λ = 6 ∴ λ = -3
∴ C divides segment AB externally in the ratio 3 : 1.

(ii) The values of p and q.
Solution:
Putting λ = -3 in equation (2), we get
3(-3 + 1) = -3q
∴ -6 = -3q ∴ q = 2
Also, putting λ = -3 in equation (3), we get
0 = -9 + p ∴ p = 9
Hence p = 9 and q = 2.

Question 4.


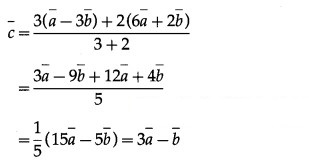
Hence, the position vector of C is 3a¯ – b¯.

Question 5.
Prove that the line segments joining mid-point of adjacent sides of a quadrilateral form a parallelogram.
Solution:
Let ABCD be a quadrilateral and P, Q, R, S be the midpoints of the sides AB, BC, CD and DA respectively.

Since P, Q, R and S are the midpoints of the sides AB, BC, CD and DA respectively,


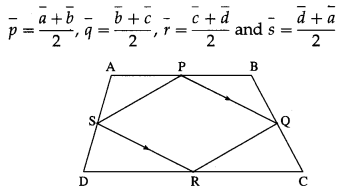
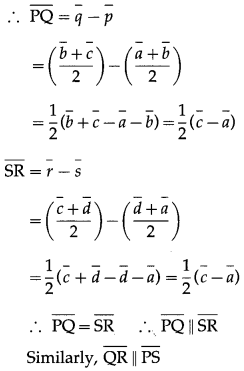
∴ □PQRS is a parallelogram.

Question 6.
D and E divide sides BC and CA of a triangle ABC in the ratio 2 : 3 respectively. Find the position vector of the point of intersection of AD and BE and the ratio in which this point divides AD and BE.
Solution:

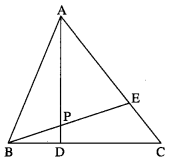
Let AD and BE intersect at P.

D and E divide segments BC and CA internally in the ratio 2 : 3.
By the section formula for internal division,

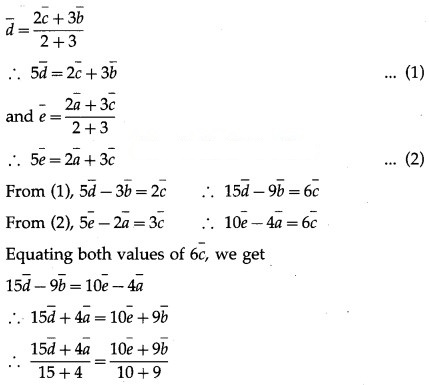
LHS is the position vector of the point which divides segment AD internally in the ratio 15 : 4.
RHS is the position vector of the point which divides segment BE internally in the ratio 10 : 9.
But P is the point of intersection of AD and BE.
∴ P divides AD internally in the ratio 15 : 4 and P divides BE internally in the ratio 10 : 9.
Hence, the position vector of the point of interaction of

Question 7.
Prove that a quadrilateral is a parallelogram if and only if its diagonals bisect each other.
Solution:
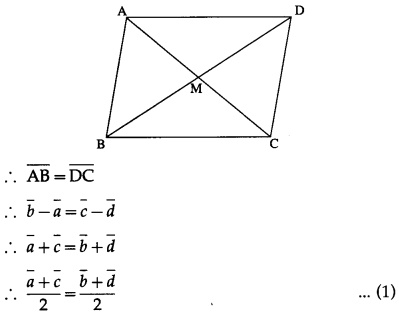
Let a¯, b¯, c¯ and d¯ be respectively the position vectors of the vertices A, B, C and D of the parallelogram ABCD. Then AB = DC and side AB || side DC.

Question 8.
Prove that the median of a trapezium is parallel to the parallel sides of the trapezium and its length is half the sum of parallel sides.
Solution:



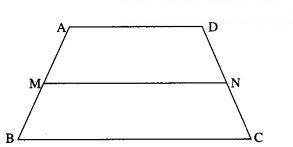
Then seg MN is the median of the trapezium.
By the midpoint formula,

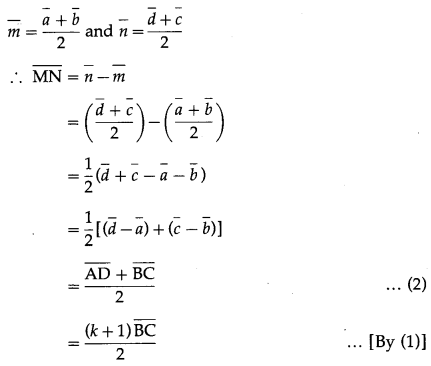
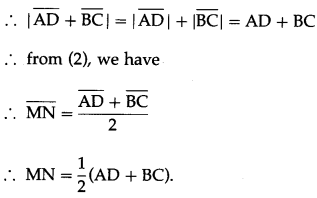
Question 9.
If two of the vertices of the triangle are A(3, 1, 4) and B(-4, 5, -3) and the centroid of a triangle is G(-1, 2, 1), then find the coordinates of the third vertex C of the triangle.
Solution:


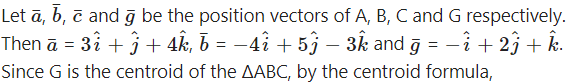
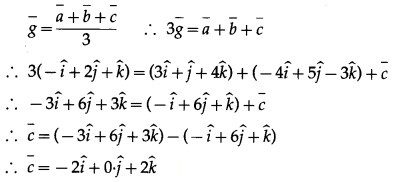
∴ the coordinates of third vertex C are (-2, 0, 2).

Question 10.
In ∆OAB, E is the mid-point of OB and D is the point on AB such that AD : DB = 2 : 1.
If OD and AE intersect at P, then determine the ratio OP : PD using vector methods.
Solution:


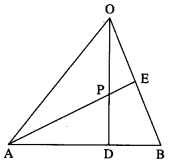
∵ AD : DB = 2 : 1.
∴ D divides AB internally in the ratio 2 : 1.
Using section formula for internal division, we get

LHS is the position vector of the point which divides OD internally in the ratio 3 : 2.
RHS is the position vector of the point which divides AE internally in the ratio 4 : 1.
But OD and AE intersect at P
∴ P divides OD internally in the ratio 3 : 2.
Hence, OP : PD = 3 : 2.

Question 11.
If the centroid of a tetrahedron OABC is (1, 2, -1) where A = (a, 2, 3), B = (1, b, 2), C = (2, 1, c) respectively, find the distance of P (a, b, c) from the origin.
Solution:
Let G = (1, 2, -1) be the centroid of the tetrahedron OABC.


By equality of vectors
a + 3 = 4, b + 3 = 8, c + 5= -4
∴ a = 1, b = 5, c = -9
∴ P = (a, b, c) = (1, 5, -9)

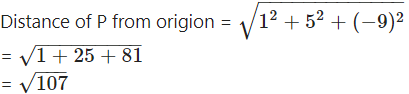
Question 12.
Find the centroid of tetrahedron with vertices K(5, -7, 0), L(1, 5, 3), M(4, -6, 3), N(6, -4, 2) ?
Solution:


Hence, the centroid of the tetrahedron is G = (4, -3, 2).