Blog

Chapter 5 Vectors Miscellaneous Exercise 5

Chapter 5 Vectors Miscellaneous Exercise 5

I) Select the correct option from the given alternatives :
Question 1.

(A) 24
(B) -24
(C) 0
(D) 48
Solution:
(C) 0

Question 2.


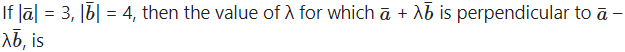
Solution:

Question 3.
If sum of two unit vectors is itself a unit vector, then the magnitude of their difference is
(A) √2
(B) √3
(C) 1
(D) 2
Solution:
(B) √3

Question 4.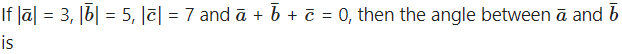


Solution:

Question 5.
The volume of tetrahedron whose vertices are (1, -6, 10), (-1, -3, 7), (5, -1, λ) and (7, -4, 7) is 11 cu. units then the value of λ is
(A) 7
(B) π/3
(C) 1
(D) 5
Solution:
(A) 7

Question 6.
If α, β, γ are direction angles of a line and α = 60º, β = 45º, the γ =
(A) 30º or 90º
(B) 45º or 60º
(C) 90º or 30º
(D) 60º or 120º
Solution:
(D) 60º or 120º

Question 7.
The distance of the point (3, 4, 5) from Y- axis is
(A) 3
(B) 5
(C) √34
(D) √41
Solution:
(C) √34

Question 8.
The line joining the points (-2, 1, -8) and (a, b, c) is parallel to the line whose direction ratios are 6, 2, 3. The value of a, b, c are
(A) 4, 3, -5

(C) 10, 5, -2
(D) 3, 5, 11
Solution:
(A) 4, 3, -5

Question 9.
If cos α, cos β, cos γ are the direction cosines of a line then the value of sin² α + sin²β + sin²γ is
(A) 1
(B) 2
(C) 3
(D) 4
Solution:
(B) 2

Question 10.

(A) null vector
(B) the unit vector along the line
(C) any vector along the line
(D) a vector perpendicular to the line
Solution:
(B) the unit vector along the line

Question 11.

(A) [0, 6]
(B) [-3, 6]
(C) [3, 6]
(D) [1, 2]
Solution:
(A) [0, 6]

Question 12.

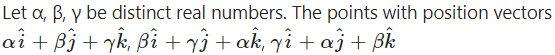
(A) are collinear
(B) form an equilateral triangle
(C) form a scalene triangle
(D) form a right angled triangle
Solution:
(B) form an equilateral triangle

Question 13.

(A) 9p² = 4q²
(B) 4p² = 9q²
(C) 9p = 4q
(D) 4p = 9q
Solution:
(A) 9p² = 4q²

Question 14.

Question 15.

(A) 30º
(B) 45º
(C) 60º
(D) 90º
Solution:
(A) 30º

Question 16.

Question 17.

(A) 0
(B) -1
(C) 1
(D) 3
Solution:
(C) 1

Question 18.
(A) The arithmetic mean of a and b
(B) The geometric mean of a and b
(C) The harmonic man of a and b
(D) 0
Solution:
(B) The geometric mean of a and b

Question 19.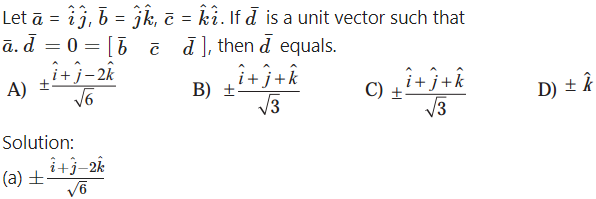

Question 20.

II Answer the following :
1) ABCD is a trapezium with AB parallel to DC and DC = 3AB. M is the mid-point of DC,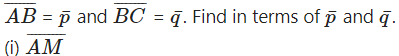

Solution:

Solution:

Solution:

Solution: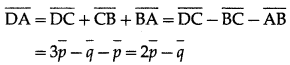

Question 2.

Question 3.
In a pentagon ABCDE

Solution:

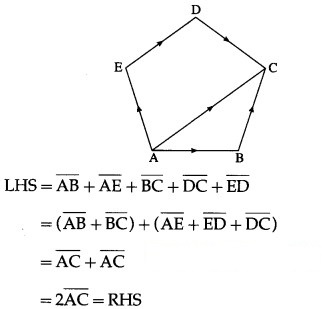
Question 4.

Solution:
ABCD is a parallelogram

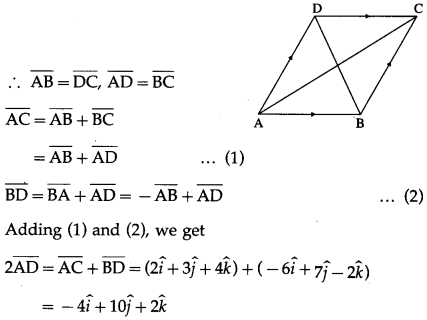
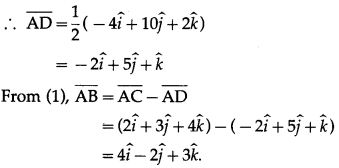
Question 5.

Solution:


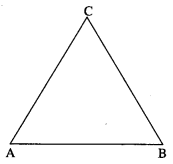
By triangle law of vectors

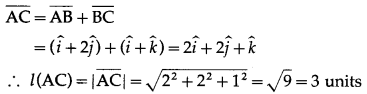
Hence, the length of third side is 3 units.

Question 6.

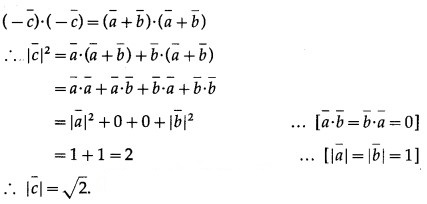
Question 7.
Find the lengths of the sides of the triangle and also determine the type of a triangle.
(i) A(2, -1, 0), B(4, 1, 1,), C(4, -5, 4)
Solution:
The position vectors a¯, b¯, c¯ of the points A, B, C are


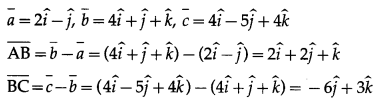
∴ ∆ ABC is right angled at A.

(ii) L(3, -2, -3), M(7, 0, 1), N (1, 2, 1)
Solution:


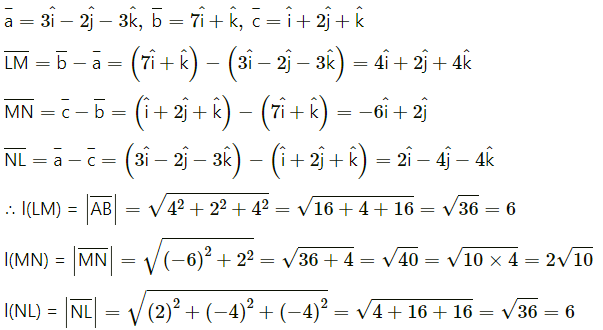
l(LM) = 6, l(MN) = 2√10 , l(NL) = 6
∆LMN is sosceles

Question 8.
Find the component form of if a if

Solution:

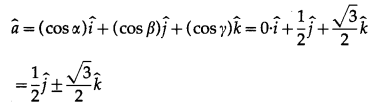
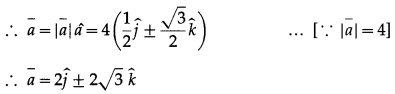
Solution:

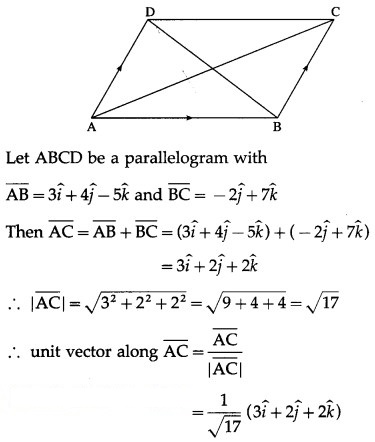
Question 10.
If D, E, F are the mid-points of the sides BC, CA, AB of a triangle ABC , prove

Solution:

Since D, E, F are the midpoints of BC, CA, AB respec-tively, by the midpoint formula

Question 11.
Find the unit vectors that are parallel to the tangent line to the parabola y = x² at the point (2, 4)
Solution:
Differentiating y = x² w.r.t. x, we get  = 2x

∴ the equation of tangent at P is
y – 4 = 4(-2)
∴ y = 4x – 4
∴ y = 4x is equation of line parallel to the tangent at P and passing through the origin O.

∴ the direction ratios of this line are 1, 4, 0
∴ its direction cosines are

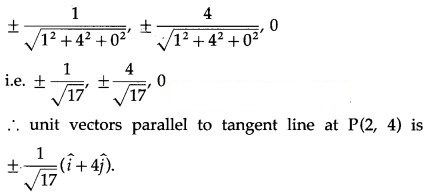
Question 12.

Solution:

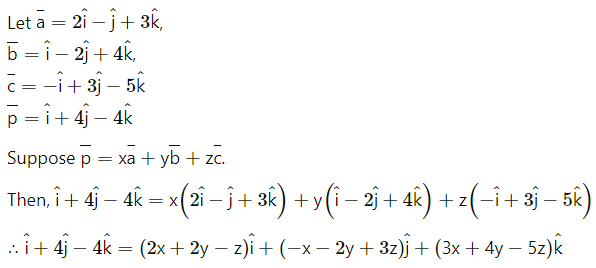
By equality of vectors,
2x + 2y – z = 1
-x – 2y + 3z = 4
3x + 4y – 5z = -4
We have to solve these equations by using Cramer’s Rule.

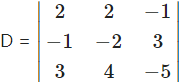
= 2(10 – 12) – 2(5 – 9) – 1(-4 + 6)
= -4 + 8 – 2
= 2 ≠ 0

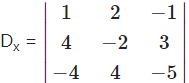
= 1(10 – 12) – 2(-20 + 12) – 1 (16 – 8)
= -2 + 16 – 8
= 6

= 2(-20 + 12) – 1(5 – 9) – 1(4 – 12)
= -16 – 4 – 8
= -28

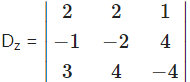
= 2(8 – 16) – 2(4 – 12) + 1(-4 + 6)
= -16 – 16 + 2
= -30

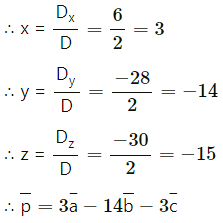
Question 13.

Solution:

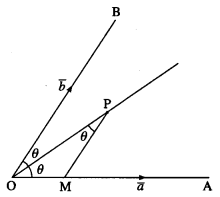
Choose any point P on the angle bisector of ∠AOB. Draw PM parallel to OB.
∴ ∠OPM = ∠POM
= ∠POB
Hence, OM = MP

Question 14.
The position vectors f three consecutive vertices of a parallelogram



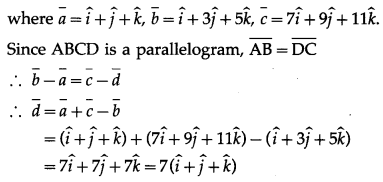
∴ coordinates of B are (-4, 9, 6).

Question 16.
Prove that the sum of the three vectors determined by the medians of a triangle directed from the vertices is zero.
Solution:


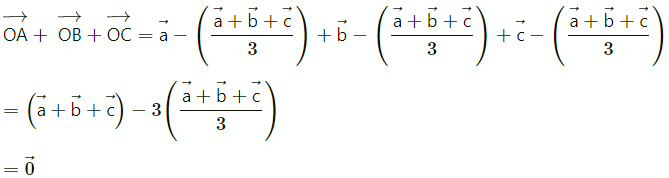
Hence, Sum os the three vectors determined by the medians of a triangle directed from the vertices is zero.

Question 17.
ABCD is a parallelogram E, F are the mid points of BC and CD respectively. AE, AF meet the diagonal BD at Q and P respectively. Show that P and Q trisect DB.
Solution:


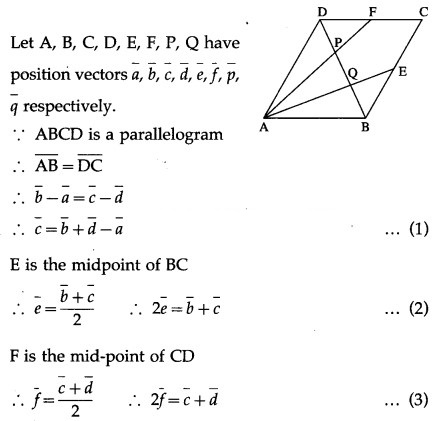
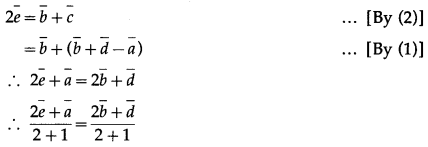
LHS is the position vector of the point on AE and RHS is the position vector of the point on DB. But AE and DB meet at Q.

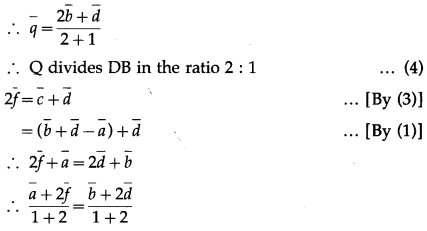
LHS is the position vector of the point on AF and RHS is the position vector of the point on DB.
But AF and DB meet at P.

∴ P divides DB in the ratio 1 : 2 … (5)
From (4) and (5), if follows that P and Q trisect DB.

Question 18.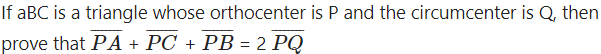

Solution:
Let G be the centroid of the ∆ ABC.

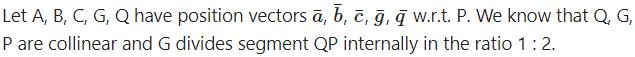
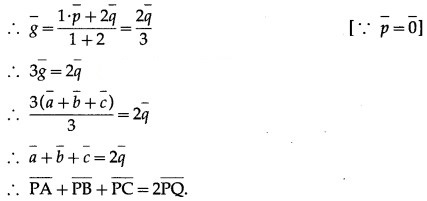
Question 19.

We know that Q, G, P are collinear and G divides segment QP internally in the ratio 1 : 2
∴ by section formula for internal division,

Question 20.
In a triangle OAB, E is the midpoint of BO and D is a point on AB such that AD: DB = 2:1. If OD and AE intersect at P, determine the ratio OP:PD using vector methods.
Solution:

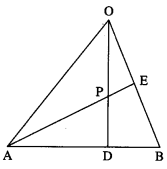
∵ AD : DB = 2 : 1.
∴ D divides AB internally in the ratio 2 : 1.
Using section formula for internal division, we get

LHS is the position vector of the point which divides OD internally in the ratio 3 : 2.
RHS is the position vector of the point which divides AE internally in the ratio 4 : 1.
But OD and AE intersect at P
∴ P divides OD internally in the ratio 3 : 2.
Hence, OP : PD = 3 : 2.

Question 21.

Solution:

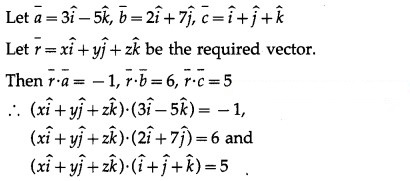
∴ 3x – 5z= -1 … (1)
∴ 2x + 7y = 6 … (2)
∴ x + y + z = 5 … (3)
From (3), z = 5 – x – y
Substituting this value of z in (1), we get
∴ 3x – 5(5 – x – y)= -1
∴ 8x + 5y = 24 … (4)
Multiplying (2) by 4 and subtracting from (4), we get
8x + 5y – 4(2x + 7y) = 24 – 6 × 4
∴ -23y = 0 ∴ y = 0
Substituting y = 0 in (2), we get
∴ 2x = 6 ∴ x = 3
Substituting x = 3 in (1), we get
∴ 3(3) – 5z = -1
∴ 5z = -10 ∴ z = 2

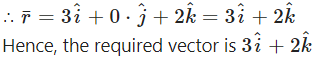
Question 22.


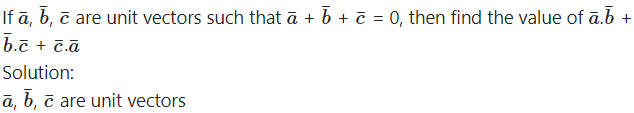
Adding (2), (3), (4) and using the fact that scalar product commutative, we get

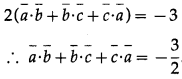
Question 23.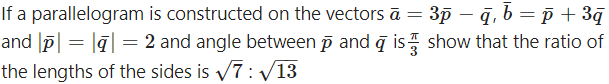

Solution:




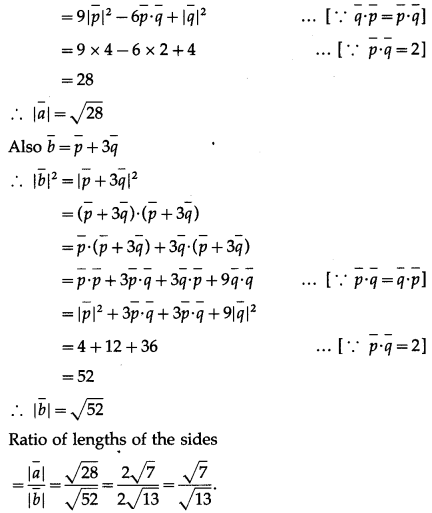
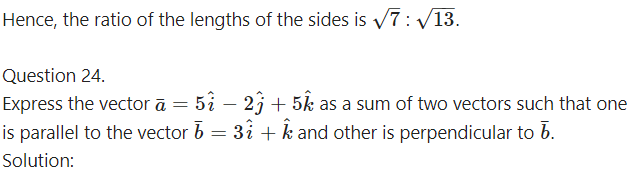
By equality of vectors
3m + x = 5 … (1)
y = -2
and m – 3x = 5
From (1) and (2)
3m + x = m – 3x
∴ 2m = -4x m ∴ m = -2x
Substituting m = -2x in (1), we get
∴ -6x + x = 5 ∴ -5x = 5 ∴ x = -1
∴ m = -2x = 2

Question 25.

Solution:

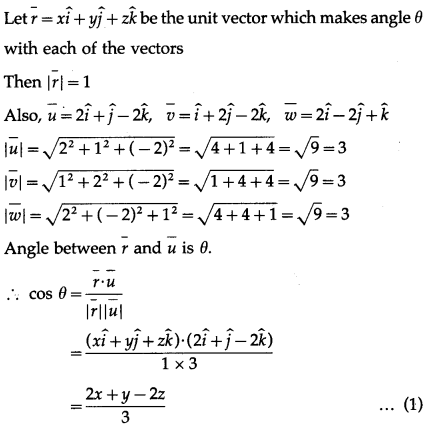
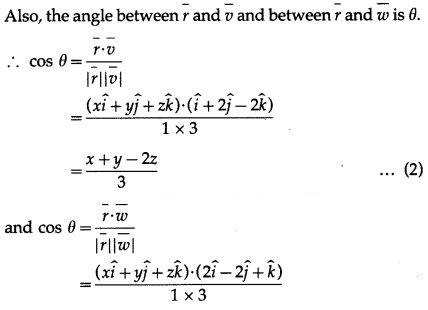
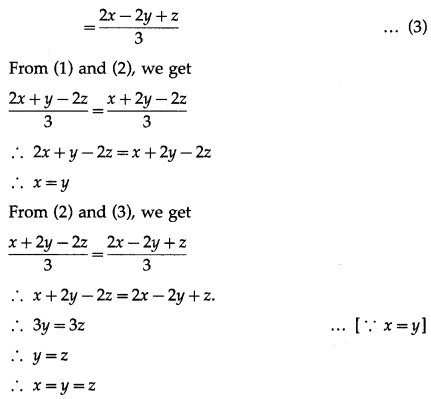
Question 26.
Find the acute angles between the curves at their points of intersection. y = x², y = x³
Solution:
The angle between the curves is same as the angle between their tangents at the points of intersection. We find the points of intersection of y = x² … (1)
and y = x³ … (2)
From (1) and (2)
x³ = x²
∴ x³ – x² = 0
∴ x²(x – 1) = 0
∴ x = 0 or x = 1
When x = 0, y = 0.
When x = 1, y = 1.

∴ equation of tangent to y = x³ at P is y = 0.
∴ the tangents to both curves at (0, 0) are y = 0
∴ angle between them is 0.
Angle at P = (1, 1)
Slope of tangent to y = x² at P

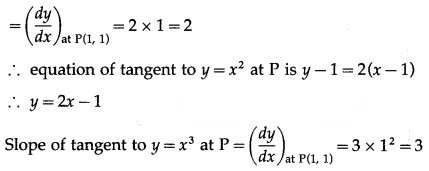
∴ equation of tangent to y = x³ at P is y – 1 = 3(x – 1) y = 3x – 2
We have to find angle between y = 2x – 1 and y = 3x – 2
Lines through origin parallel to these tagents are y = 2x and y = 3x

These lines lie in XY-plane.
∴ the direction ratios of these lines are 1, 2, 0 and 1, 3, 0.
The angle θ between them is given by

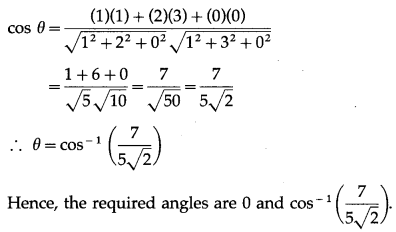
Question 27.
Find the direction cosines and direction angles of the vector.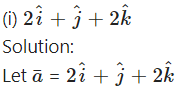

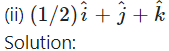
Question 28.

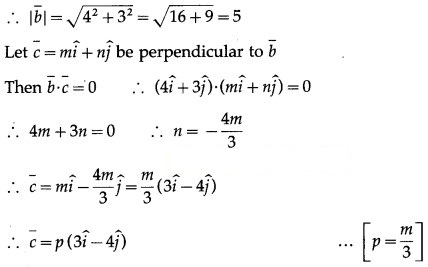
Question 29.
Show that no line in space can make angle π/6 and π/4 with X- axis and Y-axis.
Solution:
Let, if possible, a line in space make angles π/6 and π/4 with X-axis and Y-axis.


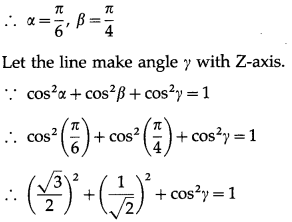
This is not possible, because cos γ is real
∴ cos²γ cannot be negative.
Hence, there is no line in space which makes angles π/6 and π/4 with X-axis and Y-axis.

Question 30.
Find the angle between the lines whose direction cosines are given by the equation 6mn – 2nl + 5lm = 0, 3l + m + 5n = 0
Solution:
Given 6mn – 2nl + 5lm = o
3l + m +5n = 0.
From (2), m = 3l – 5n
Putting the value of m in equation (1), we get,
⇒ 6n(-3l – 5n) – 2nl + 5l(-3l – 5n) = 0
⇒ -18nl- 30n – 2nl- 15l2 – 25nl = 0
⇒ – 30n² – 45nl – 15l² = 0
⇒ 2n² + 3nl + l² = 0
⇒ 2n² + 2nl + nl + l² = 0
⇒ (2n + l) (n + l) = 0
∴ 2n + l = 0 OR n + l = 0
∴ l = -2n OR l = -n
∴ l = -2n
From (2), 3l + m + 5n = 0
∴ -6n + m + 5n = 0
∴ m = n
i.e. (-2n, n, n) = (-2, 1, 1)
∴ l = -n
∴ -3n + m + 5n = 0
∴ m = -2n
i.e. (-n, -2n, n) = (1, 2, -1)
(a₁, b₁, c₁) = (-2, 1, 1) and (a₂, b₃, c₃) = (1, 2, -1)

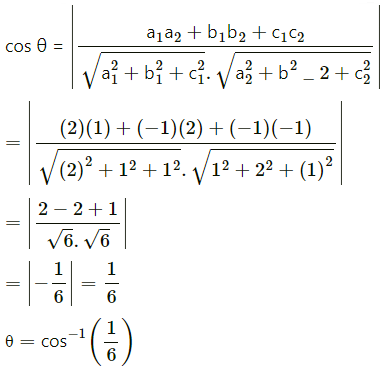
Question 31.
If Q is the foot of the perpendicular from P(2, 4, 3) on the line joining the points A(1, 2, 4) and B(3, 4, 5), find coordinates of Q.
Solution:
Let PQ be the perpendicular drawn from point P(2, 4, 3) to the line joining the points A(1, 2, 4) and B (3, 4, 5).
Let Q divides AB internally in the ratio λ : 1

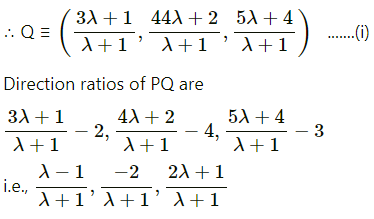
Now, direction ratios of AB are, 3 – 1, 4 – 2, 5 – 4 i.e., 2, 2, 1.

Coordinates of Q are,

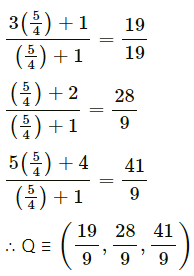
Question 32.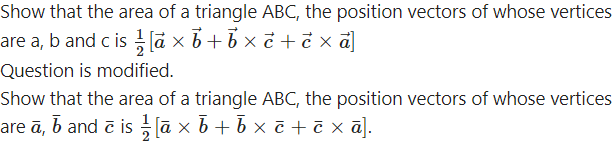

Solution:

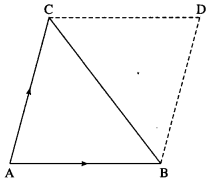
Consider the triangle ABC.
Complete the parallelogram ABDC.
Vector area of ∆ABC

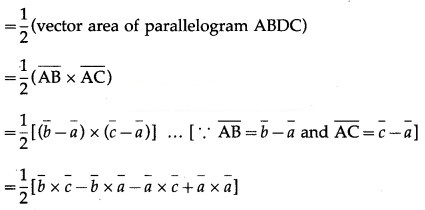
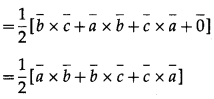
Question 33.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0), and (0, 0, c). What is the area of the triangle with these vertices?
Solution:

Question 34.
State whether each expression is meaningful. If not, explain why ? If so, state whether it is a vector or a scalar.

Solution:
This is the scalar product of two vectors. Therefore, this expression is meaningful and it is a scalar.

Solution:

Solution:
This is vector product of two vectors. Therefore, this expression is meaningful and it is a vector.

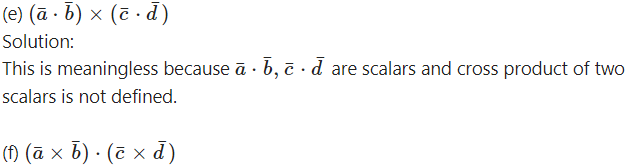
Solution:
This is scalar product of two vectors. Therefore, this expression is meaningful and it is a scalar.

Solution:
This is a scalar multiplication of a vector. Therefore, this expression is meaningful and it is a vector.

Solution:
This is the product of two scalars. Therefore, this expression is meaningful and it is a scalar.

Solution:
This is the scalar product of two vectors. Therefore, this expression is meaningful and it is a scalar.

Solution:
This is the sum of scalar and vector which is not defined. Therefore, this expression is meaningless.

Question 35.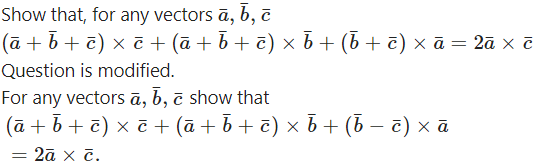

Solution:

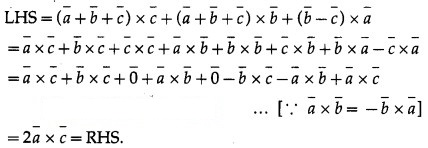
Question 36.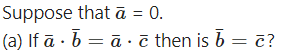

Solution:

Solution:

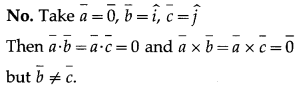
Question 37.
If A(3, 2, -1), B(-2, 2, -3), C(3, 5, -2), D(-2, 5, -4) then
(i) verify that the points are the vertices of a parallelogram and
Solution:

∴ opposite sides AB and DC of ABCD are parallel and equal.
∴ ABCD is a parallelogram.

(ii) find its area.
Solution:

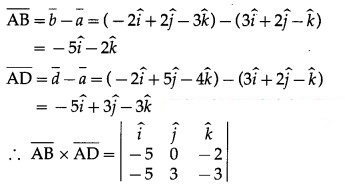
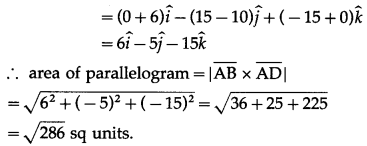
Question 38.

Question 39.

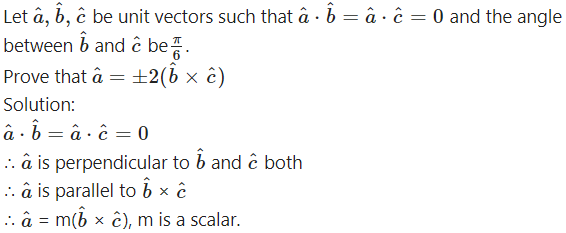
Question 40.

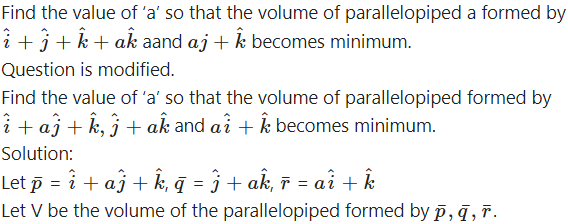
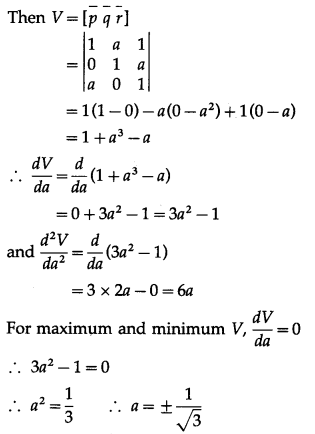
Question 41.
Find the volume of the parallelepiped spanned by the diagonals of the three faces of a cube of side a that meet at one vertex of the cube.
Solution:

Take origin O as one vertex of the cube and OA, OB and OC as the positive directions of the X-axis, the Y-axis and the Z-axis respectively.
Here, the sides of the cube are
OA = OB = OC = a
∴ the coordinates of all the vertices of the cube will be
O = (0, 0, 0) A = (a, 0, 0)
B = (0, a, 0) C = (0, 0, a)
N = (a, a, 0) L = (0, a, a)
M = (a, 0, a) P = (a, a, a)
ON, OL, OM are the three diagonals which meet at the vertex O

Question 42.

Solution:

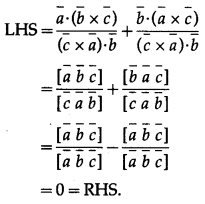
Question 43.

Solution:

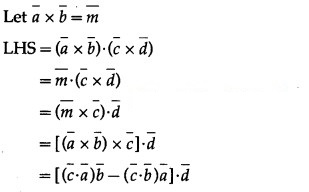
Question 44.

Question 45.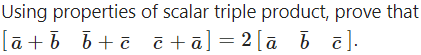
Solution:

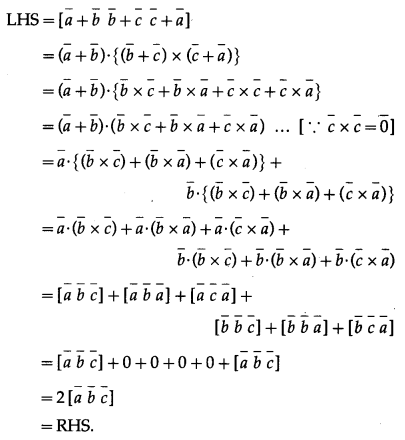
Question 46.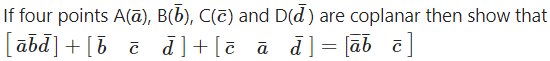

Solution:

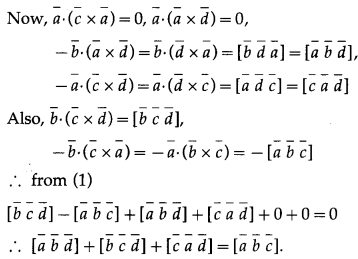
Question 47.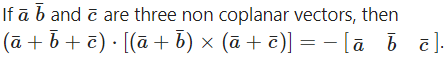

Solution:

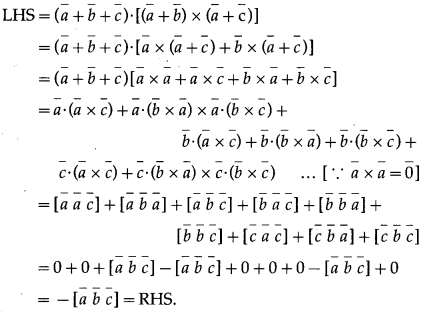
Question 48.
If in a tetrahedron, edges in each of the two pairs of opposite edges are perpendicular, then show that the edges in the third pair are also perpendicular.
Solution:

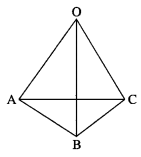
Let O-ABC be a tetrahedron. Then o
(OA, BC), (OB, CA) and (OC, AB) are the pair of opposite edges.

 
∴ the third pair (OC, AB) is perpendicular.