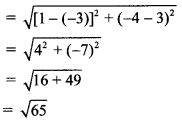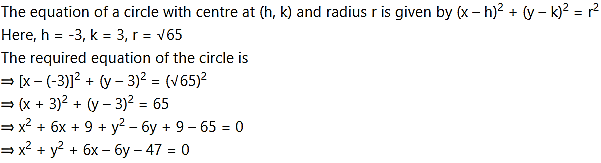Chapter 6 Circle Ex 6.1
Chapter 6 Circle Ex 6.1
Question 1.
Find the equation of a circle with
(i) centre at origin and radius 4.
(ii) centre at (-3, -2) and radius 6.
(iii) centre at (2, -3) and radius 5.
(iv) centre at (-3, -3) passing through point (-3, -6).
Solution:
(i) The equation of a circle with centre at origin and radius ‘r’ is given by
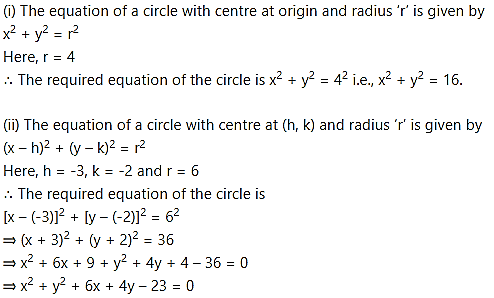
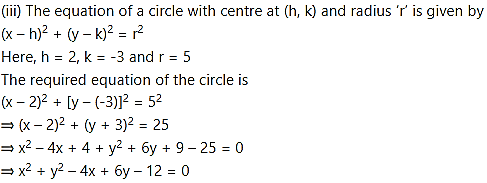
(iv) Centre of the circle is C (-3, -3) and it passes through the point P (-3, -6).
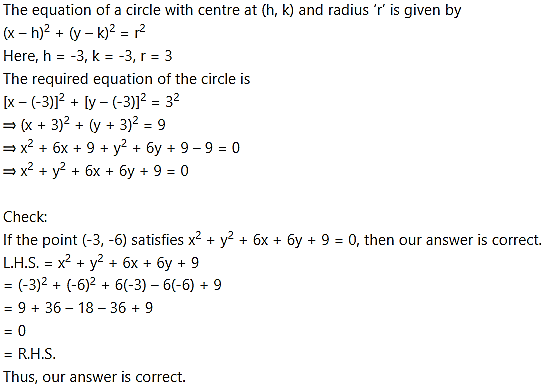
Question 2.
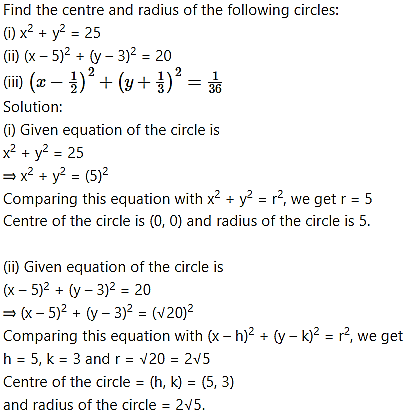
(iii) Given the equation of the circle is
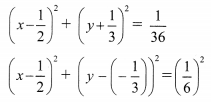
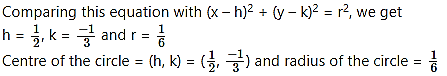
Question 3.
Find the equation of the circle with centre
(i) at (a, b) and touching the Y-axis.
(ii) at (-2, 3) and touching the X-axis.
(iii) on the X-axis and passing through the origin having radius 4.
(iv) at (3, 1) and touching the line 8x – 15y + 25 = 0.
Solution:
(i) Since the circle is touching the Y-axis, the radius of the circle is X-co-ordinate of the centre.
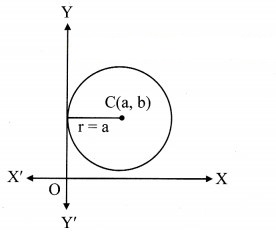
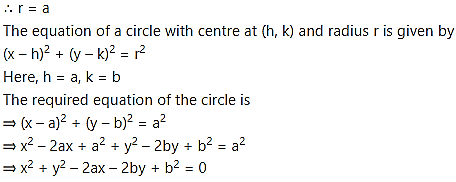
(ii) Since the circle is touching the X-axis, the radius of the circle is the Y co-ordinate of the centre.
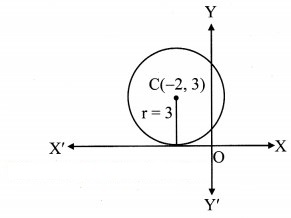
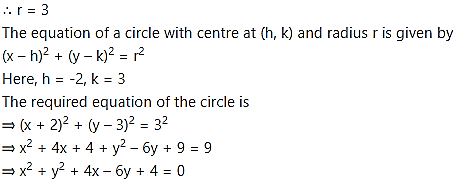
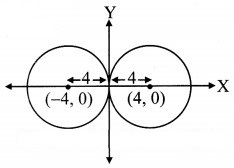
(iii) Let the co-ordinates of the centre of the required circle be C (h, 0).
Since the circle passes through the origin i.e., O(0, 0)
OC = radius
⇒ = 16
⇒ h = ±4
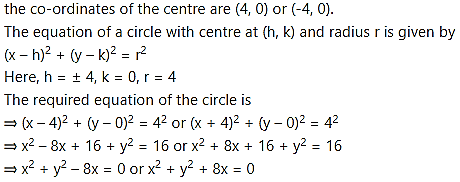
(iv) Centre of the circle is C (3, 1).
Let the circle touch the line 8x – 15y + 25 = 0 at point M.
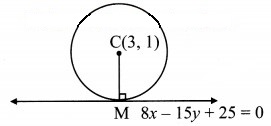
CM = radius (r)
CM = Length of perpendicular from centre C(3, 1) on the line 8x – 15y + 25 = 0
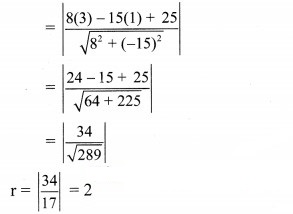
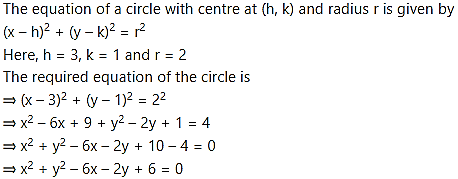
Question 4.
Find the equation of the circle, if the equations of two diameters are 2x + y = 6 and 3x + 2y = 4 and radius is 9.
Solution:
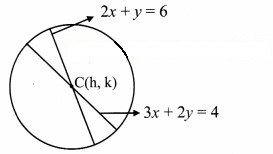
Given equations of diameters are 2x + y = 6 and 3x + 2y = 4.
Let C (h, k) be the centre of the required circle.
Since point of intersection of diameters is the centre of the circle,
x = h, y = k
Equations of diameters become
2h + k = 6 …..(i)
and 3h + 2k = 4 ……..(ii)
By (ii) – 2 × (i), we get
-h = -8
⇒ h = 8
Substituting h = 8 in (i), we get
2(8) + k = 6
⇒ k = 6 – 16
⇒ k = -10
Centre of the circle is C (8, -10) and radius, r = 9
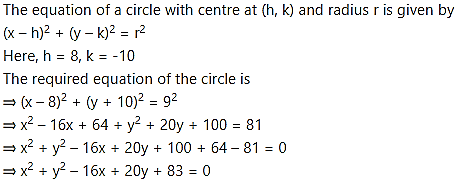
Question 5.
If y = 2x is a chord of the circle – 10x = 0, find the equation of the circle with this chord as diameter.
Solution:
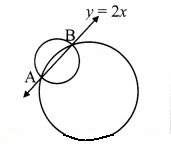
Question 6.
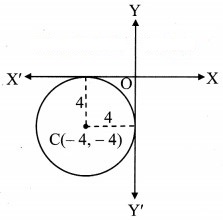
Find the equation of a circle with a radius of 4 units and touch both the co-ordinate axes having centre in the third quadrant.
Solution:
The radius of the circle = 4 units
Since the circle touches both the co-ordinate axes and its centre is in the third quadrant,
the centre of the circle is C(-4, -4).
Question 7.
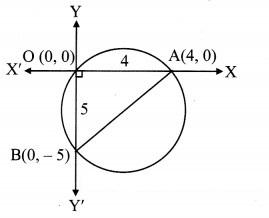
Find the equation of the circle passing through the origin and having intercepts 4 and -5 on the co-ordinate axes.
Solution:
Let the circle intersect X-axis at point A and intersect Y-axis at point B.
the co-ordinates of point A are (4, 0) and the co-ordinates of point B are (0, -5).
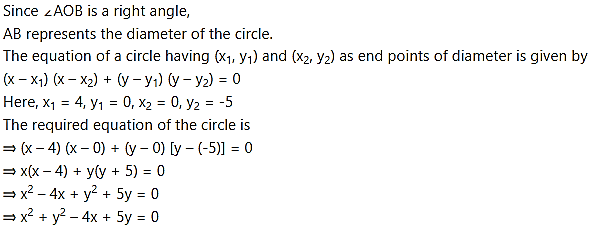
Question 8.
Find the equation of a circle passing through the points (1, -4), (5, 2) and having its centre on line x – 2y + 9 = 0.
Solution:
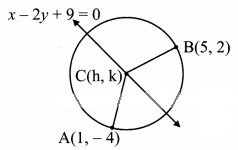
Let C(h, k) be the centre of the required circle which lies on the line x – 2y + 9 = 0.
Equation of line becomes
h – 2k + 9 = 0 …..(i)
Also, the required circle passes through points A(1, -4) and B(5, 2).
CA = CB = radius
CA = CB
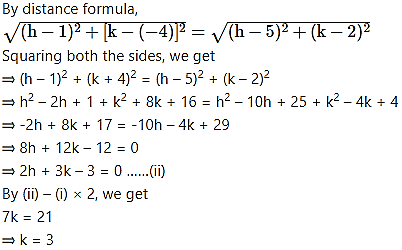
Substituting k = 3 in (i), we get
h – 2(3) + 9 = 0
⇒ h – 6 + 9 = 0
⇒ h = -3
Centre of the circle is C(-3, 3).
radius (r) = CA
