Chapter 6 Circle Practice Set 6.3
Chapter 6 Circle Practice Set 6.3
Question 1.
Construct ∆ABC such that ∠B =100°, BC = 6.4 cm, ∠C = 50° and construct its incircle.
Solution:

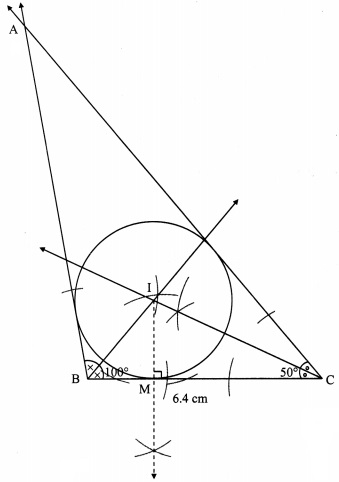
Steps of construction:
i. Construct ∆ABC of the given measurement.
ii. Draw the bisectors of ∠B and ∠C. Let these bisectors intersect at point I.
iii. Draw a perpendicular IM on side BC. Point M is the foot of the perpendicular.
iv. With I as centre and IM as radius, draw a circle which touches all the three sides of the triangle.
Question 2.
Construct ∆PQR such that ∠P = 70°, ∠R = 50°, QR = 7.3 cm and construct its circumcircle.
Solution:
In ∆PQR,
m∠P + m∠Q + m∠R = 180° … [Sum of the measures of the angles of a triangle is 180°]
∴ 70° + m∠Q + 50° = 180°
∴ m∠Q = 180° – 70° + m∠Q + 50° = 180°
∴ m∠Q = 180° – 70° – 50°
∴ m∠Q = 60°


Steps of construction:
i. Construct A PQR of the given measurement.
ii. Draw the perpendicular bisectors of side PQ and side QR of the triangle.
iii. Name the point of intersection of the perpendicular bisectors as point C.
iv. Join seg CP
v. With C as centre and CP as radius, draw a circle which passes through the three vertices of the triangle.
Question 3.
Construct ∆XYZ such that XY = 6.7 cm, YZ = 5.8 cm, XZ = 6.9 cm. Construct its incircle.
Solution:
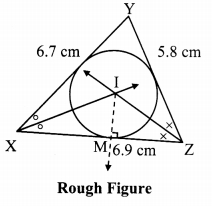
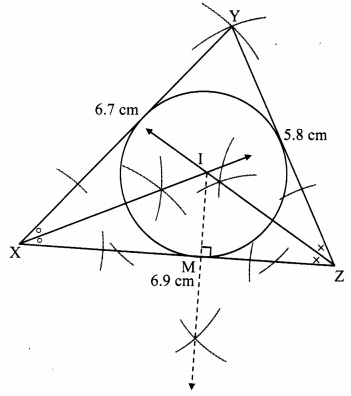
Steps of construction:
i. Construct ∆XYZ of the given measurement
ii. Draw the bisectors of ∠X and ∠Z. Let these bisectors intersect at point I.
iii. Draw a perpendicular IM on side XZ. Point M is the foot of the perpendicular.
iv. With I as centre and IM as radius, draw a circle which touches all the three sides of the triangle.
Question 4.
In ∆LMN, LM = 7.2 cm, ∠M = 105°, MN = 6.4 cm, then draw ∆LMN and construct its circumcircle.
Solution:

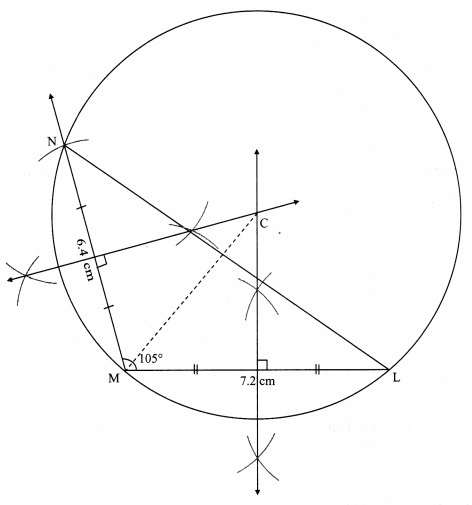
Steps of construction:
i. Construct ∆LMN of the given measurement.
ii. Draw the perpendicular bisectors of side MN and side ML of the triangle.
iii. Name the point of intersection of the perpendicular bisectors as point C.
iv. Join seg CM
v. With C as centre and CM as radius, draw a circle which passes through the three vertices of the triangle.
Question 5.
Construct ∆DEF such that DE = EF = 6 cm. ∠F = 45° and construct its circumcircle.
Solution:
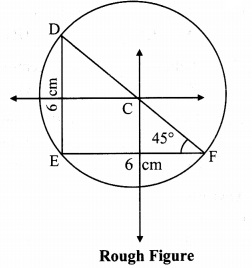

Steps of construction:
i. Construct ∆DEF of the given measurement.
ii. Draw the perpendicular bisectors of side DE and side EF of the triangle.
iii. Name the point of intersection of perpendicular bisectors as point C.
iv. Join seg CE
v. With C as centre and CE as radius, draw a circle which passes through the three vertices of the triangle.
Intext Questions and Activities
Question 1.
Draw any equilateral triangle. Draw incircle and circumcircle of it. What did you observe while doing this activity? (Textbook pg. no. 85)
i. While drawing incircle and circumcircle, do the angle bisectors and perpendicular bisectors coincide with each other?
ii. Do the incentre and circumcenter coincide with each other? If so, what can be the reason of it?
iii. Measure the radii of incircle and circumcircle and write their ratio.
Solution:
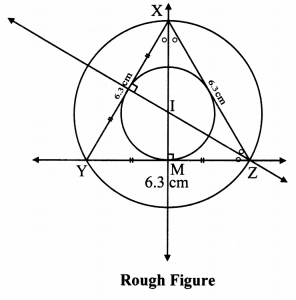
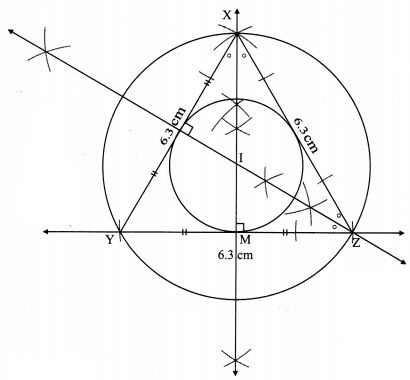
Steps of construction:
i. Construct equilateral ∆XYZ of any measurement.
ii. Draw the perpendicular bisectors of side XY and side YZ of the triangle.
iii. Draw the bisectors of ∠X and ∠Z.
iv. Name the point of intersection of the perpendicular bisectors and angle bisectors as point I.
v. With I as centre and IM as radïus, draw a circle which touches all the three sides of the triangle.
vi. With I as centre and IZ as radius, draw a circle which passes through the three vertices of the triangle.
[Note: Here, point of intersection of perpendicular bisector and angle bisector is same.]
i. Yes.
ii. Yes.
The angle bisectors of the angles and the perpendicular bisectors of the sides of an equilateral triangle are coincedent. Hence, its incentre and circumcentre coincide.
iii. Radius of circumcircle = 3.6 cm,
Radius of incircle = 1.8 cm
![]()