Chapter 6 Differential Equations Ex 6.3

Chapter 6 Differential Equations Ex 6.3

Question 1.
In each of the following examples verify that the given expression is a solution of the corresponding differential equation.

Solution:
xy = log y + c
Differentiating w.r.t. x, we get

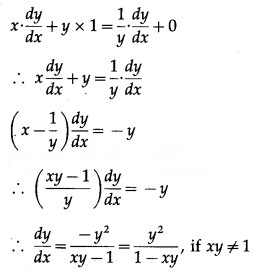
Hence, xy = log y + c is a solution of the D.E.

Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

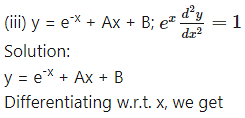
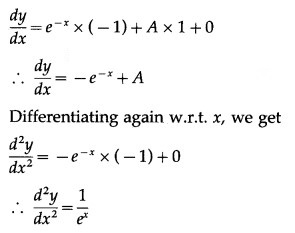
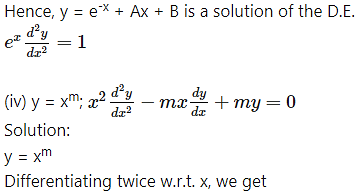
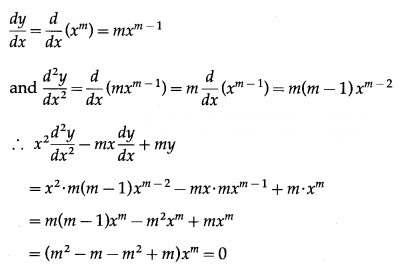
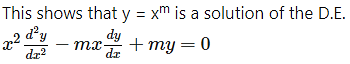
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

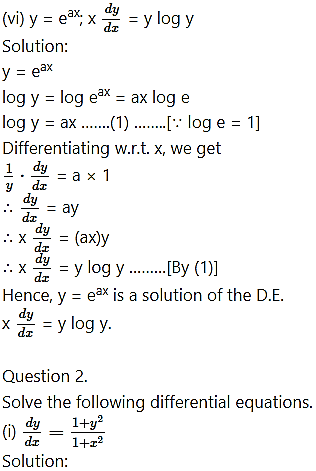
Solution:

This is the general solution.

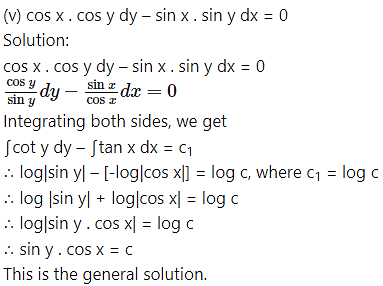
Multiplying throughout by 4, this becomes

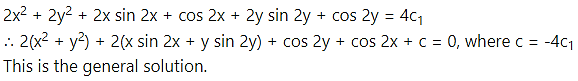
Solution:

Solution:

This is the general solution.

Question 3.
For each of the following differential equations, find the particular solution satisfying the given condition:

When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5

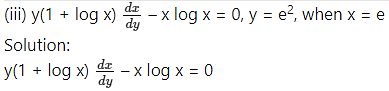
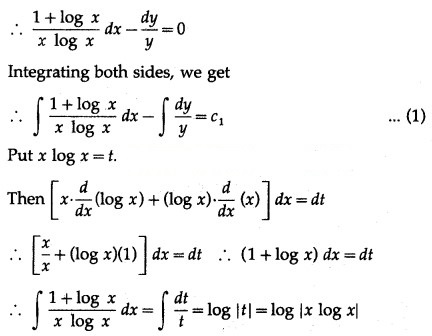
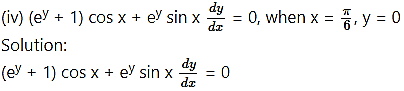
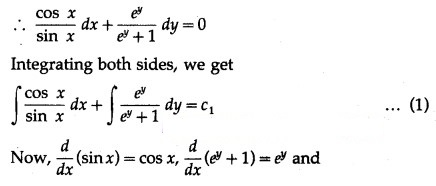
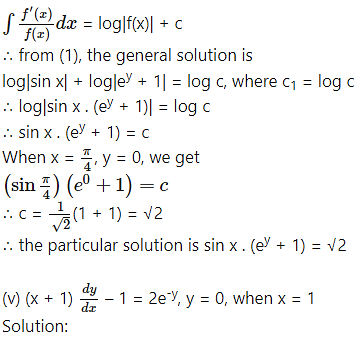
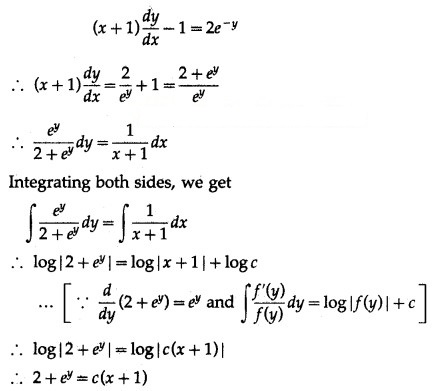
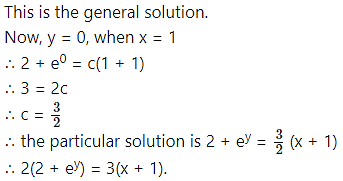
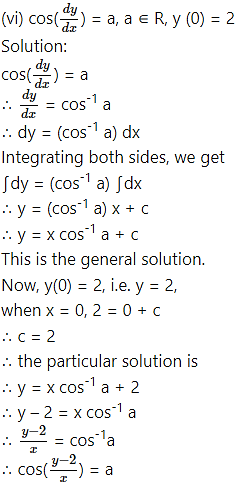
Question 4.
Reduce each of the following differential equations to the variable separable form and hence solve:

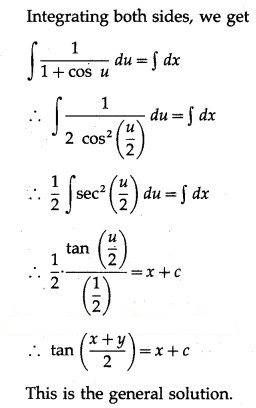
Solution:

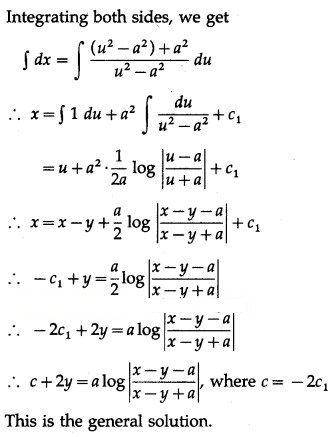
Solution:

Integrating both sides, we get

Integrating both sides, we get
∫dx = ∫seu du
∴ x = tan u + c
∴ x = tan(x – 2y) + c
This is the general solution.

(v) (2x – 2y + 3) dx – (x – y + 1) dy = 0, when x = 0, y = 1
Solution:
(2x – 2y + 3) dx – (x – y + 1) dy = 0
∴ (x – y + 1) dy = (2x – 2y + 3) dx

∴ u – log|u + 2| = -x + c
∴ x – y – log|x – y + 2| = -x + c
∴ (2x – y) – log|x – y + 2| = c
This is the general solution.
Now, y = 1, when x = 0.
∴ (0 – 1) – log|0 – 1 + 2| = c
∴ -1 – o = c
∴ c = -1
∴ the particular solution is
(2x – y) – log|x – y + 2| = -1
∴ (2x – y) – log|x – y + 2| + 1 = 0