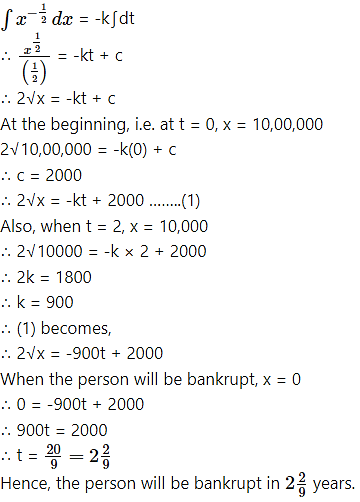Chapter 6 Differential Equations Miscellaneous Exercise 6
Chapter 6 Differential Equations Miscellaneous Exercise 6
(I) Choose the correct option from the given alternatives:
Question 1.
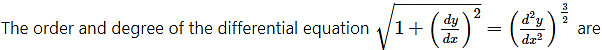
respectively……..
(a) 2, 1
(b) 1, 2
(c) 3, 2
(d) 2, 3
Answer:
(d) 2, 3
Question 2.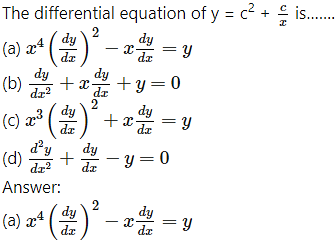
Question 3.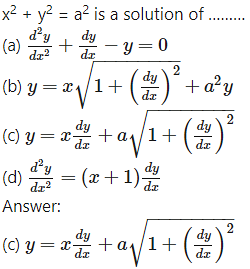
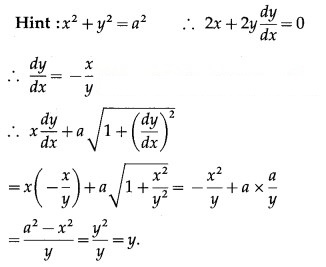
Question 4.
The differential equation of all circles having their centres on the line y = 5 and touching the X-axis is
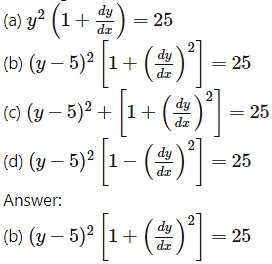
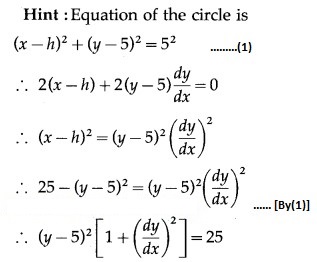
Question 5.
(a) circles
(b) parabolas
(c) ellipses
(d) hyperbolas
Answer:
(a) circles
Hint:
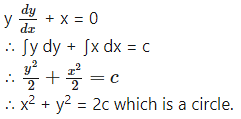
Question 6.
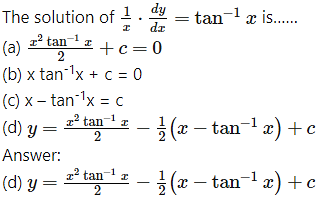
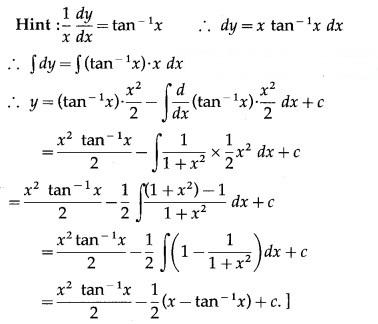
Question 7.
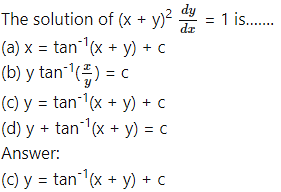
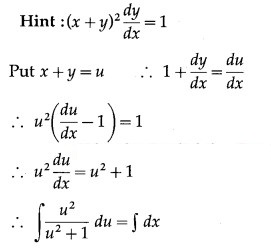
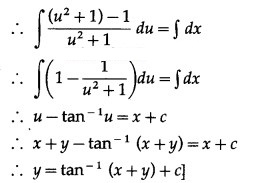
Question 8.
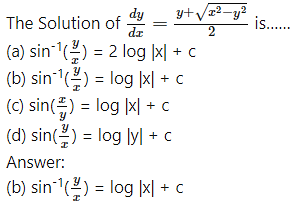
Question 9.
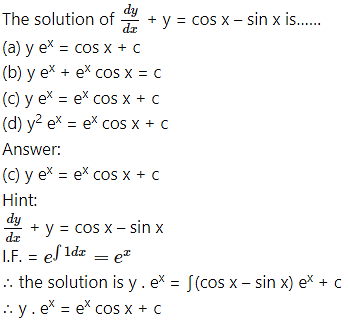
Question 10.
Question 11.
The solution of the differential equation dy/dx= sec x – y tan x is…….
(a) y sec x + tan x = c
(b) y sec x = tan x + c
(c) sec x + y tan x = c
(d) sec x = y tan x + c
Answer:
(b) y sec x = tan x + c
Hint:
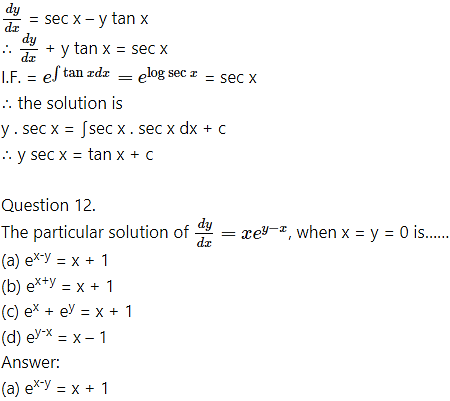
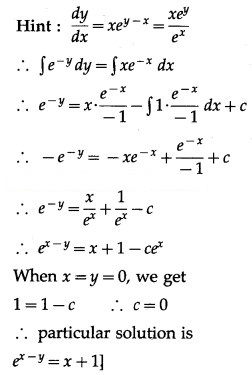
Question 13.
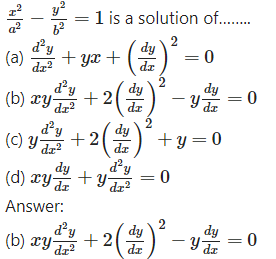
Question 14.
The decay rate of certain substances is directly proportional to the amount present at that instant. Initially, there are 27 grams of substance and 3 hours later it is found that 8 grams left. The amount left after one more hour is……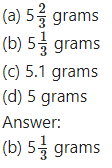
Question 15.
If the surrounding air is kept at 20°C and the body cools from 80°C to 70°C in 5 minutes, the temperature of the body after 15 minutes will be…..
(a) 51.7°C
(b) 54.7°C
(c) 52.7°C
(d) 50.7°C
Answer:
(b) 54.7°C
(II) Solve the following:
Question 1.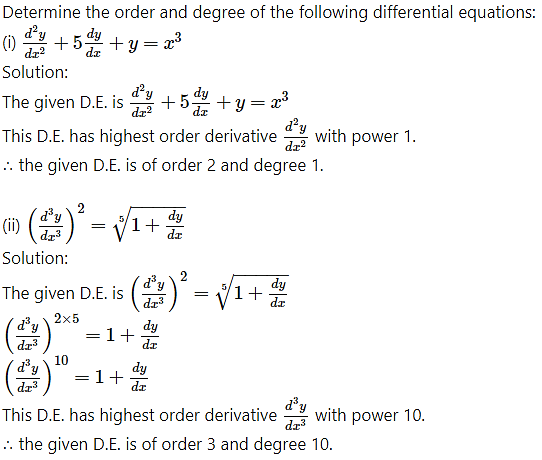
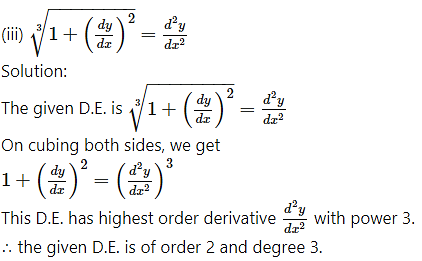
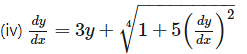
Solution:
The given D.E. is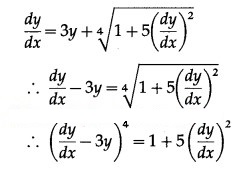
Differentiating both sides w.r.t. x, we get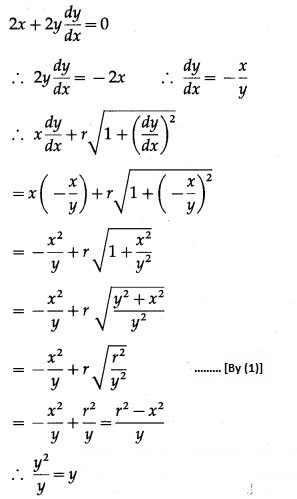
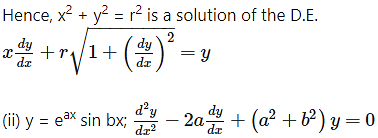
Solution:
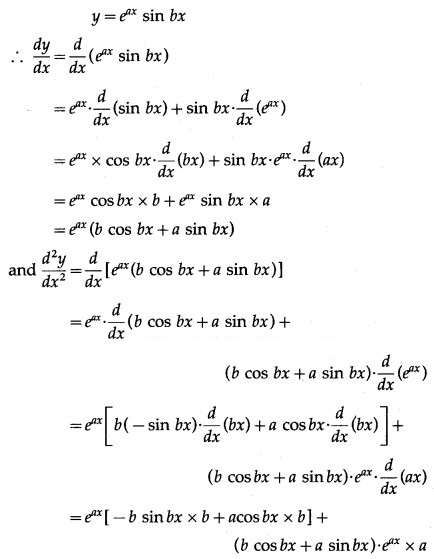
Solution:
y = 3 cos(log x) + 4 sin (log x) …… (1)
Differentiating both sides w.r.t. x, we get
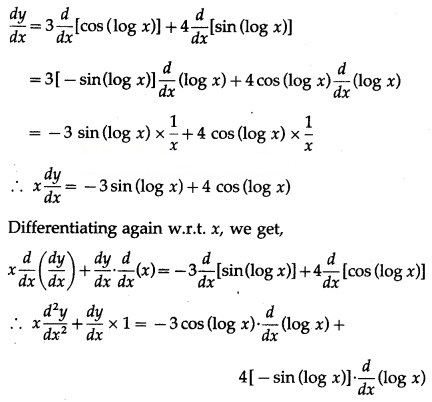
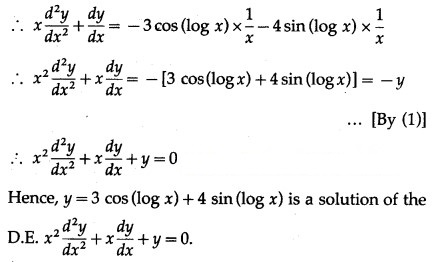
Solution:
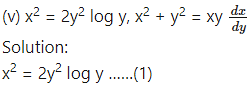
Differentiating both sides w.r.t. y, we get
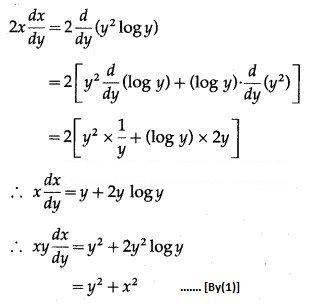
Question 3.
Obtain the differential equation by eliminating the arbitrary constants from the following equations:
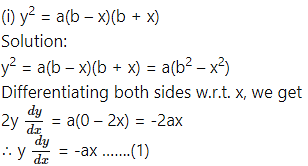
Differentiating again w.r.t. x, we get
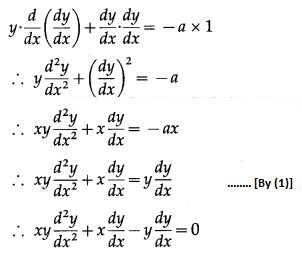
This is the required D.E.
(ii) y = a sin(x + b)
Solution:
y = a sin(x + b)
This is the required D.E.
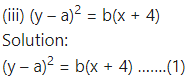
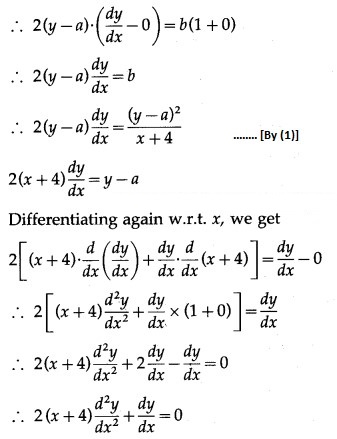
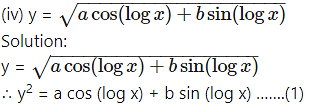
Differentiating both sides w.r.t. x, we get
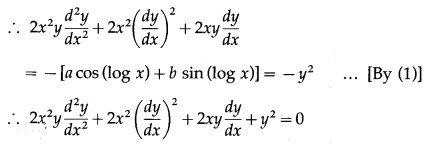
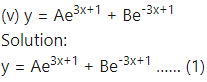
Differentiating twice w.r.t. x, we get
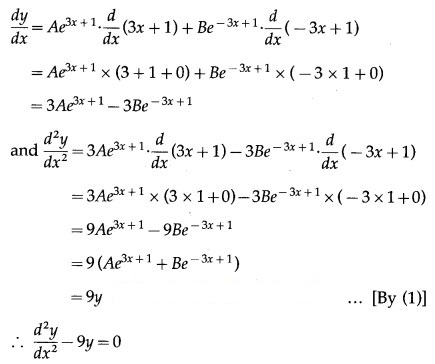
This is the required D.E.
Question 4.
Form the differential equation of:
(i) all circles which pass through the origin and whose centres lie on X-axis.
Solution:
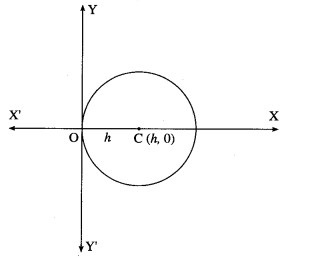
Let C (h, 0) be the centre of the circle which pass through the origin. Then radius of the circle is h.
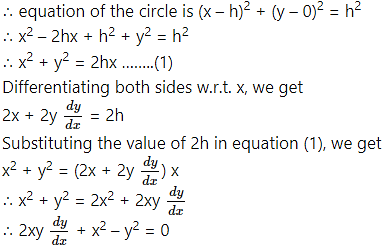
This is the required D.E.
(ii) all parabolas which have 4b as latus rectum and whose axis is parallel to Y-axis.
Solution:
Let A(h, k) be the vertex of the parabola which has 4b as latus rectum and whose axis is parallel to the Y-axis.
Then equation of the parabola is
(x – h = 4b(y – k) ……. (1)
where h and k are arbitrary constants.
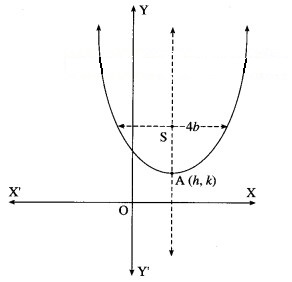
Differentiating both sides of (1) w.r.t. x, we get
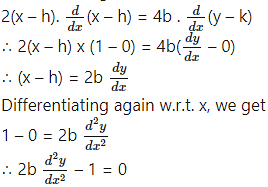
This is the required D.E.
(iii) an ellipse whose major axis is twice its minor axis.
Solution:
Let 2a and 2b be lengths of the major axis and minor axis of the ellipse.
Then 2a = 2(2b)
∴ a = 2b
∴ equation of the ellipse is
This is the required D.E.
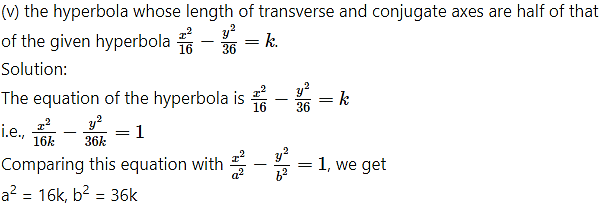
∴ a = 4√k, b = 6√k
∴ l(transverse axis) = 2a = 8√k
and l(conjugate axis) = 2b = 12√k
Let 2A and 2B be the lengths of the transverse and conjugate axes of the required hyperbola.
Then according to the given condition
2A = a = 4√k and 2B = b = 6√k
∴ A = 2√k and B = 3√k
∴ equation of the required hyperbola is
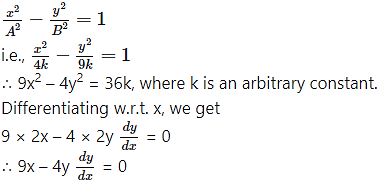
This is the required D.E.
Question 5.
Solve the following differential equations:
Solution:
Solution: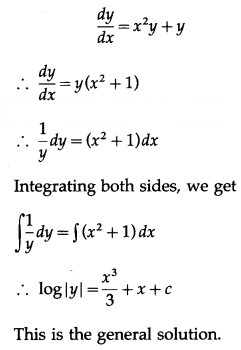
Solution:
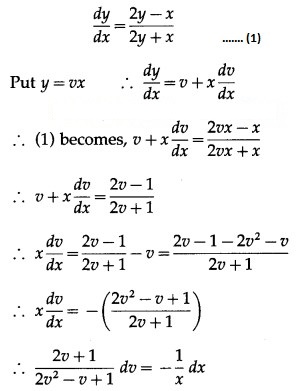
(iv) x dy = (x + y + 1) dx
Solution:
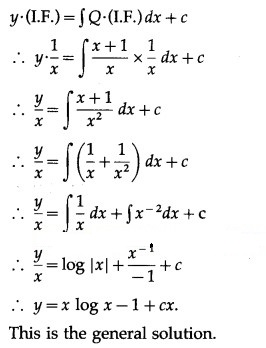
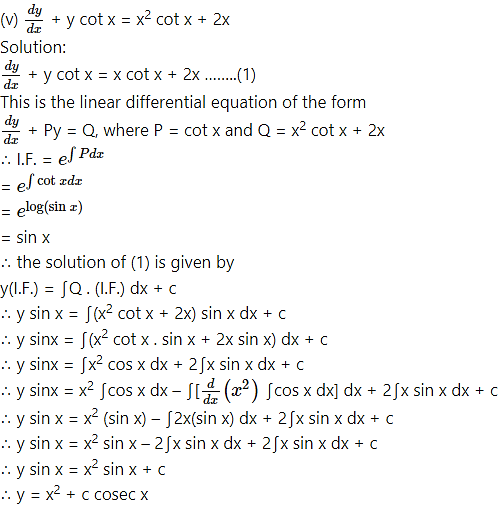
This is the general solution.
Solution:
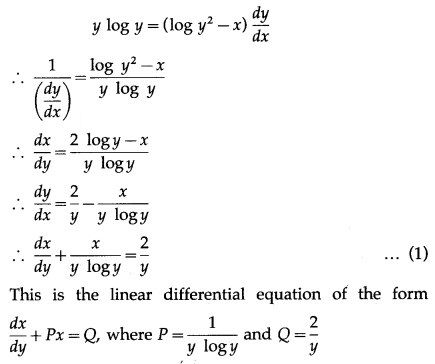
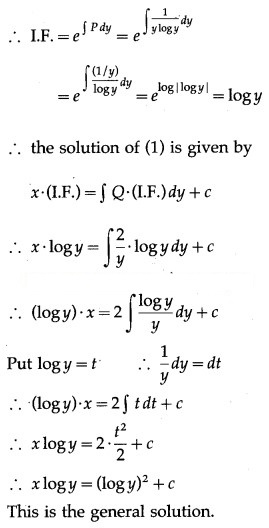
Solution:
Question 6.
Find the particular solution of the following differential equations:
Solution:
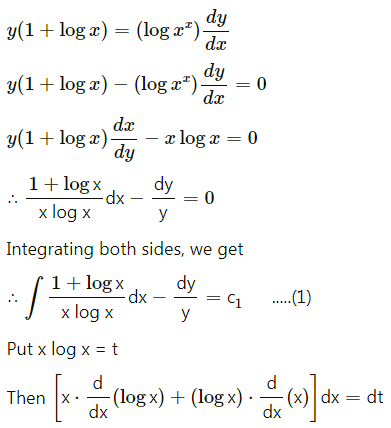
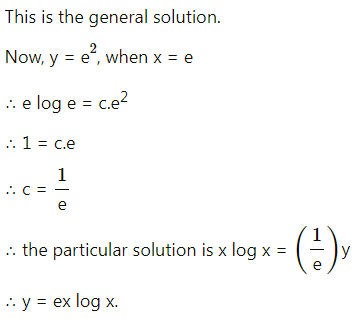
Solution:
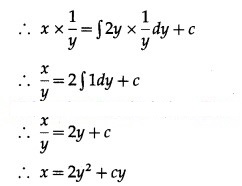
This is the general solution.
When x = 2, y = 1, we have
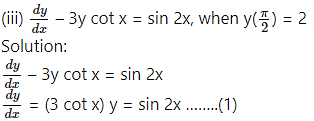
This is the linear differential equation of the form
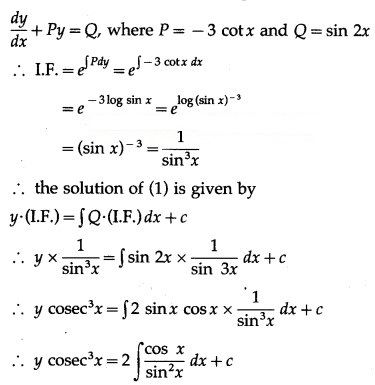
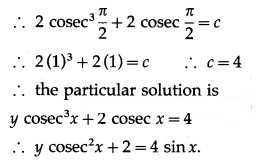
(iv) (x + y) dy + (x – y) dx = 0; when x = 1 = y
Solution:
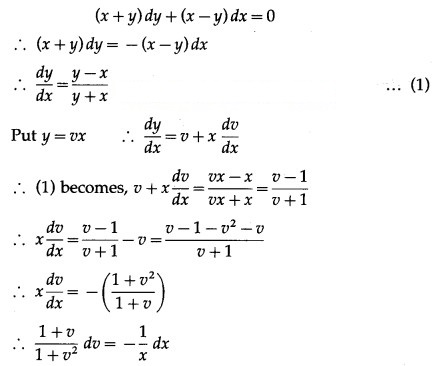
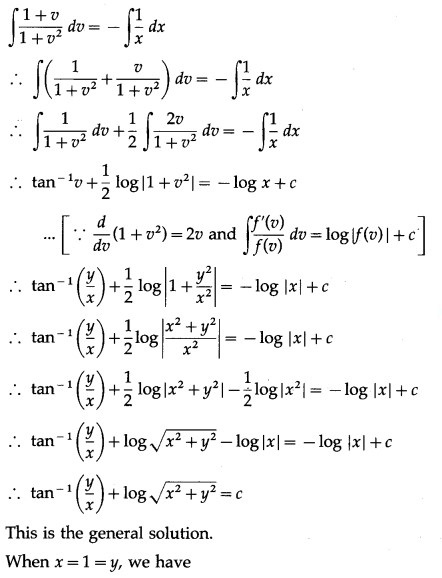
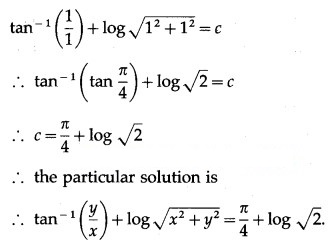
Solution:
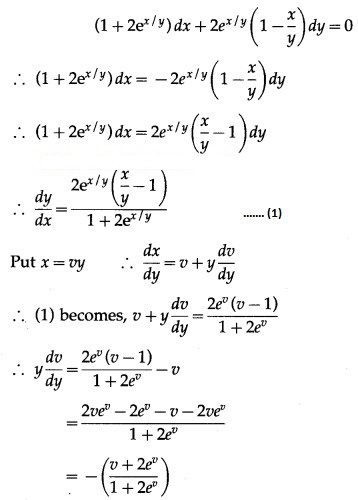
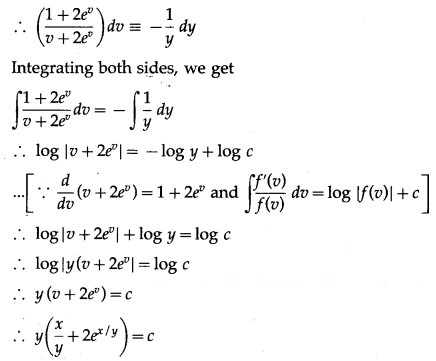
Question 7.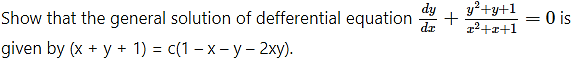
Solution:
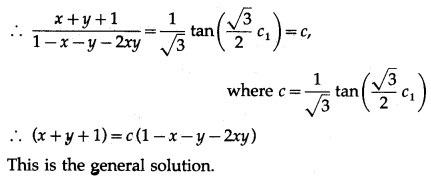
Question 8.
The normal lines to a given curve at each point (x, y) on the curve pass through (2, 0). The curve passes through (2, 3). Find the equation of the curve.
Solution:
Let P(x, y) be a point on the curve y = f(x).
∴ equation of the normal is
This is the general equation of the curve.
Since, the required curve passed through the point (2, 3), we get
Question 9.
The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after t seconds.
Solution:
Let r be the radius and V be the volume of the spherical balloon at any time t.
Then the rate of change in volume of the spherical balloon is which is a constant.
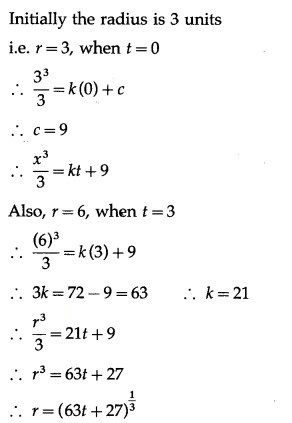
Hence, the radius of the spherical balloon after t seconds is (63t+27 units.
Question 10.
A person’s assets start reducing in such a way that the rate of reduction of assets is proportional to the square root of the assets existing at that moment. If the assets at the beginning are ₹ 10 lakhs and they dwindle down to ₹ 10,000 after 2 years, show that the person will be bankrupt in 
years from the start.
Solution:
Integrating both sides, we get
