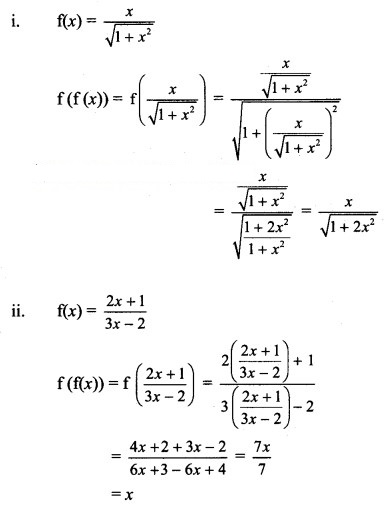Chapter 6 Functions Miscellaneous Exercise 6
Chapter 6 Functions Miscellaneous Exercise 6
(I) Select the correct answer from the given alternatives.
Question 1.
If log (5x – 9) – log (x + 3) = log 2, then x = ________
(A) 3
(B) 5
(C) 2
(D) 7
Answer:
(B) 5
Hint:
Question 3.
Find x, if 2 log2 x = 4
(A) 4, -4
(B) 4
(C) -4
(D) not defined
Answer:
(B) 4
Hint:
∴ x = ±4
∴ x = 4
Question 4.
Question 5.
(A) x – 1
(B) 1 – x
(C) x
(D) -x
Answer:
(C) x
Hint:
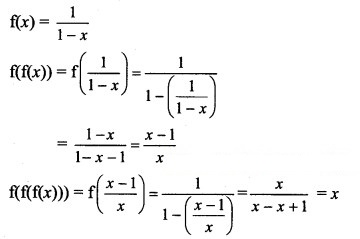
Question 6.
If f: R → R is defined by f(x) = x3, then f-1 (8) is equal to:
(A) {2}
(B) {-2.2}
(C) {-2}
(D) (-2.2)
Answer:
(A) {2}
Hint:
Question 7.
Question 8.
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
(A) -2
(B) 0
(C) 1
(D) 2
Answer:
(B) 0
Hint:
Question 9.
(A) R
(B) Z
(C) R – Z
(D) Q – {0}
Answer:
(C) R – Z
Hint:
For f to be defined, {x} ≠ 0
∴ x cannot be integer.
∴ Domain = R – Z
Question 10.
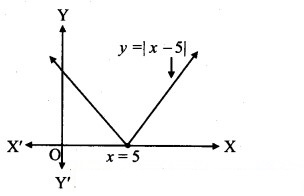
The domain and range of f(x) = 2 – |x – 5| are
(A) R+, (-∞, 1]
(B) R, (-∞, 2]
(C) R, (-∞, 2)
(D) R+, (-∞, 2]
Answer:
(B) R, (-∞, 2]
Hint:
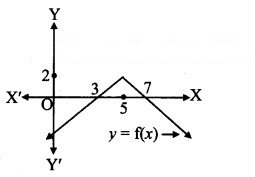
f(x) = 2 – |x – 5|
= 2 – (5 – x), x < 5
= 2 – (x – 5), x ≥ 5
∴ f(x) = x – 3, x < 5
= 7 – x, x ≥ 5
Domain = R,
Range (from graph) = (-∞, 2]
(II) Answer the following:
Question 1.
Which of the following relations are functions? If it is a function determine its domain and range.
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}
(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2) (9, 3), (9, -3), (16, 4), (16, -4)}
(iii) {(2, 1), (3, 1), (5, 2)}
Solution:
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}
Every element of set A has been assigned a unique element in set B
∴ Given relation is a function
Domain = {2, 4, 6, 8, 10, 12, 14}, Range = {1, 2, 3, 4, 5, 6, 7}
(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2) (9, 3), (9, -3) (16, 4), (16, -4)}
∵ (1, 1), (1, -1) ∈ the relation
∴ Given relation is not a function.
As element 1 of the domain has not been assigned a unique element of co-domain.
(iii) {(2, 1), (3, 1), (5, 2)}
Every element of set A has been assigned a unique element in set B.
∴ Given relation is a function.
Domain = {2, 3, 5}, Range = {1, 2}
Question 2.
Question 3.
Find whether the following functions are onto or not.
(i) f: Z → Z defined by f(x) = 6x – 7 for all x ∈ Z
(ii) f: R → R defined by f(x) = x2 + 3 for all x ∈ R
Solution:
(i) f(x) = 6x – 7 = y (say)
(x, y ∈ Z)
∴ x = 7+y/6
Since every integer y does not give integer x, f is not onto.
(ii) f(x) = x2 + 3 = y (say)
(x, y ∈ R)
Clearly y ≥ 3 …..[ x2 ≥ 0]
∴ All the real numbers less than 3 from codomain R, have not been pre-assigned any element from the domain R.
∴ f is not onto.
Question 4.
Let f: R → R be a function defined by f(x) = 5 x3 – 8 for all x ∈ R. Show that f is one-one and onto. Hence find f-1.
Solution:
Question 5.
A function f: R → R defined by f(x) = 3x/5+ 2, x ∈ R. Show that f is one-one and onto. Hence find f-1.
Solution:
Question 6.
A function f is defined as f(x) = 4x + 5, for -4 ≤ x < 0. Find the values of f(-1), f(-2), f(0), if they exist.
Solution:
f(x) = 4x + 5, -4 ≤ x < 0
f(-1) = 4(-1) + 5 = -4 + 5 = 1
f(-2) = 4(-2) + 5 = -8 + 5 = -3
x = 0 ∉ domain of f
∴ f(0) does not exist.
Question 7.
A function f is defined as f(x) = 5 – x for 0 ≤ x ≤ 4. Find the values of x such that
(i) f(x) = 3
(ii) f(x) = 5
Solution:
(i) f(x) = 3
∴ 5 – x = 3
∴ x = 5 – 3 = 2
(ii) f(x) = 5
∴ 5 – x = 5
∴ x = 0
Question 8.
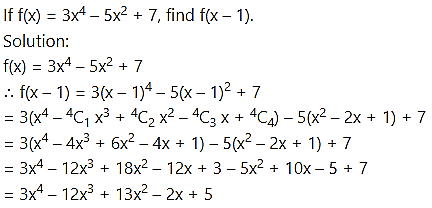
Question 9.
If f(x) = 3x + a and f(1) = 7, find a and f(4).
Solution:
f(x) = 3x + a, f(1) = 7
∴ 3(1) + a = 7
∴ a = 7 – 3 = 4
∴ f(x) = 3x + 4
∴ f(4) = 3(4) + 4 = 12 + 4 = 16
Question 10.
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Solution:
f(x) = ax2 + bx + 2
f(1) = 3
∴ a(1)2 + b(1) + 2 = 3
∴ a + b = 1 ….(i)
f(4) = 42
∴ a(4)2 + b(4) + 2 = 42
∴ 16a + 4b = 40
Dividing by 4, we get
4a + b = 10 …..(ii)
Solving (i) and (ii), we get
a = 3, b = -2
Question 11.
Find composite of f and g:
(i) f = {(1, 3), (2, 4), (3, 5), (4, 6)}
g = {(3, 6), (4, 8), (5, 10), (6, 12)}
(ii) f = {(1, 1), (2, 4), (3, 4), (4, 3)}
g = {(1, 1), (3, 27), (4, 64)}
Solution:
(i) f = {(1, 3), (2, 4), (3, 5), (4, 6)}
g = {(3, 6), (4, 8), (5, 10), (6, 12)}
∴ f(1) = 3, g(3) = 6
f(2) = 4, g(4) = 8
f(3) = 5, g(5)=10
f(4) = 6, g(6) = 12
(gof) (x) = g (f(x))
(gof)(1) = g(f(1)) = g(3) = 6
(gof)(2) – g(f(2)) = g(4) = 8
(gof)(3) = g(f(3)) = g(5) = 10
(gof)(4) = g(f(4)) = g(6) = 12
∴ gof = {(1, 6), (2, 8), (3, 10), (4, 12)}
(ii) f = {(1, 1), (2, 4), (3, 4), (4, 3)}
g = {(1, 1), (3, 27), (4, 64)}
f(1) = 1, g(1) = 1
f(2) = 4, g(3) = 27
f(3) = 4, g(4) = 64
f(4) = 3
(gof) (x) = g(f(x))
(gof) (1) = g(f(1)) = g(1) = 1
(gof) (2) = g(f(2)) = g(4) = 64
(gof) (3) = g(f(3)) = g(4) = 64
(gof) (4) = g(f(4)) = g(3) = 27
∴ gof = {(1, 1), (2, 64), (3, 64), (4, 27)}
Question 12.
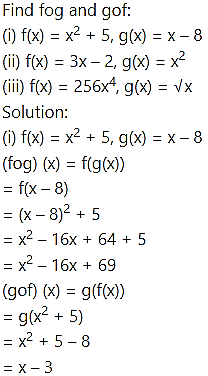
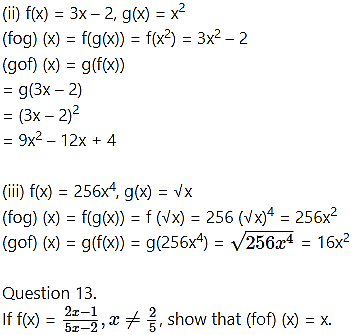
Solution:
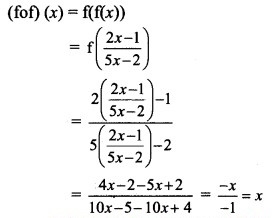
Question 14.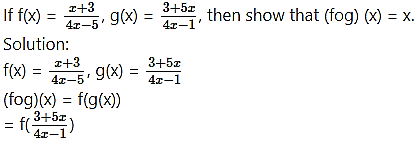
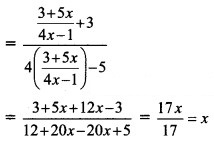
Question 15.
Solution:
f(x) = , x ≠ 2
∴ f(x) = x + 2, x ≠ 2 and g(x) = x + 2,
The domain of f = R – {2}
The domain of g = R
Here, f and g have different domains.
∴ f ≠ g
Question 16.
Let f: R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph.
Solution:
f(x) = x + 5
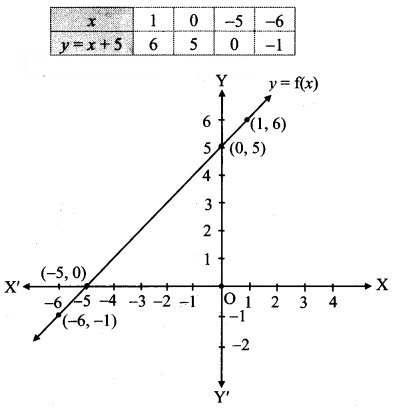
Question 17.
Let f: R → R be given by f(x) = x3 + 1 for all x ∈ R. Draw its graph.
Solution:
Let y = f(x) = x3 + 1
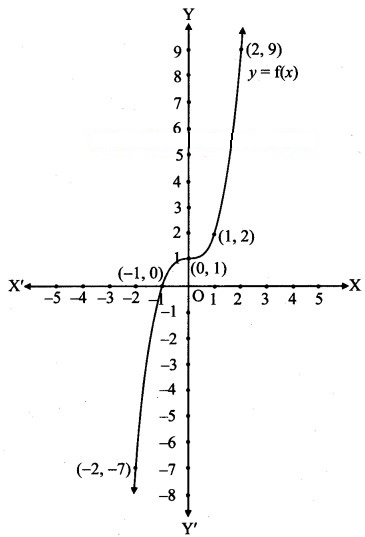
Question 18.
For any base show that log(1 + 2 + 3) = log 1 + log 2 + log 3
Solution:
L.H.S. = log(1 + 2 + 3) = log 6
R.H.S. = log 1 + log 2 + log 3
= 0 + log (2 × 3)
= log 6
∴ L.H.S. = R.H.S.
Question 19.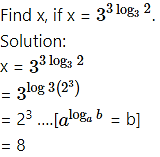
Question 20.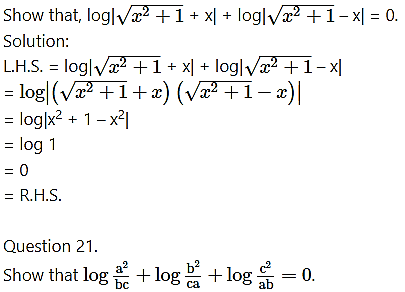
Solution:
Question 22.
Simplify log (log x4) – log(log x).
Solution:
log (log x4) – log (log x)
= log (4 log x) – log (log x) …..[log mn = n log m]
= log 4 + log (log x) – log (log x) …..[log (mn) = log m + log n]
= log 4
Question 23.
Solution:
Question 24.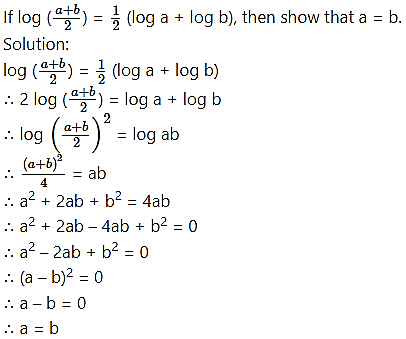
Question 25.
If b2 = ac. Prove that, log a + log c = 2 log b.
Solution:
b2 = ac
Taking log on both sides, we get
log b2 = log ac
∴ 2 log b = log a + log c
∴ log a + log c = 2 log b
Question 26.
Solve for x, logx (8x – 3) – logx 4 = 2.
Solution:
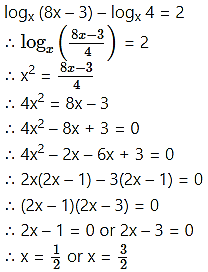
Question 27.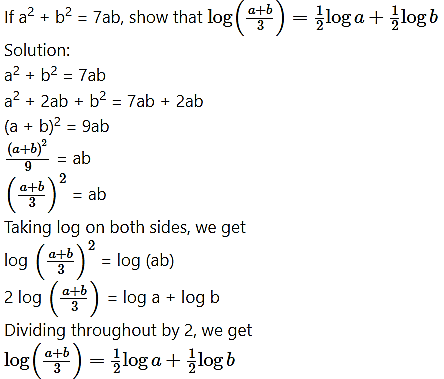
Question 28.
Solution: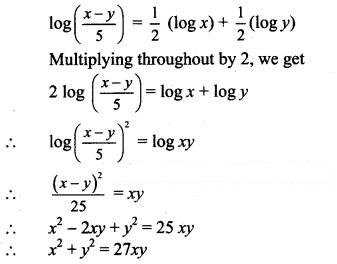
Question 29.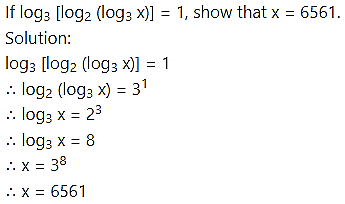
Question 30.
Solution:
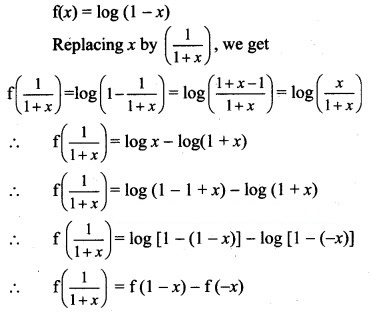
Question 31.
Solution:
Question 33.
Solution:
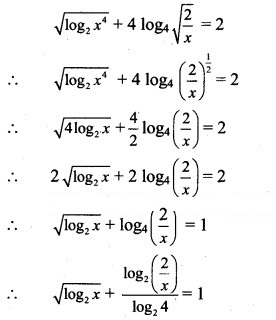
Question 34.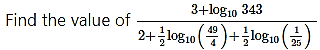
Solution:
Question 35.
∴ log a = k(x + y – 2z), log b = k(y + z – 2x), log c = k(z + x – 2y)
log a + log b + log c = k(x + y – 2z) + k(y + z – 2x) + k(z + x – 2y)
= k(x + y – 2z + y + z – 2x + z + x – 2y)
= k(0)
= 0
∴ log (abc) = log 1 …….[∵ log 1 = 0]
∴ abc = 1
Question 36.
Solution:
Question 37.
Solution:
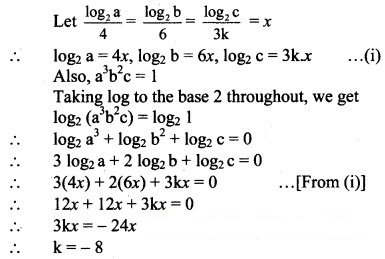
Question 38.
Solution:
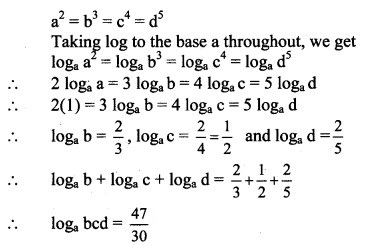
Question 39.
Solve the following for x, where |x| is modulus function, [x] is the greatest integer function, {x} is a fractional part function.
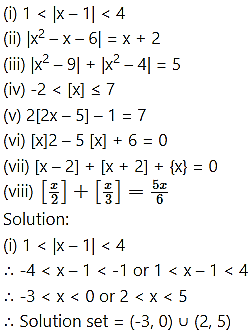
Case II: -3 ≤ x < -2
As x < -2, x < 3
∴ (x – 3) (x + 3) < 0, (x – 2) (x + 2) > 0
Equation (i) reduces to
-( x2 – 9) + x2 – 4 = 5
∴ 5 = 5 (true)
-3 ≤ x < -2 is a solution ….(ii)
Case III: -2 ≤ x < 2 As x > -3, x < 3
∴ (x – 3) (x + 3) < 0,
(x – 2) (x + 2) < 0
Equation (i) reduces to
9 – x2 + 4 – x2 = 5
∴ 2x2 = 13 – 5
∴ x2 = 4
∴ x = -2 is a solution …..(iii)
Case IV: 2 ≤ x < 3 As x > -3, x > -2
∴ (x – 3) (x + 3) < 0, (x – 2) (x + 2) > 0
Equation (i) reduces to
9 – x2 + x2 – 4 = 5
∴ 5 = 5 (true)
∴ 2 ≤ x < 3 is a solution ……(iv)
Case V: 3 ≤ x As x > -3, x > -2, x > 2
∴ (x + 3) (x – 3) > 0,
(x – 2) (x + 2) > 0
Equation (i) reduces to
x2 – 9 + x2 – 4 = 5
∴ 2 x2 = 18
∴ x2 = 9
∴ x = 3 …..(v)
(x = -3 rejected as x ≥ 3)
From (ii), (iii), (iv), (v), we get
∴ Solution set = [-3, -2] ∪ [2, 3]
(iv) -2 < [x] ≤ 7
∴ -2 < x < 8
∴ Solution set = (-2, 8)
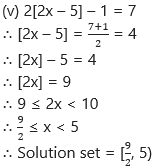
(vi) [x]2 – 5[x] + 6 = 0
∴ ([x] – 3)([x] – 2) = 0
∴ [x] = 3 or 2
If [x] = 2, then 2 ≤ x < 3
If [x] = 3, then 3 ≤ x < 4
∴ Solution set = [2, 4)
(vii) [x – 2] + [x + 2] + {x} = 0
∴ [x] – 2 + [x] + 2 + {x} = 0
∴ [x] + x = 0 …..[{x} + [x] = x]
∴ x = 0
L.H.S. = an integer
R.H.S. = an integer
∴ x = 6k, where k is an integer
Question 40.
For f to be defined,
x – 3 ≥ 0, 5 – x > 0 and 5 – x ≠ 1
x ≥ 3, x < 5 and x ≠ 4
∴ Domain of f = [3, 4) ∪ (4, 5)
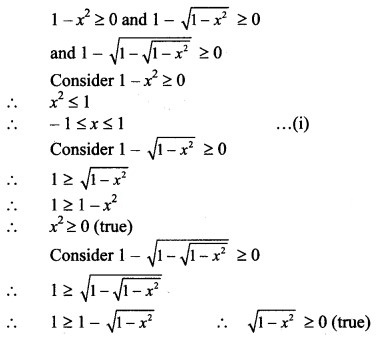
Equation (i) gives solution set = [-1, 1]
∴ Domain of f = [-1, 1]
(iv) f(x) = x!
∴ Domain of f = set of whole numbers (W)
5 – x > 0, x – 1 ≥ 0, x – 1 ≤ 5 – x
∴ x < 5, x ≥ 1 and 2x ≤ 6
∴ x ≤ 3
∴ Domain of f = {1, 2, 3}
x – x2 ≥ 0
∴ x2 – x ≤ 0
∴ x(x – 1) ≤ 0
∴ 0 ≤ x ≤ 1 …..(i)
5 – x ≥ 0
∴ x ≤ 5 …..(ii)
Intersection of intervals given in (i) and (ii) gives
Solution set = [0, 1]
∴ Domain of f = [0, 1]
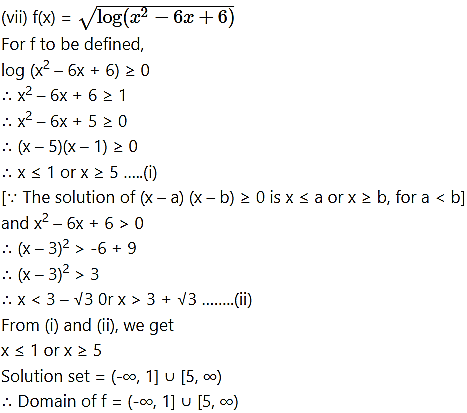
Question 41.
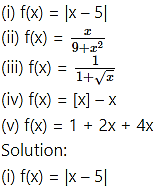
∴ Range of f = [0, ∞)
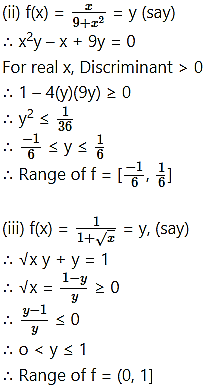
(iv) f(x) = [x] – x = -{x}
∴ Range of f = (-1, 0] …..[0 ≤ {x} < 1]
(v) f(x) = 1 + 2x + 4x
Since, 2x > 0, 4x > 0
∴ f(x) > 1
∴ Range of f = (1, ∞)
Question 42.
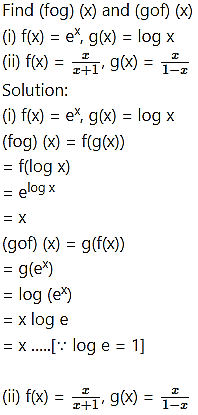
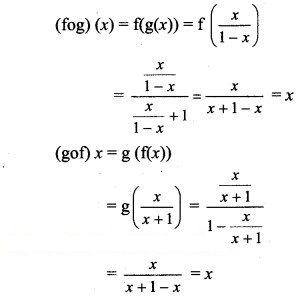
Question 43.
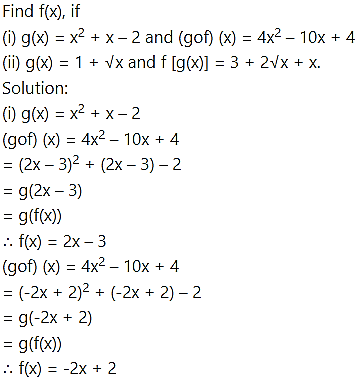
(ii) g(x) = 1 + √x
f(g(x)) = 3 + 2√x + x
= x + 2√x + 1 + 2
= (√x + 1)2 + 2
f(√x + 1) = (√x + 1)2 + 2
∴ f(x) = x2 + 2
Question 44.
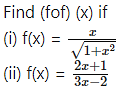
Solution:
