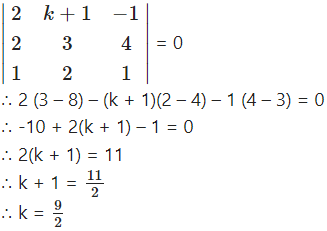Blog

Chapter 6 Line and Plane Ex 6.2

Chapter 6 Line and Plane Ex 6.2

Question 1.

Solution:
Let PM be the perpendicular drawn from the point P (2, -3, 1) to the line 

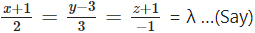
The coordinates of any point on the line are given by x = -1 + 2λ, y = 3 + 3λ, z = -1 – λ
Let the coordinates of M be
(-1 + 2λ, 3 + 3λ, -1 – λ) … (1)
The direction ratios of PM are
-1 + 2λ – 2, 3 + 3λ + 3, -1 – λ – 1
i.e. 2λ – 3, 3λ + 6, -λ – 2
The direction ratios of the given line are 2, 3, -1.
Since PM is perpendicular to the given line, we get
2(2λ – 3) + 3(3λ + 6) – 1(-λ – 2) = 0
∴ 4λ – 6 + 9λ + 18 + λ + 2 = 0
∴ 14λ + 14 = 0 ∴ λ = -1.
Put λ = -1 in (1), the coordinats of M are
(-1 – 2, 3 – 3, -1 + 1) i.e. (-3, 0,0).
∴ length of perpendicular from P to the given line

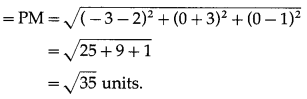
Alternative Method:


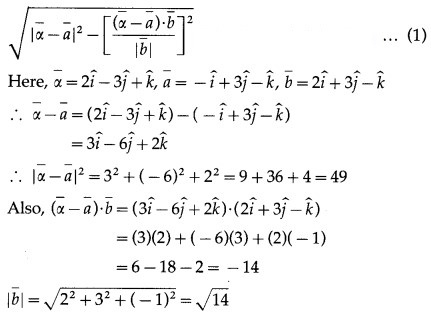
Substituting these values in (1), we get
length of perpendicular from P to given line

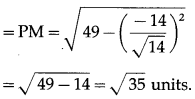
Question 2.

Solution:



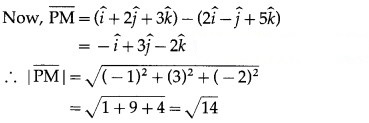
Hence, the coordinates of the foot of perpendicular are (1,2, 3) and length of perpendicular = √14 units.

Question 3.
Find the shortest distance between the

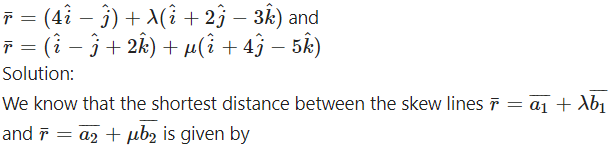
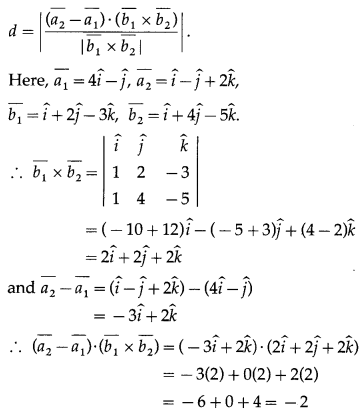
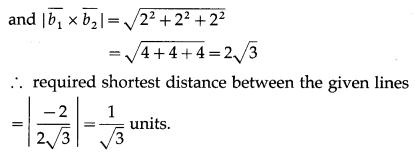
Question 4.
Solution:
The shortest distance between the lines

= 4(-6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64 = -116
and (m₁n₂ – m₂n₁)² + (l₂n₁ – l₁n₂)² + (l₁m₂ – l₂m₁)²
= (-6 + 2)² + (1 – 7)² + (-14 + 6)²
= 16 + 36 + 64 = 116

Question 5.

The coordinates of any point on the line are given by x = -1 + 2λ, y = 3 + 2λ, z = 8 – λ
Let the coordinates of M be
(-1 + 2λ, 3 + 3λ, -1 – λ) …..(1)
The direction ratios of PM are
-1 + 2λ – 2, 3 + 3λ + 3, -1 – λ – 1
i.e. 2λ – 3, 3λ = 6, -λ – 2
The direction ratios of the given line are 2, 3, 8.
Since PM is perpendicular to the given line, we get
2(2λ – 3) + 3(3λ + 6) – 1(-λ – 2) = O
∴ 4λ – 6 + 9λ + 18 + λ + 2 = 0
∴ 14λ + 14 = 0
∴ λ = -1
Put λ in (1), the coordinates of M are
(-1 – 2, 3 – 3, -1 + 1) i.e. (-3, 0, 0).
∴ length of perpendicular from P to the given line
= PM

Alternative Method :
We know that the perpendicular distance from the point

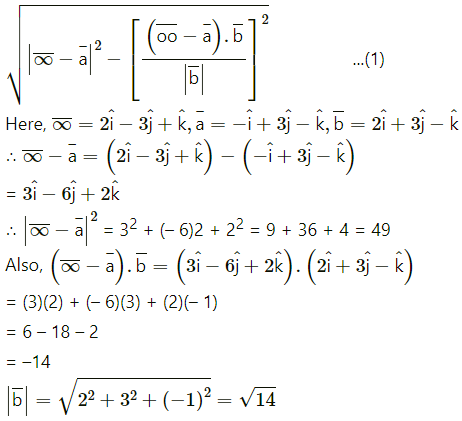
Substitutng tese values in (1), w get
length of perpendicular from P to given line
= PM

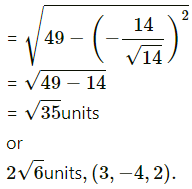
Question 6.
A(1, 0, 4), B(0, -11, 13), C(2, -3, 1) are three points and D is the foot of the perpendicular from A to BC. Find the co-ordinates of D.
Solution:
Equation of the line passing through the points (x₁, y₁, z₁) and (x₂, y₂, z₂) is

AD is the perpendicular from the point A (1, 0, 4) to the line BC.
The coordinates of any point on the line BC are given by x = 2λ, y = -11 + 8λ, z = 13 – 12λ
Let the coordinates of D be (2λ, -11 + 8λ, 13 – 12λ) … (1)
∴ the direction ratios of AD are
2λ – 1, -1λ + 8λ – 0, 13 – 12λ – 4 i.e.
2λ – 1, -11 + 8λ, 9 – 12λ
The direction ratios of the line BC are 2, 8, -12.
Since AD is perpendicular to BC, we get
2(2λ – 1) + 8(-11 + 8λ) – 12(9 – 12λ) = 0
∴ 42λ – 2 – 88 + 64λ – 108 + 144λ = 0
∴ 212λ – 198 = 0

Question 7.
By computing the shortest distance, determine whether following lines intersect each other.
Solution:
The shortest distance between the lines


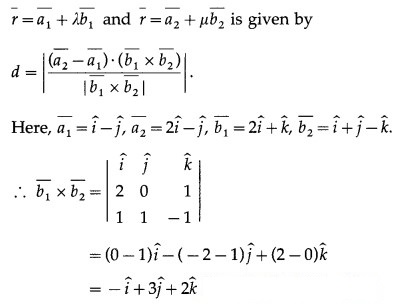
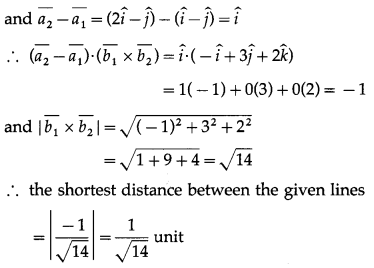
Hence, the given lines do not intersect.

Solution:
The shortest distance between the lines

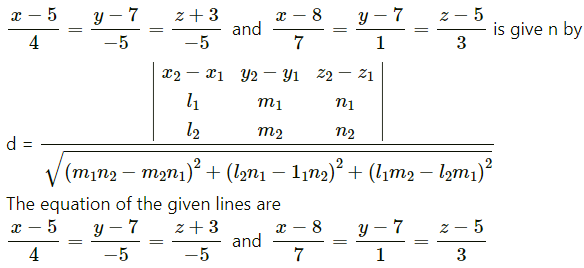
∴ x₁ = -1, y₁ = -1, z₁ = -1, x₂ = 3, y₂ = 5, z₂ = 7,
l₁ = 7, m₁ = -6, n₁ = 1, l₂ = 1, m₂ = -2, n₂ = 1

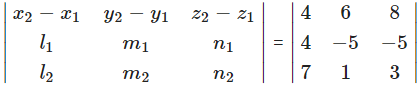
= 4(- 6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64
= -116
and
(m₁n₂ – m₂n₁)² + (l₂n₁ – l₁n₂)² + (l₁m₂ – l₂m₁)²
= (-6 + 2)² + (1 – 7)² + (-14 + 6)²
= 16 + 36 + 64
= 116
Hence, the required shortest distance between the given lines

Question 8.

Solution:
The lines

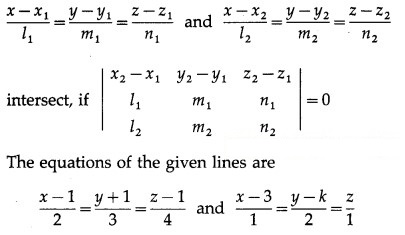
∴ x₁ = 1, y₁ = -1, z₁ = 1, x₂ = 3, y₂ = k, z₂ = 0,
l₁ = 2, m₁ = 3, n₁ = 4, l₂ = 1, m₂ = 2, n₂ = 1.
Since these lines intersect, we get