Blog

Chapter 6 Line and Plane Miscellaneous Exercise 6A

Chapter 6 Line and Plane Miscellaneous Exercise 6A

Question 1.

Question 2.

Question 3.

Question 4.

Question 5.
Find the vector equation of the line which passes through the origin and the point (5, -2, 3).
Solution:

Question 6.
Find the Cartesian equations of the line which passes through points (3, -2, -5) and (3, -2, 6).
Solution:
Let A = (3, -2, -5), B = (3, -2, 6)
The direction ratios of the line AB are
3 – 3, -2 – (-2), 6 – (-5) i.e. 0, 0, 11.
The parametric equations of the line passing through (x₁, y₁, z₁) and having direction ratios a, b, c are
x = x₁ + aλ, y = y₁ + bλ, z = z₁ + cλ
∴ the parametric equattions of the line passing through (3, -2, -5) and having direction ratios are 0, 0, 11 are
x = 3 + (0)λ, y = -2 + 0(λ), z = -5 + 11λ
i.e. x = 3, y = -2, z = 11λ – 5
∴ the cartesian equations of the line are
x = 3, y = -2, z = 11λ – 5, λ is a scalar.

Question 7.
Find the Cartesian equations of the line passing through A(3, 2, 1) and B(1, 3, 1).
Solution:
The direction ratios of the line AB are 3 – 1, 2 – 3, 1 – 1 i.e. 2, -1, 0.
The parametric equations of the line passing through (x₁, y₁, z₁) and having direction ratios a, b, c are
x = x₁ + aλ, y = y₁ + bλ, z = z₁ + cλ
∴ the parametric equattions of the line passing through (3, 2, 1) and having direction ratios 2, -1, 0 are
x = 3 + 2λ, y = 2 – λ, z = 1 + 0(λ)
x – 3 = 2λ, y – 2 = -λ, z = 1

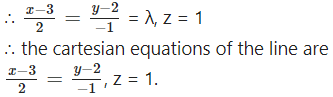
Question 8.


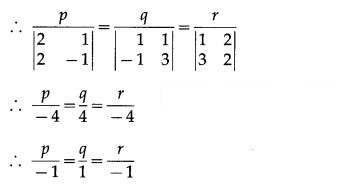
∴ the required line has direction ratios -1, 1, -1.
The cartesian equations of the line passing through (x₁, y₁, z₁) and having direction ratios a, b, c are

∴ the cartesian equations of the line passing through the point (1, 1, 2) and having direction ratios -1, 1, -1 are

Question 9.

∴ p + 2q + r = 0, 3 + 2q – r = 0

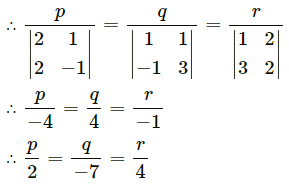
∴ the required line has direction ratios 2, -7, 4.
The cartesian equations of the line passing through (x₁, y₁, z₁) and having direction ratios a, b, c are

∴ the cartesian equation of the line passing through the point (2, -7, 4) and having directions ratios 2, -7, 4 are

Question 10.
Find the vector equation of the line which passes through the origin and intersect the line x – 1 = y – 2 = z – 3 at right angle.
Solution:

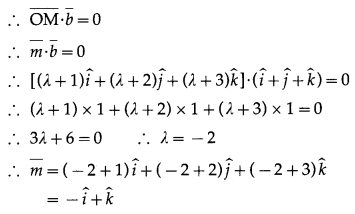
Question 11.

Solution:
The equations of the given lines are

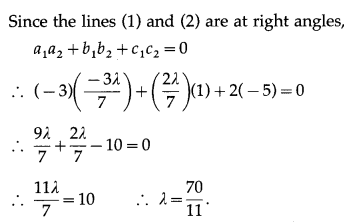
Question 12.

Solution:

Question 13.
Find the acute angle between lines x = y, z = 0 and x = 0, z = 0.
Solution:
The equations x = y, z = 0 can be written as x/1=y/1, z = 0
∴ the direction ratios of the line are 1, 1, 0.
The direction ratios of the line x = 0, z = 0, i.e., Y-axis J are 0, 1, 0.
∴ its directiton ratios are 0, 1, 0.
Let a¯ and b¯ be the vectors in the direction of the lines x = y, z = 0 and x = 0, z = 0.

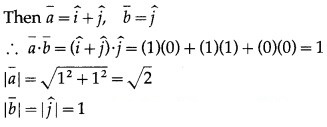
If θ is the acute angle between the lines, then

Question 14.
Find the acute angle between lines x = -y, z = 0 and x = 0, z = 0.
Solution:
The equations x = -y, z = 0 can be written as x/1=y/1, z = 0.
∴ the direction ratios of the line are 1, 1, 0.
The direction ratios of the line x = 0, z = 0, i.e., Y-axis are 0, 1, 0.
∴ its direction ratios are 0, 1, 0.
Let a¯ and b¯ be the vectors in the direction of the lines x = y, z = 0 and x = 0, z = 0

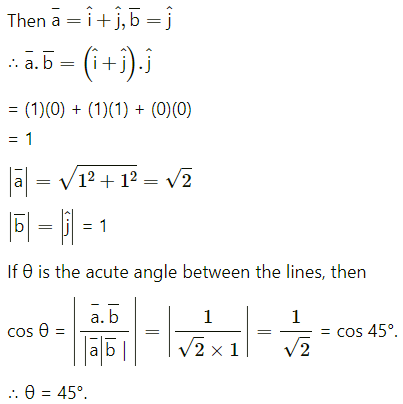
Question 15.

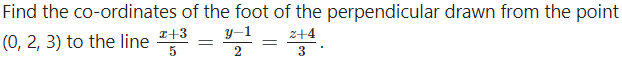
Solution:
Let P = (0, 2, 3)
Let M be the foot of the perpendicular drawn from P to the line 

The coordinates of any point on the line are given by
x = 5λ – 3, y = 2λ + 1, z = 3λ – 4
Let M = (5λ – 3, 2λ + 1, 3λ – 4) …(1)
The direction ratios of PM are
5λ – 3 – 0, 2λ + 1 – 2, 3λ – 4 – 3 i.e. 5λ – 3, 2λ – 1, 3λ – 7
Since, PM is perpendicular to the line whose direcction ratios are 5, 2, 3,
5(5λ – 3) + 2(2λ – 1) + 3(3λ – 7) = 0
25λ – 15 + 4λ – 2 + 9λ – 21 =0
38λ – 38 = 0 ∴ λ = 1
Substituting λ = 1 in (1), we get.
M = (5 – 3, 2 + 1, 3 – 4) = (2, 3, -1).
Hence, the coordinates of the foot of perpendicular are (2, 3, – 1).

Question 16.
By computing the shortest distance determine whether following lines intersect each other.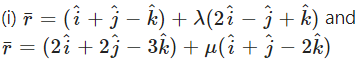

Solution:
The shortest distance between the lines


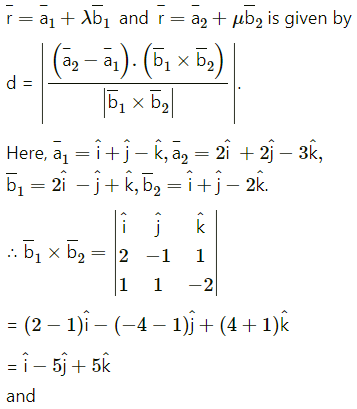
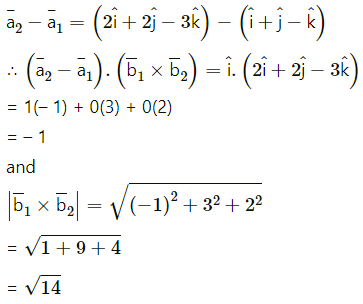
Shortest distance between the lines is 0.
∴ the lines intersect each other.

Solution:
The shortest distance between the lines

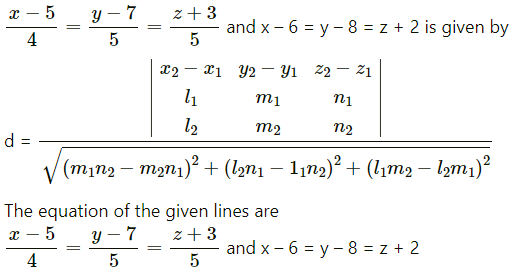
∴ x₁ = 5, y₁ = 7, z₁ = 3, x₂ = 6, y₂ = 8, z₂ = 2,
l₁ = 4, m₁ = 5, n₁ = 1, l₂ = 1, m₂ = -2, n₂ = 1

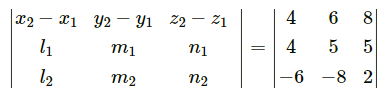
= 4(-6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64
= -116
and
(m₁n₂ – m₂n₁)² + (l₂n₁ – l₁n₂)² + (l₁m₂ – l₂m₁)²
= (-6 + 2)² + (1 – 7)² + (1 – 7)² + (-14 + 6)²
= 16 + 36 + 64
= 116
Hence, the required shortest distance between the given lines

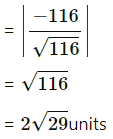
or
Shortest distance between the lines is 0.
∴ the lines intersect each other.

Question 17.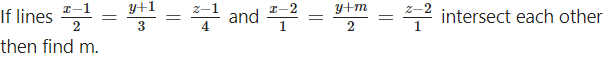

Solution:

Here, (x₁, y₁, z₁) ≡ (1, -1, 1),
(x₂, y₂, z₂) ≡ (2, -m, 2),
a₁ = 2, b₁ = 3, c₁ = 4,
a₂ = 1, b₂ = 2, c₂ = 1
Substituting these values in (1), we get

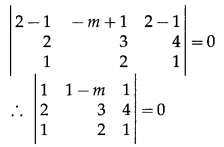
∴ 1(3 – 8) – (1 – m)(2 – 4) + 1 (4 – 3) = 0
∴ -5 + 2 – 2m + 1 = 0
∴ -2m = 2
∴ m = -1.

Question 18.
Find the vector and Cartesian equations of the line passing through the point (-1, -1, 2) and parallel to the line 2x – 2 = 3y + 1 = 6z – 2.
Solution:
Let a¯ be the position vector of the point A (-1, -1, 2) w.r.t. the origin.

The equation of given line is
x – 2 = 3y + 1 = 6z – 2.

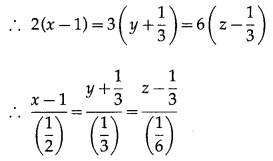
The direction ratios of this line are

Question 19.

Solution:

Question 20.

Solution:
Let the required line have direction ratios a, b, c
Since the line passes through the origin, its cartesian equations are

This line is perpendicular to the line
x – 1 = y – 2 = z – 1 whose direction ratios are 1, 1, 1.

∴ 1(4b – 3c) + 1(4a – 2c) + 1(3a – 2b) = 0
∴ 4b – 3c + 4a – 2c + 3a – 2b = 0
∴ 7a + 2b – 5c = 0
From (2) and (3), we get

Question 21.
Write the vector equation of the line whose Cartesian equations are y = 2 and 4x – 3z + 5 = 0.
Solution:
4x – 3z + 5 = 0 can be written as

Question 22.


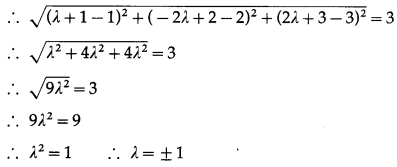
When λ = 1, M = (1 + 1, -2 + 2, 2 + 3) … [By (1)]
i. e. M = (2, 0, 5)
When λ = -1, M = (1 – 1, 2 + 2, -2 + 3) … [By (1)]
i. e. M = (0, 4, 1)
Hence, the coordinates of the required points are (2, 0, 5) and (0, 4, 1).