Chapter 7 Conic Sections Ex 7.1
Chapter 7 Conic Sections Ex 7.1
Question 1.
Find co-ordinates of focus, equation of directrix, length of latus rectum and the co-ordinates of end points of latus rectum of the parabola:

(ii) Given equation of the parabola is = -20x.
Comparing this equation with = -4ax, we get
⇒ 4a = 20
⇒ a = 5
Co-ordinates of focus are S(-a, 0), i.e., S(-5, 0)
Equation of the directrix is x – a = 0
⇒ x – 5 = 0
Length of latus rectum = 4a = 4(5) = 20
Co-ordinates of end points of latus rectum are (-a, 2a) and (-a, -2a),
⇒ (-5, 10) and (-5, -10).

(iv) Given equation of the parabola is = -8y.
Comparing this equation with = -4by, we get
⇒ 4b = 8
⇒ b = 2
Co-ordinates of focus are S(0, -b), i.e., S(0, – 2)
Equation of the directrix is y – b = 0, i.e., y – 2 = 0
Length of latus rectum = 4b = 4(2) = 8
∴ Co-ordinates of end points of latus rectum are (2b, -b) and (-2b, -b), i.e., (4, -2) and (-4, -2).

Question 2.
Find the equation of the parabola with vertex at the origin, the axis along the Y-axis, and passing through the point (-10, -5).
Solution:

Question 3.
Find the equation of the parabola with vertex at the origin, the axis along the X-axis, and passing through the point (3, 4).
Solution:

Question 4.
Find the equation of the parabola whose vertex is O(0, 0) and focus at (-7, 0).
Solution:
Focus of the parabola is S(-7, 0) and vertex is O(0, 0).
Since focus lies on X-axis, it is the axis of the parabola.
Focus S(-7, 0) lies on the left-hand side of the origin.
It is a left-handed parabola.
Required parabola is y = -4ax.
Focus is S(-a, 0).
a = 7
∴ The required equation of the parabola is =-4(7)x, i.e., = -28x.
Question 5.
Find the equation of the parabola with vertex at the origin, the axis along X-axis, and passing through the point
(i) (1, -6)
(ii) (2, 3)
Solution:
(i) Vertex of the parabola is at origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either = 4ax or = -4ax.
Since the parabola passes through (1, -6), it lies in the 4th quadrant.
Required parabola is = 4ax.
Substituting x = 1 and y = -6 in = 4ax, we get
⇒ (-6 = 4a(1)
⇒ 36 = 4a
⇒ a = 9
∴ The required equation of the parabola is = 4(9)x, i.e., = 36x.

Question 6.

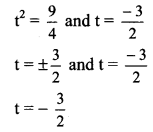


∴ The parameter of the given point is −92
Question 7.
Find the focal distance of a point on the parabola = 16x whose ordinate is 2 times the abscissa.
Solution:
Given the equation of the parabola is = 16x.
Comparing this equation with = 4ax, we get
⇒ 4a = 16
⇒ a = 4
Since ordinate is 2 times the abscissa,
y = 2x
Substituting y = 2x in = 16x, we get
⇒ (2x = 16x
⇒ 4 = 16x
⇒ 4 – 16x = 0
⇒ 4x(x – 4) = 0
⇒ x = 0 or x = 4
When x = 4,
focal distance = x + a = 4 + 4 = 8
When x = 0,
focal distance = a = 4
∴ Focal distance is 4 or 8.
Question 8.
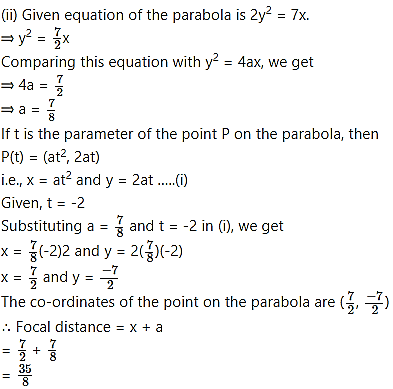
Question 9.
For the parabola = 4x, find the coordinates of the point whose focal distance is 17.
Solution:
Given the equation of the parabola is = 4x.
Comparing this equation with = 4ax, we get
⇒ 4a = 4
⇒ a = 1
Focal distance of a point = x + a
Given, focal distance = 17
⇒ x + 1 = 17
⇒ x = 16
Substituting x = 16 in y2 = 4x, we get
⇒ = 4(16)
⇒ = 64
⇒ y = ±8
∴ The co-ordinates of the point on the parabola are (16, 8) or (16, -8).
Question 10.
Find the length of the latus rectum of the parabola = 4ax passing through the point (2, -6).
Solution:
Given equation of the parabola is = 4ax and it passes through point (2, -6).
Substituting x = 2 and y = -6 in = 4ax, we get
⇒ (-6 = 4a(2)
⇒ 4a = 18
∴ Length of latus rectum = 4a = 18 units
Question 11.
Find the area of the triangle formed by the line joining the vertex of the parabola = 12y to the endpoints of the latus rectum.
Solution:
Given the equation of the parabola is = 12y.
Comparing this equation with = 4by, we get
⇒ 4b = 12
⇒ b = 3
The co-ordinates of focus are S(0, b), i.e., S(0, 3)
End points of the latus-rectum are L(2b, b) and L'(-2b, b),
i.e., L(6, 3) and L'(-6, 3)
Also l(LL’) = length of latus-rectum = 4b = 12
l(OS) = b = 3
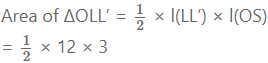
Area of ∆OLL’ = 18 sq. units
Question 12.
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
Solution:
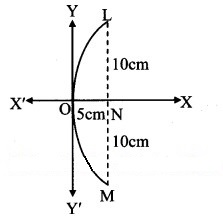
Let LOM be the parabolic reflector such that LM is the diameter and ON is its depth.
It is given that ON = 5 cm and LM = 20 cm.
LN = 10 cm
Taking O as the origin, ON along X-axis and a line through O ⊥ ON as Y-axis.
Let the equation of the reflector be = 4ax ……(i)
The point L has the co-ordinates (5, 10) and lies on parabola given by (i).
Substituting x = 5 and y = 10 in (i), we get
⇒ 1 = 4a(5)
⇒ 100 = 20a
⇒ a = 5
Focus is at (a, 0), i.e., (5, 0)
Question 13.
Find co-ordinates of focus, vertex, and equation of directrix and the axis of the parabola y = – 2x + 3.
Solution:

⇒ 4y – 7 = 0
Question 14.
Find the equation of tangent to the parabola


Question 15.

Alternate method:
We know that, tangents drawn from a point on directrix are perpendicular.
(-6, 9) lies on the directrix x = -a.
⇒ -6 = -a
⇒ a = 6
Since 4a = k
⇒ k = 4(6) = 24
Question 16.

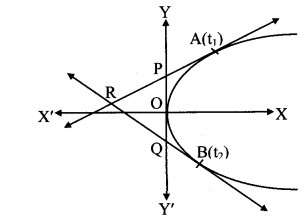
A tangent at the vertex is Y-axis whose equation is x = 0.
x-coordinate of points P and Q is 0.
Let P be(0, ) and Q be (0, ).
Then, from (i) and (ii), we get

∴ Equation of locus of R is = 8(x + 2).
Question 17.
Find the equation of common tangent to the parabolas = 4x and = 32y.
Solution:
Given equation of the parabola is = 4x
Comparing this equation with = 4ax, we get
⇒ 4a = 4
⇒ a = 1

⇒ x + 2y + 4 = 0, which is the equation of the common tangent.
Question 18.
Find the equation of the locus of a point, the tangents from which to the parabola = 18x are such that sum of their slopes is -3.
Solution:
Given equation of the parabola is = 18x
Comparing this equation with = 4ax, we get
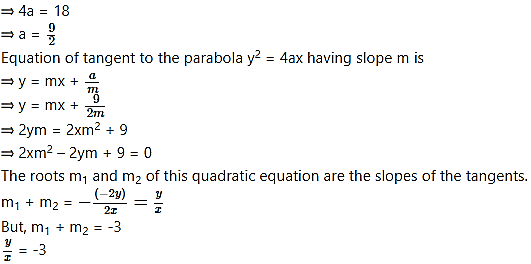
y = -3x, which is the required equation of locus.
Question 19.
The towers of a bridge, hung in the form of a parabola, have their tops 30 metres above the roadway and are 200 metres apart. If the cable is 5 metres above the roadway at the centre of the bridge, find the length of the vertical supporting cable 30 metres from the centre.
Solution:
Let CAB be the cable of the bridge and X’OX be the roadway.
Let A be the centre of the bridge.
From the figure, vertex of parabola is at A(0, 5).
Let the equation of parabola be

The length of the vertical supporting cable is 7.25 m.
Question 20.
A circle whose centre is (4, -1) passes through the focus of the parabola + 16y = 0. Show that the circle touches the directrix of the parabola.
Solution:
Given equation of the parabola is + 16y = 0.
⇒ = -16y
Comparing this equation with = -4by, we get
⇒ 4b = 16
⇒ b = 4
Focus = S(0, -b) = (0, -4)
Centre of the circle is C(4, -1) and it passes through focus S of the parabola.

= radius
∴ The circle touches the directrix of the parabola.