Chapter 7 Linear Programming Ex 7.2
Chapter 7 Linear Programming Ex 7.2
I) Find the feasible solution of the following inequations graphically.
Question 1.
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CD whose equations are 3x + 2y = 18 and 2x + y = 10 respectively.
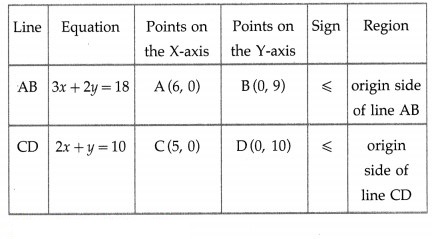
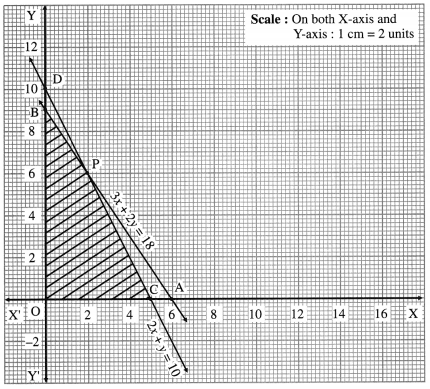
The feasible solution is OCPBO which is shaded in the graph.
Question 2.
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CB whose equations are 2x + 3y = 6 and x + y = 2 respectively.
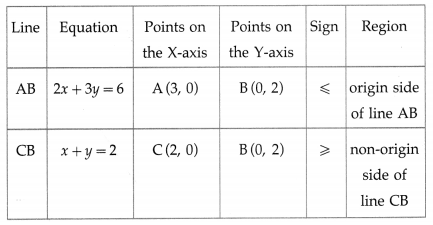
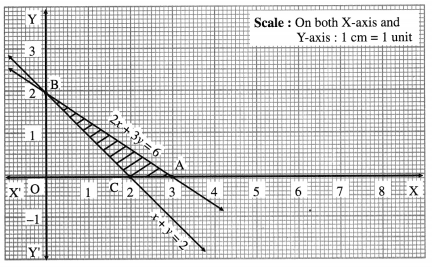
The feasible solution is ∆ABC which is shaded in the graph.
Question 3.
3x + 4y ≥ 12, 4x + 7y ≤ 28, y ≥ 1, x ≥ 0
Solution:
First we draw the lines AB, CD and EF whose equations are 3x + 4 y = 12, 4x + 7y = 28 and y = 1 respectively.
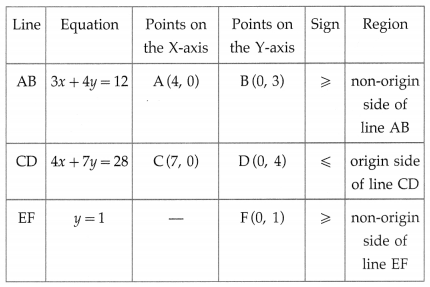
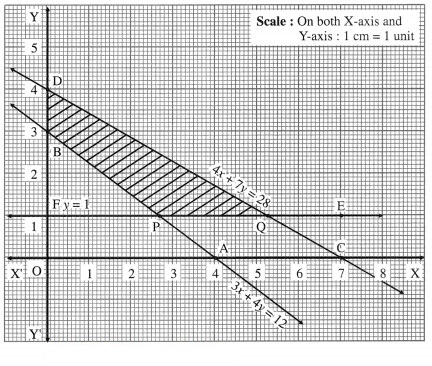
The feasible solution is PQDBP. which is shaded in the graph.
Question 4.
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.
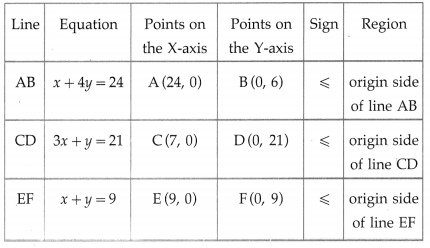
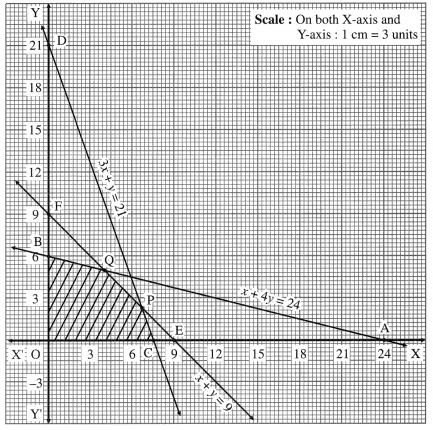
The feasible solution is OCPQBO. which is shaded in the graph.
Question 5.
0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≤ 5, 2x + y ≥ 4
Solution:
First we draw the lines AB, CD, EF and GH whose equations are x + y = 5, 2x + y = 4, x = 3 and y = 3 respectively.
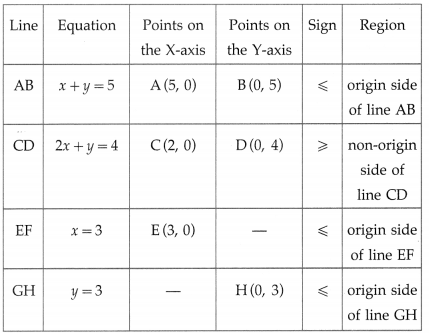
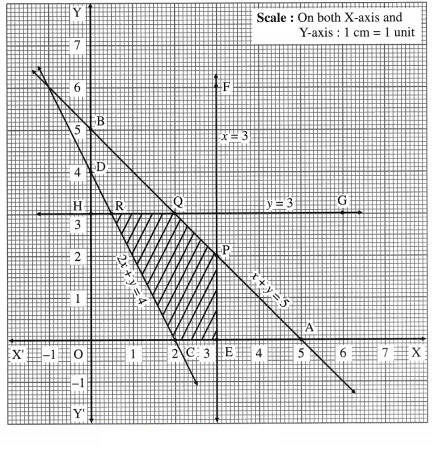
The feasible solution is CEPQRC. which is shaded in the graph.
Question 6.
x – 2y ≤ 2, x + y ≥ 3, -2x + y ≤ 4, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB, CD and EF whose equations are x – 2y = 2, x + y = 3 and -2x + y = 4 respectively.
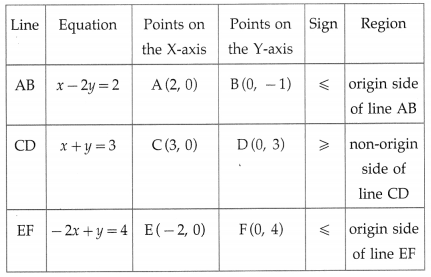
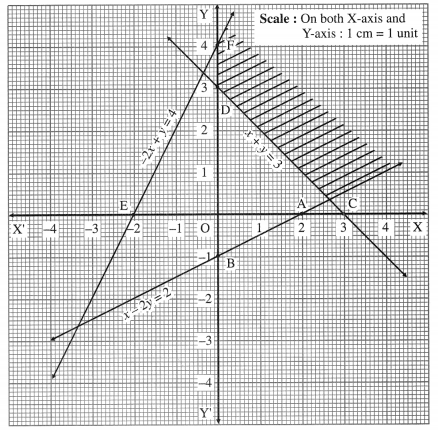
The feasible solution is shaded in the graph.
Question 7.
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find the feasible solution graphically.
Solution:
Let the company produces x units of article A and y units of article B.
The given data can be tabulated as:
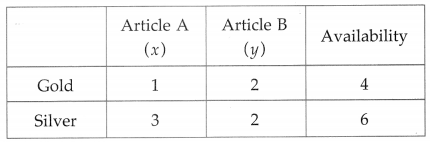
Inequations are :
x + 2y ≤ 4 and 3x + 2y ≤ 6
x and y are number of items, x ≥ 0, y ≥ 0
First we draw the lines AB and CD whose equations are x + 2y = 4 and 3x + 2y = 6 respectively.
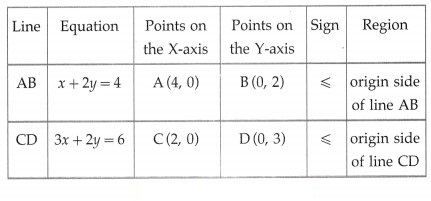
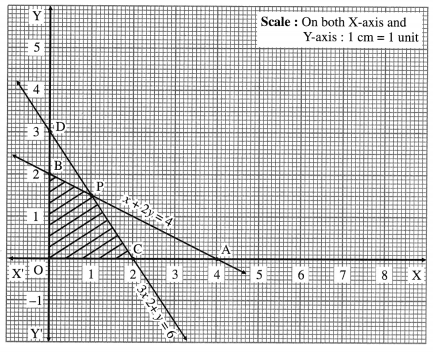
The feasible solution is OCPBO. which is shaded in the graph.
Question 8.
A furniture dealer deals in tables and chairs. He has Rs.1,50,000 to invest and a space to store at most 60 pieces. A table costs him Rs.1500 and a chair Rs.750. Construct the inequations and find the feasible solution.
Question is modified
A furniture dealer deals in tables and chairs. He has ₹ 15,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 150 and a chair ₹ 750. Construct the inequations and find the feasible solution.
Solution:
Let x be the number of tables and y be the number of chairs. Then x ≥ 0, y ≥ 0.
The dealer has a space to store at most 60 pieces.
∴ x + y ≤ 60
Since, the cost of each table is ₹ 150 and that of each chair is ₹ 750, the total cost of x tables and y chairs is 150x + 750y. Since the dealer has ₹ 15,000 to invest, 150x + 750y ≤ 15,000
Hence the system of inequations are
x + y ≤ 60, 150x + 750y ≤ 15000, x ≥ 0, y ≥ 0.
First we draw the lines AB and CD whose equations are x + y = 60 and 150x + 750y = 15,000 respectively.
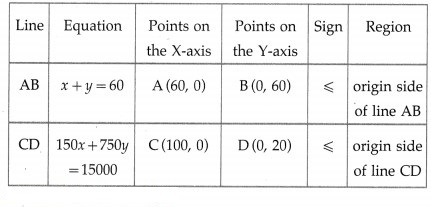
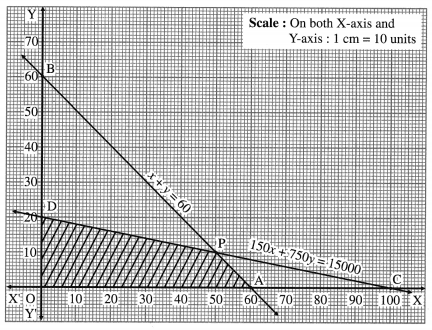
The feasible solution is OAPDO. which is shaded in the graph.