Chapter 7 Mensuration Set 7.2
Chapter 7 Mensuration Set 7.2
Question 1.
The radii of two circular ends of frustum shaped bucket are 14 cm and 7 cm. Height of the bucket is 30 cm. How many litres of water it can hold? (1 litre = 1000 cm3)
Given: Radii (r1) = 14 cm, and (r2) = 7 cm,
height (h) = 30 cm
To find: Amount of water the bucket can hold.
Solution:
Volume of frustum = 13 πh (r12 + r22 + r1 × r2)
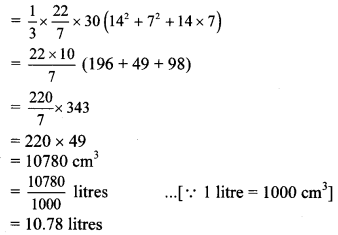
∴ The bucket can hold 10.78 litres of water.
Question 2.
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its
i. curved surface area,
ii. total surface area,
iii. volume, (π = 3.14)
Given: Radii (r1) = 14 cm, and (r2) = 6 cm,
height (h) = 6 cm
Solution:

i. Curved surface area of frustum
= πl (r1 + r2)
= 3.14 × 10(14 + 6)
= 3.14 × 10 × 20 = 628 cm2
∴ The curved surface area of the frustum is 628 cm2.
ii. Total surface area of frustum
= πl (r1+ r2) + πr12 + πr22
= 628 + 3.14 × (14)2 + 3.14 × (6)2
= 628 + 3.14 × 196 + 3.14 × 36
= 628 + 3.14(196 + 36)
= 628 + 3.14 × 232
= 628 + 728.48
= 1356.48 cm2
∴ The total surface area of the frustum is 1356.48 cm2.
iii. Volume of frustum
= 1/3 πth(r12 +r22 + r1 × r2)
= 1/3 × 3.14 × 6(142 + 62 + 14 × 6)
= 3.14 × 2(196 + 36 + 84)
= 3.14 × 2 × 316
= 1984.48 cm3
∴ The volume of the frustum is 1984.48 cm3.
Question 3.
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of frustum, complete the following activity. (π = 22/7 )
Solution:
Circumference1 = 27πr1 = 132 cm

Curved surface area of frustum = π (r1 + r2) l
= π (21 + 14) × 25
=π × 35 × 35
= 22/7 × 35 × 25
= 2750 cm2