Chapter 8 Continuity Miscellaneous Exercise 8
Chapter 8 Continuity Miscellaneous Exercise 8
(I) Select the correct answer from the given alternatives.
Question 1.

Hint:

Question 2.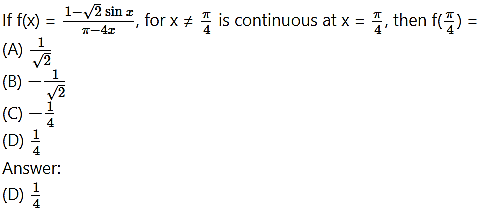
Hint:


Question 3.

Hint:

Question 4.![]()
(A) f is discontinuous at x = 2
(B) f is discontinuous at x = -4
(C) f is discontinuous at x = 0
(D) f is discontinuous at x = 2 and x = -4
Answer:
(B) f is discontinuous at x = -4
Hint:

Here f(x) is a rational function and is continuous everywhere except at the points Where denominator becomes zero.
Here, denominator becomes zero when x = -4 or x = 2
But x = 2 does not lie in the given interval.
∴ x = -4 is the point of discontinuity.
Question 5.
If f(x) = ax2 + bx + 1, for |x – 1| ≥ 3 and
= 4x + 5, for -2 < x < 4
is continuous everywhere then,

Hint:
f(x) = ax2 + bx + 1, |x – 1| ≥ 3
= 4x + 5; -2 < x < 4
The first interval is
|x – 1| ≥ 3
∴ x – 1 ≥ 3 or x – 1 ≤ -3
∴ x ≥ 4 or x ≤ -2
∴ f(x) is same for x ≤ -2 as well as x ≥ 4.
∴ f(x) is defined as:
f(x) = ax2 + bx + 1; x ≤ -2
= 4x + 5; -2 < x < 4
= ax2 + bx + 1; x ≥ 4
f(x) is continuous everywhere.
∴ f(x) is continuous at x = -2 and x = 4.
As f(x) is continuous at x = -2,

∴ a(-2)2 + b(-2) + 1 = 4(-2) + 5
∴ 4a – 2b + 1 = -3
∴ 4a – 2b = -4
∴ 2a – b = -2 …..(i)
∵ f(x) is continuous at x = 4,

4(4) + 5 = a(4)2 + b(4) + 1
16a + 4b + 1 = 21
16a + 4b = 20
4a + b = 5 …..(ii)
Adding (i) and (ii), we get
6a = 3
∴ a = 1/2
Substituting a = 12 in (ii), we get
4(1/2) + b = 5
∴ 2 + b = 5
∴ b = 3
∴ a =1/2, b = 3
Question 6.

Hint:

Question 7.![]()
= k, for x = 0,
is continuous at x = 0, then value of ‘k’ is
(A) 6
(B) 4
(C) (log 2) (log 4)
(D) 3 log 4
Answer:
(A) 6
Hint:


Question 8.
(D) None of these
Answer:
(B) log 2 . log 3
Hint:

Question 9.

Hint:


Question 10.
If f(x) = ⌊x⌋ for x ∈ (-1, 2), then f is discontinuous at
(A) x = -1, 0, 1, 2
(B) x = -1, 0, 1
(C) x = 0, 1
(D) x = 2
Answer:
(C) x = 0, 1
Hint:
f(x) = ⌊x⌋, x ∈ (-1, 2)
This function is discontinuous at all integer values of x between -1 and 2.
∴ f(x) is discontinuous at x = 0 and x = 1.
II. Discuss the continuity of the following functions at the point(s) or on the interval indicated against them.
Question 1.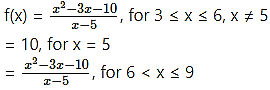
Solution:

Question 2.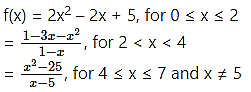
= 7, for x = 5
Solution:
The domain of f(x) is [0, 7].
(i) For 0 ≤ x ≤ 2
f(x) = 2x2 – 2x + 5
It is a polynomial function and is Continuous at all point in [0, 2).
(ii) For 2 < x < 4
![]()
It is a rational function and is continuous everwhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 1
But x = 1 does not lie in the interval.
f(x) is continuous at all points in (2, 4).
(iii) For 4 ≤ x ≤ 7, x ≤ 5
![]()
It is a rational function and is continuous everywhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 5
But x = 5 does not lie in the interval.
∴ f(x) is continuous at all points in (4, 7] – {5}.
(iv) For continuity at x = 2:

∴ f(x) is continuous at x = 2.
(v) For continuity at x = 4:

∴ f(x) is continuous at x = 4.
(vi) For continuity at x = 5.
f(5) = 7

∴ f(x) is discontinuous at x = 5.
Thus, f(x) is continuous at all points on its domain except at x = 5.
Question 3.

It is a rational function and is continuous everywhere except at points where its denominator becomes zero.
Denominator becomes zero when cos x = 1,
i.e., x = 0
But x = 0 does not lie in the interval.
![]()
(ii) For continuity at x = 0:


∴ f(x)≠f(0)
∴ f(x) is discontinuous at x = 0.
Question 4.

Solution:

Question 5.![]()
= 0, for x = -1, at x = -1
Solution:


Question 6.
f(x) = [x + 1] for x ∈ [-2, 2)
Where [*] is greatest integer function.
Solution:
f(x) = [x + 1], x ∈ [-2, 2)
∴ f(x) = -1, x ∈ [-2, -1)
= 0, x ∈ [-1, 0)
= 1, x ∈ [0, 1)
= 2, x ∈ [1, 2)

![]()
∴ f(x) is discontinuous at x = -1.
Similarly, f(x) is discontinuous at the points x = 0 and x = 1.
Question 7.
f(x) = 2x2 + x + 1, for |x – 3| ≥ 2
= x2 + 3, for 1 < x < 5
Solution:
|x – 3| ≥ 2
∴ x – 3 ≥ 2 or x – 3 ≤ -2
∴ x ≥ 5 or x ≤ 1
∴ f(x) = 2x2 + x + 1, x ≤ 1
= x2 + 3, 1 < x < 5
= 2x2 + x + 1, x ≥ 5
Consider the intervals
x < 1 , i.e., (-∞, 1)
1 < x < 5, i.e., (1, 5) x > 5, i.e., (5, ∞)
In all these intervals, f(x) is a polynomial function and hence is continuous at all points.
For continuity at x = 1:

∴ f(x) is discontinuous at x = 5.
∴ f(x) is continuous for all x ∈ R, except at x = 5.
III. Identify discontinuities if any for the following functions as either a jump or a removable discontinuity on their respective domains.
Question 1.

Question 2.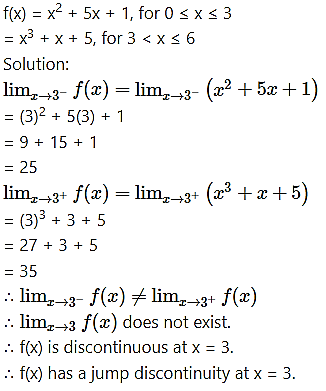
Question 3.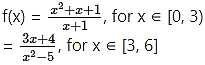
Solution:


∴ f(x) is continuous at x = 3.
IV. Discuss the continuity of the following functions at the point or on the interval indicated against them. If the function is discontinuous, identify the type of discontinuity and state whether the discontinuity is removable. If it has a removable discontinuity, redefine the function so that it becomes continuous.
Question 1.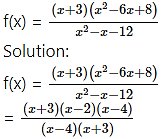
∴ f(x) is not defined at x = 4 and x = -3.
∴ The domain of function f = R – {-3, 4}.
For x ≠ -3 and 4,

f(x) is discontinuous at x = 4 and x = -3.
This discontinuity is removable.
∴ f(x) can be redefined as
![]()
= -5, for x ∈ R – {-3, 4}, x = -3
= 2, for x ∈ R – {-3, 4}, x = 4
Question 2.
f(x) = x2 + 2x + 5, for x ≤ 3
= x3 – 2x2 – 5, for x > 3
Solution:

∴ f(x) is discontinuous at x = 3.
This discontinuity is irremovable.
V. Find k if the following functions are continuous at the points indicated against them.
Question 1.![]()
= k, for x = 2 at x = 2.
Solution:
f(x) is continuous at x = 2. …..(given)


Question 2.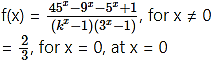
Solution:
f(x) is continuous at x = 0 …..(given)


VI. Find a and b if the following functions are continuous at the points or on the interval indicated against them.
Question 1.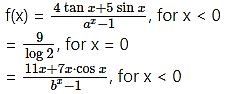
Solution:


Question 2.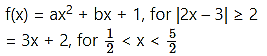
Solution:



VII. Find f(a), if f is continuous at x = a where,
Question 1.![]()
Solution:


Question 2.![]()
Solution:

VIII. Solve using intermediate value theorem.
Question 1.
Show that 5x – 6x = 0 has a root in [1, 2].
Solution:
Let f(x) = 5x – 6x
5x and 6x are continuous functions for all x ∈ R.
∴ 5x – 6x is also continuous for all x ∈ R.
i.e., f(x) is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(1) = 51 – 6(1) = -1 < 0
f(2) = (5)2 – 6(2) = 13 > 0
∴ f(1) < 0 and f(2) > 0
∴ By intermediate value theorem, there has to be a point ‘c’ between 1 and 2 such that f(c) = 0.
∴ There is a root of the given equation in [1, 2].
Question 2.
Show that x3 – 5x2 + 3x + 6 = 0 has at least two real roots between x = 1 and x = 5.
Solution:
Let f(x) = x3 – 5x2 + 3x + 6
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
Here, we have been asked to show that f(x) has at least two roots between x = 1 and x = 5.

= 27 – 45 + 9 + 6
= -3 < 0
f(4) = (4)3 – 5(4)2 + 3(4) + 6
= 64 – 80 + 12 + 6
= 2 > 0
∴ f(3) < 0 and f(4) > 0
∴ By intermediate value theorem, there has to be a point ‘c’ between 3 and 4 such that f(c) = 0.
∴ There are two roots, x = 2 and a root between x = 3 and x = 4.
Thus, there are at least two roots of the given equation between x = 1 and x = 5.