Blog

Chapter 8 Trigonometry Practice Set 8

Chapter 8 Trigonometry Practice Set 8

Question 1.
Choose the correct alternative answer for the following multiple choice questions.

i. Which of the following statements is true?
(A) sin θ = cos (90 – θ)
(B) cos θ = tan (90 – θ)
(C) sin θ = tan (90 – θ)
(D) tan θ = tan (90 – θ)
Answer:
(A) sin θ = cos (90 – θ)

ii. Which of the following is the value of sin 90°?

Answer:
(D) 1

iii. 2 tan 45° + cos 45° – sin 45° = ?
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
2 tan 45° + cos 45° – sin

(C) 2

(A) 2
(B) -1
(C) 0
(D) 1
Answer:
cos28∘sin62∘

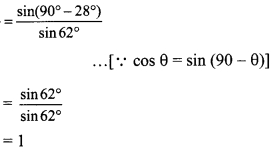
(D) 1

Question 2.
In right angled ∆TSU, TS = 5, ∠S = 90°, SU = 12, then find sin T, cos T, tan T. Similarly find sin U, cos U, tan U.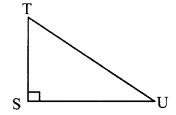

Solution:
i. TS = 5, SU = 12 …[Given]
In ∆TSU, ∠S = 90° … [Given]
∴ TU² = TS² + SU² …[Pythagoras theorem]
= 5² + 12² = 25 + 144 = 169

= 13

Question 3.
In right angled ∆YXZ, ∠X = 90°, XZ = 8 cm, YZ = 17 cm, find sin Y, cos Y, tan Y, sin Z, cos Z, tan Z.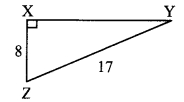

Solution:
i. XZ = 8 cm, YZ = 17 cm …[Given]
In ∆YXZ, ∠X = 90° … [Given]
∴ YZ² = XY² + XZ² .. .[Pythagoras theorem]
∴ 17² = XY² + 8²
∴ 289 = XY² + 64
∴ XY² = 289 – 64
= 225

= 15

Question 4.


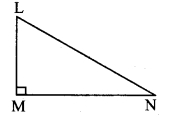
Solution:

In ∆LMN, ∠M = 90°, ∠N = θ

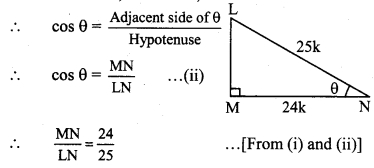
Let the common multiple be k.
∴ MN = 24k and LN = 25k
Now, LN²= LM² + MN² … [Pythagoras theorem]
∴ (25k)² = LM² + (24k)²
∴ 625 k² = LM² + 576k²
∴ LM² = 625k² – 576k²
∴ LM² = 49k²

= 7k

Question 5.
Fill in the blanks.
i. sin 20° = cos
ii. tan 30° x tan  = 1
iii. cos 40° = sin
Solution:
i. sin 20° = cos (90° – 20°) …..[∵ sin θ = cos (90 – θ)]
= cos 70°

ii. tan θ x tan (90 – θ) = 1
Substituting θ = 30°,
tan 30° x tan (90 – 30)° = 1
∴ tan 30° x tan 60° = 1

iii. cos 40° = sin (90° – 40°) …[∵ COS θ = sin (90 – θ)]
= sin 50°

Question 1.
Measuring height of a tree using trigonometric ratios. (Textbook pg. no. 101)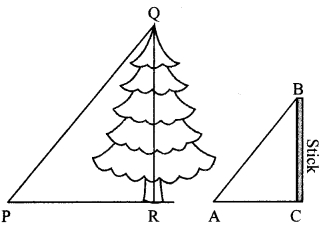

This experiment can be conducted on a clear sunny day. Look at the figure given above. Height of the tree is QR, height of the stick is BC.
Thrust a stick in the ground as shown in the figure. Measure its height and length of its shadow. Also measure the length of the shadow of the tree. Using these values, how will you determine the height of the tree?
Solution:
Rays of sunlight are parallel.
So, ∆PQR and ∆ABC are equiangular i.e., similar triangles.
Sides of similar triangles are proportional.

Substituting the values of PR, BC and AC in the above equation, we can get length of QR i.e., the height of the tree.

Question 2.
It is convenient to do the above experiment between 11:30 am and 1:30 pm instead of doing it in the morning at 8’O clock. Can you tell why? (Textbook pg. no. 101)
Solution:
At 8’O clock in the morning, the sunlight is not very bright. At the same time, the sun is on the horizon and the shadow would by very long. It would be extremely difficult to measure shadow in that case.
Between 11:30 am and 1:30 pm, the sun is overhead and it would be easier to measure the length of shadow.

Question 3.
Conduct the above discussed activity and find the height of a tall tree in your surrounding. If there is no tree in the premises, then find the height of a pole. (Textbook pg. no. 101)