Chapter 9 Differentiation Ex 9.2

Chapter 9 Differentiation Ex 9.2

(I) Differentiate the following w.r.t. x

Question 1.

Solution:

Question 2.
y = √x + tan x – x³
Solution:

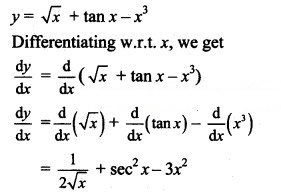
Question 3.

Solution:

Question 4.

Solution:

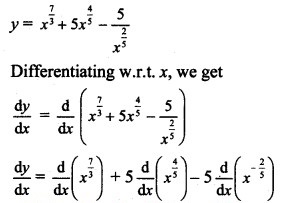
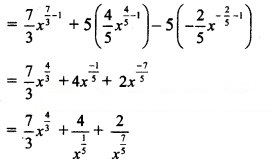
Question 5.

Solution:

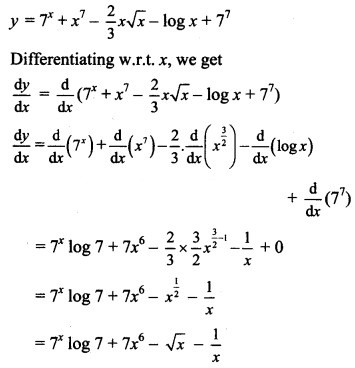
Question 6.

Solution:

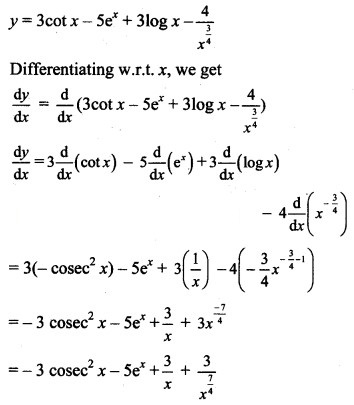
(II) Diffrentiate the following w.r.t. x

Question 1.
y = x⁵ tan x
Solution:

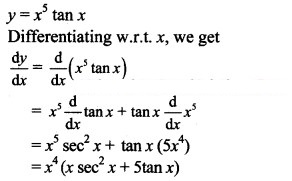
Question 2.
y = x⁵ log x
Solution:

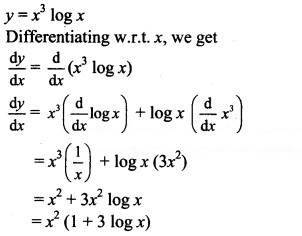
Question 3.
y = (x² + 2)² sin x
Solution:

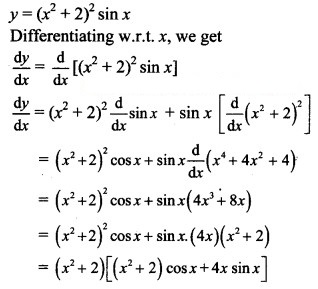
Question 4.
y = e^x log x
Solution:

Question 5.

Solution:

Question 6.

Solution:

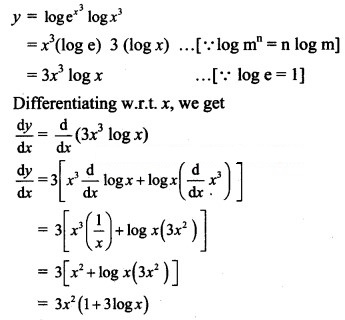
(III) Diffrentiate the following w.r.t. x

Question 1.
y = x²√x + x⁴ log x
Solution:

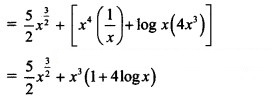
Question 2.

Solution:

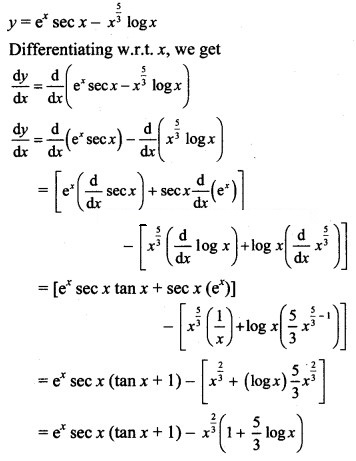
Question 3.
y = x⁴ + x√x cos x – x² e^x
Solution:

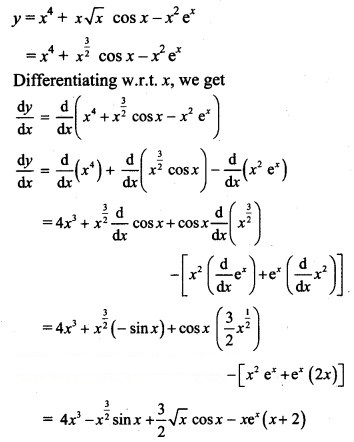
Question 4.
y = (x³ – 2) tan x – x cos x + 7^x . x⁷
Solution:

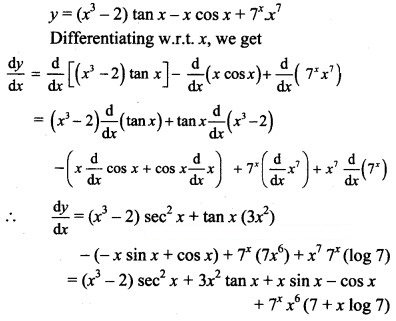
Question 5.
y = sin x log x + e^x cos x – e^x √x
Solution:

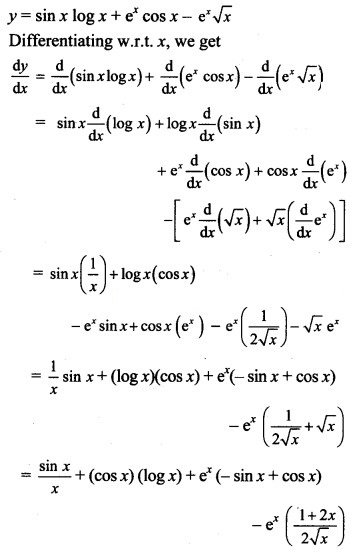
Question 6.
y = e^x tan x + cos x log x – √x 5^x
Solution:

(IV) Differentiate the following w.r.t.x.

Question 1.

Solution:

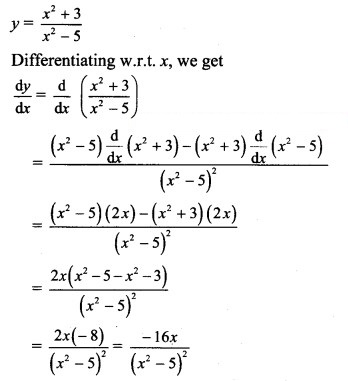
Question 2.

Solution:

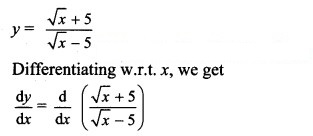
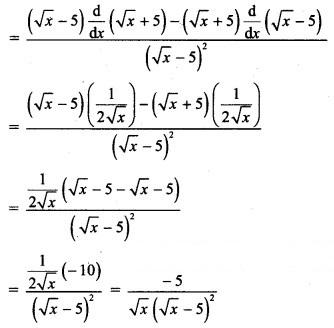
Question 3.

Solution:

Question 4.

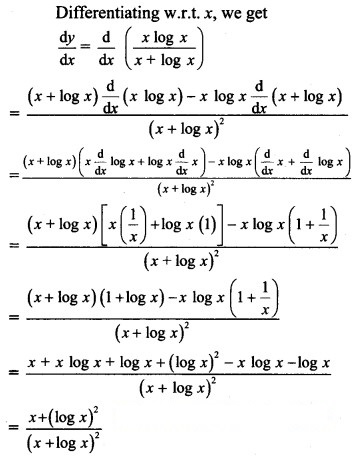
Question 5.

Solution:

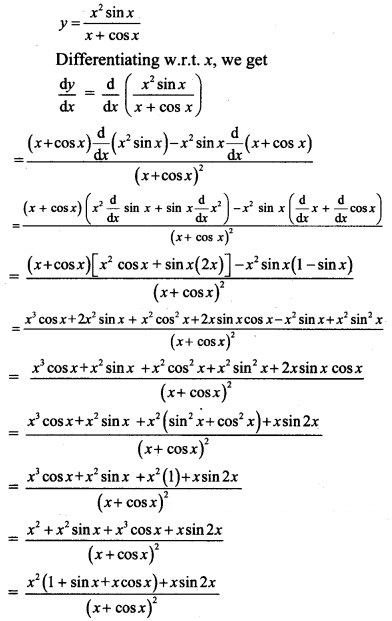
Question 6.

Solution:

(V).

Question 1.
If f(x) is a quadratic polynomial such that f(0) = 3, f'(2) = 2 and f'(3) = 12, then find f(x).
Solution:
Let f(x) = ax² + bx + c …..(i)
∴ f(0) = a(0)² + b(0) + c
∴ f(0) = c
But, f(0) = 3 …..(given)
∴ c = 3 …..(ii)
Differentiating (i) w.r.t. x, we get
f'(x) = 2ax + b
∴ f'(2) = 2a(2) + b
∴ f'(2) = 4a + b
But, f'(2) = 2 …..(given)
∴ 4a + b = 2 …..(iii)
Also, f'(3) = 2a(3) + b
∴ f'(3) = 6a + b
But, f'(3) = 12 …..(given)
∴ 6a + b = 12 …..(iv)
equation (iv) – equation (iii), we get
2a = 10
∴ a = 5
Substituting a = 5 in (iii), we get
4(5) + b = 2
∴ b = -18
∴ a = 5, b = -18, c = 3
∴ f(x) = 5x² – 18x + 3

Check:
If f(0) = 3, f'(2) = 2 and f'(3) = 12, then our answer is correct.
f(x) = 5x² – 18x + 3 and f'(x) = 10x – 18
f(0) = 5(0)² – 18(0) + 3 = 3
f'(2) = 10(2) – 18 = 2
f'(3) = 10(3) – 18 = 12
Thus, our answer is correct.

Question 2.

Solution:
f(x) = a sin x – b cos x
Differentiating w.r.t. x, we get
f'(x) = a cos x – b (- sin x)
∴ f'(x) = a cos x + b sin x

Now, f(x) = a sin x – b cos x
∴ f(x) = (√3 + 1) sin x + (√3 – 1) cos x

VI. Fill in the blanks. (Activity Problems)

Question 1.
y = e^x . tan x
Diff. w.r.t. x

Solution:

Question 2.

diff. w.r.t. x

Solution:

Question 3.
y = (3x² + 5) cos x
Diff. w.r.t. x

Solution:

Question 4.
Differentiate tan x and sec x w.r.t. x using the formulae for differentiation of and respectively.
Solution: