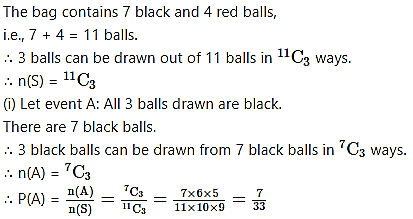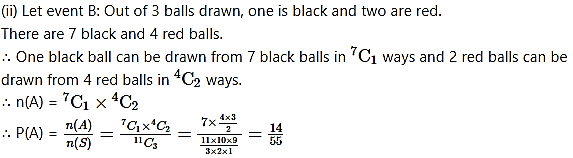Chapter 9 Probability Ex 9.1
Chapter 9 Probability Ex 9.1
Question 1.
There are four pens: Red, Green, Blue, and Purple in a desk drawer of which two pens are selected at random one after the other with replacement. State the sample space and the following events.
(a) A : Select at least one red pen.
(b) B : Two pens of the same colour are not selected.
Solution:
The drawer contains 4 pens out of which one is red (R), one is green (G), one is blue (B) and the other one is purple (P).
From this drawer, two pens are selected one after the other with replacement.
∴ The sample space S is given by
S = {RR, RG, RB, RP, GR, GG, GB, GP, BR, BG, BB, BP, PR, PG, PB, PP}
(a) A : Select at least one red pen.
At least one means one or more than one.
∴ A = {RR, RG, RB, RP, GR, BR, PR}
(b) B : Two pens of the same colour are not selected.
B = {RG, RB, RP, GR, GB, GP, BR, BG, BP, PR, PG, PB}
Question 2.
A coin and a die are tossed simultaneously. Enumerate the sample space and the following events.
(a) A : Getting a tail and an odd number.
(b) B : Getting a prime number.
(c) C : Getting head and a perfect square.
Solution:
When a coin and a die are tossed simultaneously, the sample space S is given by
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
(a) A : Getting a tail and an odd number.
∴ A = {(T, 1), (T, 3), (T, 5)}
(b) B : Getting a prime number.
∴ B = {(H, 2), (H, 3), (H, 5), (T, 2), (T, 3), (T, 5)}
(c) C : Getting a head and a perfect square.
∴ C = {(H, 1), (H, 4)}
Question 3.
Find n(S) for each of the following random experiments.
(a) From an urn containing 5 gold and 3 silver coins, 3 coins are drawn at random.
(b) 5 letters are to be placed into 5 envelopes such that no envelope is empty.
(c) 6 books of different subjects are arranged on a shelf.
(d) 3 tickets are drawn from a box containing 20 lottery tickets.
Solution:
(a) There are 5 gold and 3 silver coins, i.e., 8 coins.
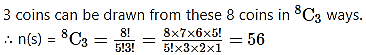
(b) 5 letters have to be placed in 5 envelopes in such a way that no envelope is empty.
∴ The first letter can be placed into 5 envelopes in 5 different ways, the second letter in 4 ways.
Similarly, the third, fourth and fifth letters can be placed in 3 ways, 2 ways and 1 way, respectively.
∴ Total number of ways = 5!
= 5 × 4 × 3 × 2 × 1
= 120
∴ n(S) = 120
(c) 6 books can be arranged on a shelf in 6P6 = 6! ways.
∴ n(S) = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
(d) 3 tickets are drawn at random from 20 tickets.
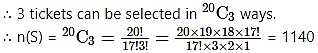
Question 4.
Two fair dice are thrown. State the sample space and write the favourable outcomes for the following events.
(a) A : Sum of numbers on two dice is divisible by 3 or 4.
(b) B : The sum of numbers on two dice is 7.
(c) C : Odd number on the first die.
(d) D : Even number on the first die.
(e) Check whether events A and B are mutually exclusive and exhaustive.
(f) Check whether events C and D are mutually exclusive and exhaustive.
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6,4), (6, 5), (6, 6)}
∴ n(S) = 36
(a) A: Sum of the numbers on two dice is divisible by 3 or 4.
∴ A = {(1, 2), (1, 3), (1, 5), (2, 1), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (3, 6), (4, 2), (4, 4), (4, 5), (5, 1), (5, 3), (5, 4), (6, 2), (6, 3), (6, 6)}
(b) B: Sum of the numbers on two dice is 7.
∴ B = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
(c) C: Odd number on the first die.
∴ C = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
(d) D: Even number on the first die.
∴ D = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
(e) A and B are mutually exclusive events as A ∩ B = Φ.
A ∪ B = {(1, 2), (1, 3), (1, 5), (1, 6), (2, 1), (2, 2), (2, 4), (2, 5), (2, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 6)} ≠ S
∴ A and B are not exhaustive events as A ∪ B ≠ S.
(f) C and D are mutually exclusive events as C ∩ D = Φ.
C ∪ D = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} = S
∴ C and D are exhaustive events.
Question 5.
A bag contains four cards marked as 5, 6, 7, and 8. Find the sample space if two cards are drawn at random
(a) with replacement.
(b) without replacement.
Solution:
The bag contains 4 cards marked 5, 6, 7, and 8. Two cards are to be drawn from this bag.
(a) If the two cards are drawn with replacement, then the sample space is
S = {(5, 5), (5, 6), (5, 7), (5, 8), (6, 5), (6, 6), (6, 7), (6, 8), (7, 5), (7, 6), (7, 7), (7, 8), (8, 5), (8, 6), (8, 7), (8, 8)}
(b) If the two cards are drawn without replacement, then the sample space is
S = {(5, 6), (5, 7), (5, 8), (6, 5), (6, 7), (6, 8), (7, 5), (7, 6), (7, 8), (8, 5), (8, 6), (8, 7)}
Question 6.
A fair die is thrown two times. Find the probability that
(a) the sum of the numbers on them is 5.
(b) the sum of the numbers on them is at least 8.
(c) the first throw gives a multiple of 2 and the second throw gives a multiple of 3.
(d) product of numbers on them is 12.
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6,4), (6, 5), (6, 6)}
∴ n(S) = 36
(a) Let event A: Sum of the numbers on uppermost face is 5.
∴ A = {(1, 4), (2, 3), (3, 2), (4, 1)}
∴ n(A) = 4
![]()
(b) Let event B: Sum of the numbers on uppermost face is at least 8 (i.e., 8 or more than 8)
∴ B = {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(B) = 15
![]()
(c) Let event C: First throw gives a multiple of 2 and second throw gives a multiple of 3.
∴ C = {(2, 3), (2, 6), (4, 3), (4, 6), (6, 3), (6, 6)}
∴ n(C) = 6
![]()
(d) Let event D: The product of the numbers on uppermost face is 12.
∴ D = {(2, 6), (3, 4), (4, 3), (6, 2)}
∴ n(D) = 4
![]()
Question 7.
Two cards are drawn from a pack of 52 cards. Find the probability that
(a) one is a face card and the other is an ace card.
(b) one is a club and the other is a diamond.
(c) both are from the same suit.
(d) both are red cards.
(e) one is a heart card and the other is a non-heart card.
Solution:
![]()
(a) Let event A: Out of the two cards drawn, one is a face card and the other is an ace card.
There are 12 face cards and 4 ace cards in a pack of 52 cards.
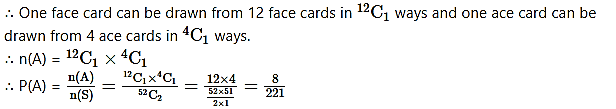
(b) Let event B: Out of the two cards drawn, one is club and the other is a diamond card.
There are 13 club cards and 13 diamond cards.

(d) Let event D: Both the cards drawn are red.

(a) Let event A: Out of the three cards drawn, 2 are queens and 1 is an ace card.
There are 4 queens and 4 aces in a pack of 52 cards.
![]()
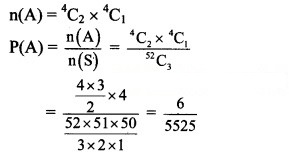
(b) Let event B: Out of the three cards drawn, at least one is a diamond.
∴ B’ is the event that all 3 cards drawn are non-diamond cards.
In a pack of 52 cards, there are 39 non-diamond cards.
![]()
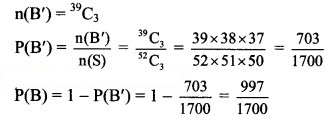
(c) Let event C: All the cards drawn are from the same suit.
A pack of 52 cards consists of 4 suits each containing 13 cards.
![]()
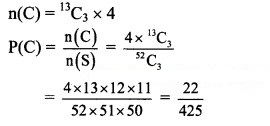
(d) Let event D: The cards drawn are a king, a queen, and a jack.
There are 4 kings, 4 queens and 4 jacks in a pack of 52 cards.


Question 9.
From a bag containing 10 red, 4 blue, and 6 black balls, a ball is drawn at random. Find the probability of drawing
(a) a red bail.
(b) a blue or black ball.
(c) not a black ball.
Solution:
The bag contains 10 red, 4 blue, and 6 black balls,
i.e., 10 + 4 + 6 = 20 balls.

(c) Let event C: Ball drawn is not black,
i.e., ball drawn is red or blue.
There are total 14 red and blue balls.
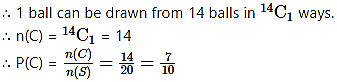
Question 10.
A box contains 75 tickets numbered 1 to 75. A ticket is drawn at random from the box. Find the probability that,
(a) number on the ticket is divisible by 6.
(b) the number on the ticket is a perfect square.
(c) the number on the ticket is prime.
(d) the number on the ticket is divisible by 3 and 5.
Solution:

Question 11.
What is the chance that a leap year, selected at random, will contain 53 Sundays?
Solution:
A leap year consists of 366 days.
It has 52 complete weeks and two more days.
These two days can be {(Sun, Mon), (Mon, Tue), (Tue, Wed), (Wed, Thur), (Thur, Fri), (Fri, Sat), (Sat, Sun)}.
∴ n(S) = 7
Let event E : There are 53 Sundays.
∴ E = {(Sun, Mon), (Sat, Sun)}
∴ n(E) = 2
![]()
Question 12.
Find the probability of getting both red balls, when from a bag containing 5 red and 4 black balls, two balls are drawn,
(i) with replacement
(ii) without replacement
Solution:
The bag contains 5 red and 4 black balls,
i.e., 5 + 4 = 9 balls.

Question 13.
A room has three sockets for lamps. From a collection of 10 bulbs of which 6 are defective. At night a person selects 3 bulbs, at random and puts them in sockets. What is the probability that
(i) room is still dark.
(ii) the room is lit.
Solution:
Total number of bulbs = 10
Number of defective bulbs = 6
∴ Number of non-defective bulbs = 4

Question 14.
Letters of the word MOTHER are arranged at random. Find the probability that in the arrangement
(a) vowels are always together.
(b) vowels are never together.
(c) O is at the beginning and end with T.
(d) starting with a vowel and ending with a consonant.
Solution:
There are 6 letters in the word MOTHER.
These letters can be arranged among themselves in 6P6 = 6! ways.
∴ n(S) = 6!
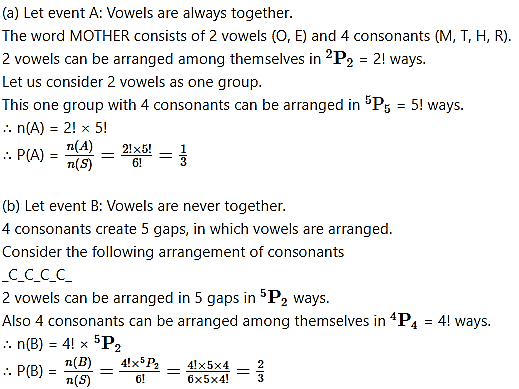

Question 15.
4 letters are to be posted in 4 post boxes. If any number of letters can be posted in any of the 4 post boxes, what is the probability that each box contains only one letter?
Solution:
There are 4 letters and 4 post boxes.
Since any number of letters can be posted in all 4 post boxes,
so each letter can be posted in different ways.
∴ n(S) = 4 × 4 × 4 × 4
Let event A: Each box contains only one letter.
∴ 1st letter can be posted in 4 different ways.
Since each box contains only one letter, 2nd letter can be posted in 3 different ways.
Similarly, 3rd and 4th letters can be posted in 2 different ways and 1 way respectively.
∴ n(A) = 4 × 3 × 2 × 1
![]()
Question 16.
15 professors have been invited for a round table conference by the Vice-chancellor of a university. What is the probability that two particular professors occupy the seats on either side of the Vice-chancellor during the conference?
Solution:
Since a Vice-chancellor invited 15 professors for a round table conference, there were all 16 persons in the conference.
These 16 persons can be arranged among themselves around a round table in (16 – 1)! = 15! ways.
∴ n(S) = 15!
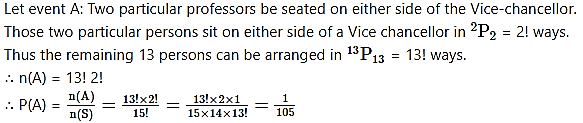
Question 17.
A bag contains 7 black and 4 red balls. If 3 balls are drawn at random, find the probability that
(i) all are black.
(ii) one is black and two are red.
Solution: