Blog

Chapter 9 Surface Area and Volume Practice Set 9.2

Chapter 9 Surface Area and Volume Practice Set 9.2

Question 1.
Perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Given: Height (h) = 12 cm, length (l) = 13 cm
To find: Radius of the base of the cone (r)
Solution:
l² = r² + h²
∴ 13² = r² + 12²
∴ 169 = r² + 144
∴169 – 144 = r²
∴ r² = 25
∴ r = √25 … [Taking square root on both sides]
= 5 cm
∴ The radius of base of the cone is 5 cm.

Question 2.
Find the volume of a cone, if its total surface area is 7128 sq.cm and radius of base is 28 cm. ( π =22/7)
Given: Radius (r) = 28 cm,
Total surface area of cone = 7128 sq.cm
To find: Volume of the cone
Solution:
i. Total surface area of cone = πr (l + r)
∴ 7128= y x 28 x (l + 28)
∴ 7128 = 22 x 4 x(l +28)

∴ l + 28 = 81
∴ l = 81 – 28
∴ l = 53cm

ii. Now, l² = r² + h²
∴ 53² = 28²+ h²
∴ 2809 = 784 + h²
∴ 2809 – 784 = h²
∴ h² = 2025

= 45 cm

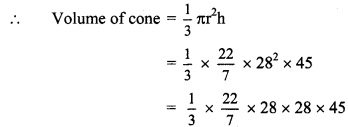
= 22 x 4 x 28 x 15
= 36960 cubic.cm
∴ The volume of the cone is 36960 cubic.cm.

Question 3.
Curved surface area of a cone is 251.2 cm² and radius of its base is 8 cm. Find its slant height and perpendicular height, (π = 3.14)
Given: Radius (r) = 8 cm, curved surface area
of cone = 251.2 cm²
To find: Slant height (l) and the perpendicular height (h) of the cone
Solution:
i. Curved surface area of cone = πrl
∴ 251.2 = 3.14 x 8 x l

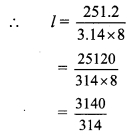
∴ l= 10 cm

ii. Now, l² = r² + h²
∴ 10² = 8² + h²
∴ 100 = 64 + h²
∴ 100 – 64 = h²
∴ h² = 36
∴ h = √36 … [Taking square root on both sides]
= 6 cm
∴ The slant height and the perpendicular height of the cone are 10 cm and 6 cm respectively.

Question 4.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is ₹ 10 per sq.m?
Given: Radius (r) = 6 m, length (l) = 8 m
To find: Total cost of making the cone
Solution:
i. To find the total cost of making the cone of tin sheet, first we need to find the total surface area of the cone.
Total surface area of the cone = πr (l + r)

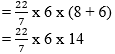
= 22 x 6 x 2 = 264 sq.m

ii. Rate of making the cone = ₹ 10 per sq.m
∴ Total cost = Total surface area x Rate of making the cone
= 264 x 10
= ₹ 2640
∴ A The total cost of making the cone of tin sheet is ₹ 2640.

Question 5.
Volume of a cone is 6280 cubic cm and base radius of the cone is 20 cm. Find its perpendicular height, (π = 3.14)
Given: Radius (r) = 20 cm,
Volume of cone = 6280 cubic cm
To find: Perpendicular height (h) of the cone
Solution:

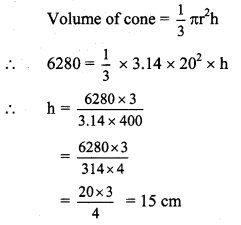
∴ The perpendicular height of the cone is 15 cm.

Question 6.
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height (π = 3.14).
Given: Length (l) =10 cm, curved surface area of the cone = 188.4 sq.cm
To find: Perpendicular height (h) of the cone
Solution:
i. Curved surface area of the cone = πrl
∴ 188.4 = 3.14 x r x 10

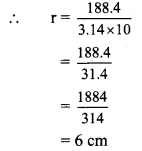
ii. Now, l² = r² + h²
∴ 10² = 6² + h²
∴ 100 = 36 + h²
∴ 100 – 36 = h²
∴ h² = 64

= 8 cm
∴ The perpendicular height of the cone is 8 cm.

Question 7.
Volume of a cone is 1232 cm³ and its height is 24 cm. Find the surface area of the cone. (π =22/7)
Given: Height (h) = 24 cm,
Volume of cone = 1232 cm³
To find: Surface area of the cone
Solution:

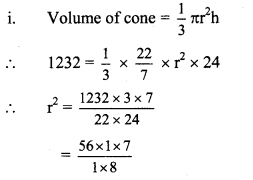
Question 8.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. (π =22/7)
Given: Length (l) = 50 cm, curved surface area of cone = 2200 sq.cm
To find: Total surface area of the cone
Solution:
i. Curved surface area of cone = πrl

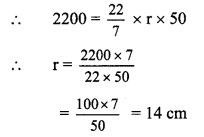
ii. Total surface area of cone = πr (l + r)


= 22 x 2 x 64
= 2816 sq.cm
∴ The total surface area of the cone is 2816 sq.cm.

Question 9.
There are 25 persons in a tent which is conical in shape. Every person needs an area of 4 sq.m, of the ground inside the tent. If height of the tent is 18 m, find the volume of the tent.
Given: For the tent,
height (h) = 18m,
number of people in the tent = 25,
area required for each person = 4 sq.m
To find: Volume of the tent
Solution:
i. Every person needs an area of 4 sq.m, of the ground inside the tent.
Surface area of the base of the tent = number of people in the tent × area required for each person
= 25 × 4
= 100 sq.m

ii. Surface area of the base of the tent = πr²
∴ 100 = πr²
∴ πr² = 100

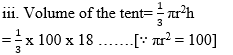
= 100 x 6
= 600 cubic metre
∴ The volume of the tent is 600 cubic metre.

Question 10.
In a field, dry fodder for the cattle is heaped in a conical shape. The height of the cone is 2.1 m and diameter of base is 7.2 m. Find the volume of the heap of the fodder. If it is to be covered by polythene in rainy se&son then how much minimum polythene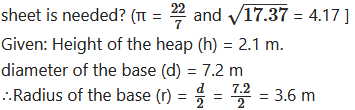

To find: Volume of the heap of the fodder and polythene sheet required
Solution:

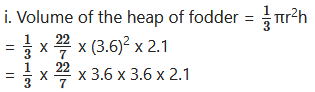
= 1 x 22 x 1.2 x 3.6 x 0.3
= 28.51 cubic metre

ii. Now, l² = r² + h²
= (3.6)² + (2.1)²
= 12.96 + 4.41
∴ l² =17.37

= 4.17 m

iii. Area of the polythene sheet needed to cover the heap of the fodder = Curved surface area of the conical heap
= πrl

= 47.18 sq.m
∴ The volume of the heap of the fodder is 28.51 cubic metre and a polythene sheet of 47.18 sq.m will be required to cover it.