Day

Night

Chp 1 solid state board exam questions

2019-2023 HSC Board Exam Paper Questions and Answer

Multiple Choice Otestions:

In body centred cubic structure, the space occupied is about
(A)
(B)
(C) .
(D)

[Mar 13]

To prepare n-type semiconductor, the impurity to be added to silicon should have the following number of valence electrons:

[Mar 14]
(A) 2
(B) 3
(C) 4
(D) 5

The major binding force in diamond is

(A) covalent bond

[Oct 14]

(B) ionic bond

(D) coordinate covalent bond

p-type semi-conductors, are made by mixing silicon with impurities of

[Mar 15]
(A) germanium
(B) boron
(C) arsenic
(D) antimony

An ionic compound crystallises in FCC type structure with ‘ ‘ ions at the centre of each face and ‘ ‘ ions occupying corners of the cube. The formula of compound is

[Mar 17]
(A)

(B)

(C)

(D)

Number of types of orthorhombic-unit cell is
(A) 7
(B) 3
(C) 4
(D) 2
The number of atoms per unit cell of body centred cube is:

[Mar 20]
(A) 1
(B) 2
(C) 4
(D) 6

The co-ordination number of atoms in body centred cubic structure (bcc) is

[Mar 22]
(A) 4
(B) 6
(C) 8
(D) 12

The CORRECT relation between edge length and radius of an atom in simple cubic lattice is

[July 22]
(A)
(B)
(C)
(D)

The relation between radius of sphere and edge length in body centered cubic lattice is given by formula:

[Mar 23]
(A)
(B)
(C)
(D)

Answers:

1.	(D)	2.	(D)	3.	(A)	4.	(B)
5.	(B)	6.	(C)	7.	(B)	8.	(C)
9.	(C)	10.	(C)

Solution:

‘As ‘ ‘ ions are present at the face centres of the 6 faces of the cube, the number of ions of ‘ ‘ in the unit cell

As ‘ ‘ is present at the 8 corners of the cube, number of ions of in the unit cell

Ratio of atoms .

The formula of the compound is .

Theur Orestions

1.2 Types of solids

Distinguish between crystalline solids and amorphous solids.

[Mar 13, 14, 17, 19]

Ans:

Crystalline solids
The constituent
particles are arranged
in a regular and
periodic manner.

The constituent particles
are arranged randomly.

ii.

They have sharp and
characteristic
melting point.

They do not have sharp
melting point. They
gradually soften over a
range of temperature.

iii.

They are anisotropic,
i.e., have different
physical properties in
different direction.

They are isotropic, i.e.,
have same physical
properties in all
directions.

iv.

They have long
range order.

They have only short
range order.

e.g.

Ice, NaCl, etc.

Glass, rubber, plastics, etc.

1.3 Classification of crystalline solids

Classify the following molecular solids into
different types:

i.	ii. ‘
iii. Solid ice	iv:

[July 18]

Ans:

i. – Polar molecular solid

ii. – Non-polar molecular solid

iii. Solid ice – Hydrogen bonded molecular solid

iv. – Polar molecular solid

Classify the following solids into different types:

i. Silver

iii. Diamond

ii.

iv.

Ans:

i. Silver-Metallic solid

ii. – Molecular solid

iii. Diamond – Covalent network solid

iv. – Ionic solid

1.5 Cubic system

A face centred cube (fcc) consists of how many atoms? Explain.

[July 16] OR

[Mar 20]

Calculate the number of atoms in a unit cell of a metal crystallising in face centred cubic structure.

[July 17]

Ans:

i. A face-centred cubic (fcc) unit cell has particles (atoms)’ at the eight corners plus particles (atoms) at the centre of its six faces.

ii. Each particle present at the corner of a given unit cell is shared with seven other neighbouring unit cells. As a result, its contribution to the given unit cell is only .

Thus, the number of atoms present at corners per unit cell corner atoms atom per unit – cell

iii. Each particle at the centre of the six faces is shared with one neighbouring cube. Thus, of each face particle belongs to the given unit cell.

Thus, the number of atoms present at faces per unit cell atoms at the faces atom per unit cell

Therefore, the total number of atoms per unit cell

Thus, fcc unit cell has total of 4 atoms per unit cell.

1.6 Packing of particles in crystal lattice

What is the ratio of octahedral holes to the number of anions in hexagonal closed packed structure?

[Mar 19]

Ans: The ratio of octahedral holes to the number of anions in hexagonal closed packed structure is .

1.7 Packing efficiency

Calculate the percentage efficiency of packing in case of simple cubic cell. [Mar 17]

Ans: Packing efficiency of metal crystal in simple cubic lattice:

Step 1: Radius of sphere:

In simple cubic unit cell, particles (spheres) are at the corners and touch each other along the edge.
Thus, or

where, ‘ ‘ is the radius of atom and ‘ ‘ is the length of unit cell edge.

Step 2: Volume of sphere:

Volume of a sphere .

Substitution for from equation (1) gives:

Volume of one particle

Step 3: Total volume of particles:

Because simple cubic unit cell contains only one particle, volume occupied by particle in unit cell

Step 4: Packing efficiency:

Packing efficiency

Thus, in simple cubic lattice, of total space is occupied by particles.

Give the relation between radius of atom and edge length in body centered cubic crystal.

[July 19]

Ans: The relation between radius of atom and edge length in body centered cubic crystal is:

1.8 Crystal defects or imperfections

What are Schottky defect and Frenkel defect?

[Oct 13]

Ans:

i. Schottky defect:

a. Schottky defect is formed in an ionic solid, when equal number of cations and anions are missing from their regular positions in the crystal lattice thereby creating vacancies. Such a paired cationanion vacancy defect is a Schottky defect.

b. This defect is found in ionic crystals such as and .

ii. Frenkel defect:

a. Frenkel defect arises when an ion of an ionic compound is missing from its regular lattice site and occupies interstitial position between lattice points. The cations are usually smaller than anions. Therefore, the cations occupy interstitial sites. Frenkel defect can be regarded as the combination of vacancy defect and interstitial defect.

b. This defect is found in ionic crystals like , and .

Explain impurity defect in stainless steel with diagram.

[Mar 15]

Ans: In interstitial impurity defect, the impurity atoms occupy interstitial spaces of lattice structure.

e.g.: Stainless steel

In stainless steel, atoms occupy normal lattice sites. The carbon atoms are present at interstitial spaces, as shown in the figure.

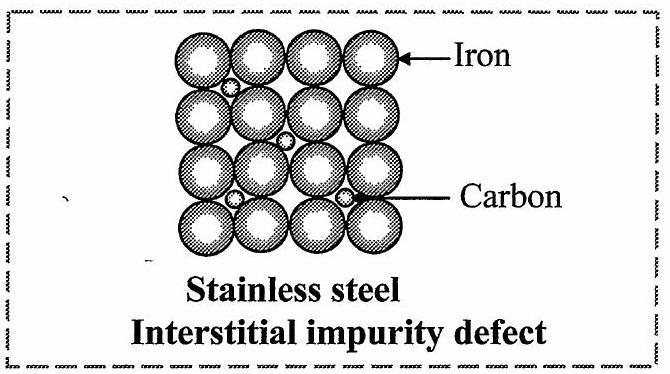
What is Schottky defect?

Ans: Refer Subtopic 1.8: Q.No.1.(i)

[July 19]

Write the consequences of Schottky defect with reasons.

[Mar 22]

Ans: Consequences of Schottky defect:

i. As the number of ions decreases, mass decreases. However, volume remains unchanged. Hence, the density of a substance decreases.

ii. The number of missing cations and anions is equal. Hence, the electrical neutrality of the compound is preserved.

Explain metal deficiency defect with example.

[Mar 22]

Ans: Metal deficiency defect:

i. This defect is possible only in compounds of metals that show variable oxidation states.

ii. In some crystals, positive metal ions are missing from their original lattice sites. The extra negative charge is balanced by the presence of cation of the same metal with higher oxidation state than that of missing cation.

e.g. In the compound , one ion is missing creating a vacancy at its lattice site. The deficiency of two positive charges is made up by the presence of two ions at the other lattice sites of ions. The composition of then becomes .

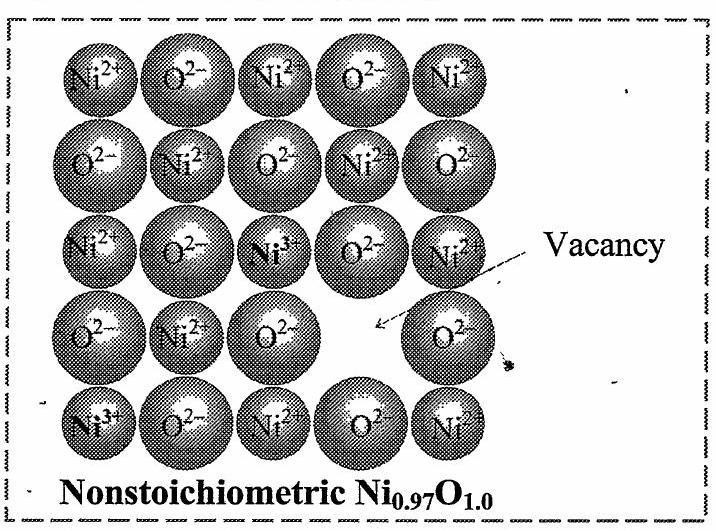
Distinguish between Schottky and Frenkel defect.

[July 22]

Ans: Differences between Schottky and Frenkel defect:

No.

Schottky defect

Frenkel defect

Schottky defect is
formed in an ionic
compound, when
equal number of
cations and anions are
missing from their
regular positions in the
crystal lattice thereby
creating vacancies. “

Frenkel defect arises
when an ion (usually
cation) of an ionic
compound is missing
from its regular
lattice site and
occupies interstitial
position between
lattice points.

ii.

Schottky defect can
be regarded as a
paired cation-anion
vacancy defect.

Frenkel defect can be
regarded as the
combination of
vacancy defect and
interstitial defect.

iii.

Schottky defect occurs
in ionic compounds
with small difference
between sizes of
cation and anion.

Frenkel defect occurs
in ionic compounds
with large difference
between sizes of
cation and anion.

iv.

Schottky defect
occurs in ionic
compounds with high
coordination number
of anion.

Frenkel defect occurs
in ionic compounds
with low coordination
number of ions.

In Schottky defect,
the density of solid
decreases.

In Frenkel defect, the
density of solid
remains unchanged.

vi.

Schottky defect is
found in ionic
crystals such as
and .

Frenkel defect is
found in ionic crystals
like ,
and .

(Any four distinguishing points)

Explain the following terms:

[Mar 23]

i. Substitutional impurity defect

ii. Interstitial impurity defect

Ans:

i. Substitutional impurity defect:

In this defect, the foreign atoms are found at the lattice sites in place of host atoms. The regular atoms are displaced from their lattice sites by impurity atoms.

e.g.: Brass :.:

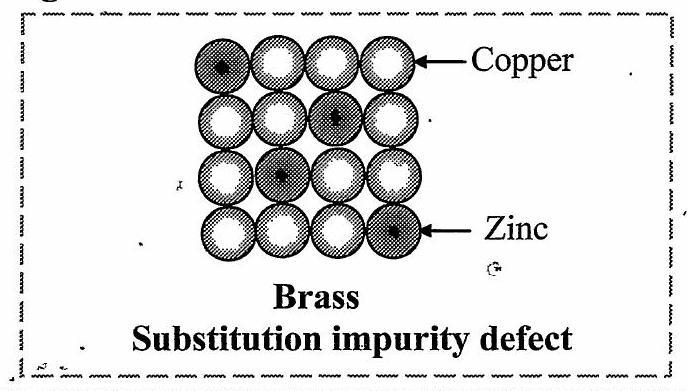
Std. XII Sci: Board Questions with Solutions (Chemistry)

ii. Interstitial impurity defect:

In this defect, the impurity atoms occupy interstitial spaces of lattice structure.

e.g.: Steel

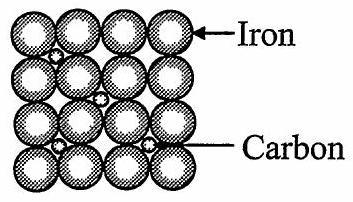
Stainless steel

Interstitial impurity defect

1.10 Magnetic properties of solids

What is ferromagnetism?

[Mar 16]

Ans: The substances containing large number of unpaired electrons-are attracted strongly by magnetic field. Such substances are called as ferromagnetic substances. The property thus exhibited is called ferromagnetism.

Numerical

1.5 Cubic system

Face centred cubic crystal lattice of copper has density of . Calculate the volume of the unit cell. Solution:

[Given: Molar mass of copper is and Avogadro number is .] [Mar 14]

Given: Density , Molar mass of copper

To find: Volume of the unit cell

Formula: Density

Calculation: For fcc unit cell, .

From formula,

Volume of unit cell,

Ans: The volume of the unit cell is .

A unit cell of iron crystal has edge length and density . Find the number of atoms per unit cell and type of the crystal lattice.

[Given: Molar mass of iron ,

Avogadro’s number ]

[Oct 14]

Solution:

Given: Edge length (a) , Atomic mass , Density

To find: Type of crystal lattice

Formula: Density

Calculation: From formula, Density,

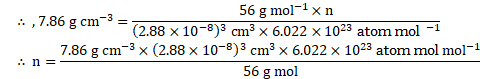
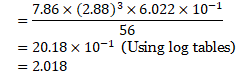
Number of atoms in unit cell

Since unit cell contains 2 atoms, it has body-centred cubic (bcc) structure.

Ans: The type of crystal lattice is body-centred cubic (bcc) lattice.

Silver crystallises in fcc (face-centred cubic crystal) structure. The edge length of the unit cell is found to be . Calculate density of the unit cell. [Given: Molar mass of silver is ] [Oct 15]

Solution:

Given:

To find:

Edge length (a) , Molar mass

Density

Formula:

Calculation: For an fcc lattice, number of atoms per unit cell is 4.

From formula, Density,

Ans: Density of silver is .

Silver crystallises in fec structure. If density of silver is , calculate the volume of unit cell.

[Mar 16]

Solution:

Given: Density

To find: Volume of the unit cell

Formula:

Density

Calculation: For fcc unit cell, .

From formula, Volume of unit cell,

Ans: The volume of the unit cell is .

Determine the density of cesium chloride which crystallizes in bec type structure with the edge length . The atomic masses of and are 133 and 35.5 respectively.

Solution:

Given: Edge length (a) , Molar mass

To find: Density

Formulae: i. Mass of one molecule

ii. Volume of unit cell

iii. Density

Calculation: In the bcc type unit cell of , there is one ion at the body centre position and ions are at the 8 corners.

Number of in unit cell

Hence, the unit cell contains one molecule.

Std. XII Sci. Board Questions with Solutions (Chemistry)

Mass of one molecule

Mass of unit cell

Volume of unit cell

Density

Ans: Density of cesium chloride is .

A metal crystallises into two cubic faces namely face centred (fcc) and body centred (bcc), whose unit cell edge lengths are 3.5 and 3.0 respectively. Find the ratio of the densities of fec and bcc. [July 17]

Solution:

Given: Edge length of fcc unit cell Edge length of bcc unit cell

To find: Ratio of densities of fcc and

Formula: Density of unit cell

Calculation: -For fcc unit cell, .

Density of fcc unit cell

For bcc unit cell, .

Density of bcc unit cell ,

Ratio of densities of fcc and bcc unit cell is,

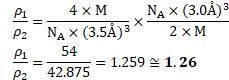
Ans: The ratio of densities of fcc and bcc structures is

The density of iron crystal is . If the edge length of unit cell is and atomic mass is , find the number of atoms in the unit cell.

[Given: Avogadro’s number ]

Solution:

Given: Edge length (a) , Atomic mass , Density

To find: Number of atoms in the unit cell

Formula: Density

Calculation: From formula,

Density,

Number of atoms in unit cell

Ans: The number of atoms in the unit cell is 2.

The density of silver having atomic mass is . If the edge, length of cubic unit cell is , find the number of silver atoms in the unit cell.

[July 18]

Solution:

Given: Édge length (a) , Atomic mass , Density

To find: Number of silver atoms in the unit cell

Formula: Density

Calculation: From formula,

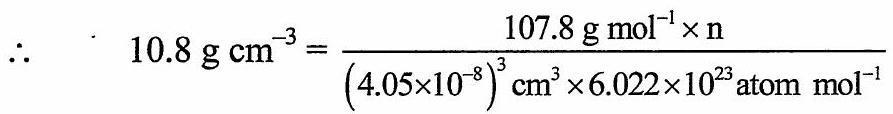
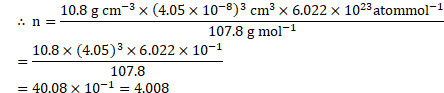
Number of silver atoms in unit cell

Ans: The number of silver atoms in the unit cell is 4 .

Unit cell of a metal has edge length of and density of . Determine the type of crystal lattice. [Atomic mass of metal ]

[Mar 20]

Solution: Refer Subtopic 1.5: Numerical Q. No. 2.

Gold crystallises into face-centred cubic cells. The edge length of unit cell is . Calculate the density of gold. [Molar mass of gold ]

Solution:

Given:

To find: Density

Formula: Density

Calculation: For an fcc lattice, number of atoms per unit cell is 4 .

From formula,

Density,

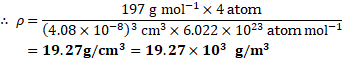
Ans: Density of gold is .

Silver crystallizes in fce structure. If edge length of unit cell is , calculate density of silver (Atomic mass of ).

Solution:

Given:

Edge length (a)

To find:

Atomic mass of

Formula:

Density

Std. XII Sci: Board Questions with Solutions

Calculation: . For an fcc lattice, number of atoms per unit cell is 4.

Ans: Density of silver is .

1.7. Packing efficiency

Gold occurs as face centred cube and has a density of . Calculate atomic radius of gold. [Molar mass of

Solution:

Given: Type of unit cell is fcc.

Density of gold

Molar mass of gold

To find: Radius of gold atom

Formulae: i. Density ii. For fcc unit cell,

Calculation: For fcc unit cell, .

Using formula (i),

Density

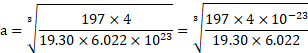
Using formula (ii),

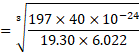
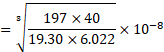
Ans: Radius of gold atom ( ) is .

Niobium crystallises as body centred cube (bcc) and has density of . Calculate the atomic radius of niobium.’

[Given: Atomic mass of niobium =93]

[Mar 15]

Solution:

Given: Type of unit cell is bcc.

Density of niobium

Molar mass of niobium

To find: Radius of niobium atom ( )

Formulae: i. Density

ii. For bcc unit cell,

Calculation: For bcc unit cell, .

Using formula (i),

Density

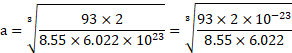
Using formula (ii),

Ans: Radius of niobium atom ( ) is .

Calculate the number of atoms and unit cells present in of Niobium if it forms body centred cubic structure. The density of Niobium is and edge length of unit cell is .