HSC PHQ 01 Rotational Dynamics – Maharashtra Board Solutions

01 Rotational Dynamics

Multiple Choice Questions

1. A car is moving along a horizontal curve of radius

and coefficient of friction between the road and wheels of the car is 0.25 . If acceleration due to gravity is

, then its maximum speed is

(A)
(B)
(C)
(D)

Ans. (C)

2. A body is acted upon by a constant torque. In 4 seconds its angular momentum changes from to . The magnitude of the torque is ………………………

(A)
(B)
(C)
(D)

Ans. (B)

3. Radius of gyration of a ring about a transverse axis passing through its centre is ………………………

(A) diameter of ring

(B) diameter of ring

(D) (diameter of ring)

Ans. (A) diameter of ring

4. A stone is tied to a string and rotated in a horizontal circle with constant angular velocity. If the string is released, the stone flies ………………………

(A) radially inward

(B) radially outward

(D) tangentially backward

Ans. (C) tangentially forward

5. The radius of gyration of a solid sphere of mass and radius rotating about an axis with its diameter is

(A)
(B)
(C)
(D)

Ans. (B)

6. The moment of inertia of a thin uniform rod of mass and length , about an axis passing through a point, midway between the centre and one end, perpendicular to its length is [Mar 13]

(A)
(B)
(C)
(D)

Ans. (B)

7. If ‘ ‘ is the angular momentum and ‘ ‘ is the moment of inertia of a rotating body, then represents its

(A) rotational P.E.
(B) total energy
(C) rotational K.E.
(D) translational K.E.

Ans. (C) rotational K.E.

8. A thin wire of length and uniform linear mass density is bent into a circular coil. Moment of inertia of the coil about tangential axis in its plane is ………………………

(A)
(B)
(C)
(D)

Ans. (C)

9. The period of a conical pendulum in terms of its length , semivertical angle and acceleration due to gravity is:
(A)
(B)
(C)
(D)

Ans. (C)

10. The kinetic energy of a rotating body depends upon

(A) distribution of mass only.

(B) angular speed only.

(D) angular acceleration only.

Ans. (C) distribution of mass and angular speed.

11. A particle rotates in U.C.M. with tangential velocity ‘ ‘ along a horizontal circle of diameter ‘ ‘. Total angular displacement of the particle in time ‘ ‘ is ………………………

(A)
(B)

(D)

Ans. (D)

12. A body of moment of inertia rotating with an angular velocity has the same kinetic energy as a mass of moving with a velocity of ………………………

(A)
(B)
(C)
(D)

Ans. (C)

13. The difference in tensions in the string at lowest and highest points in the path of the particle of mass ‘ ‘ performing vertical circular motion is

(A)
(B)

Ans. (C)

14. The body is rotating with uniform angular velocity having rotational kinetic energy (E). Its angular momentum (L) is: [July 16]

(A)
(B)
(C)
(D)

Ans. (A)

15. When the angular acceleration of a rotating body is zero, which physical quantity will be equal to zero?

(A) Angular momentum

(B) Moment of inertia

(D) Radius of gyration

Ans. (C) Torque

16. A body of mass ‘ ‘ performs uniform circular motion along a circular path of radius ‘ ‘ with velocity ‘ ‘. If its angular momentum is , then the centripetal force acting on it is ………………………

(A)
(B)
(C)
(D)

Ans. (D)

17. If a rigid body of radius ‘ ‘ starts from rest and rolls down an inclined plane of inclination ‘ ‘ then linear acceleration of body rolling down the plane is ………………………

(A)
(B)
(C)
(D)

Ans. (C)

18. A particle of mass performs vertical motion in a circle of radius . Its potential energy at the highest point is ………………………

( is acceleration due to gravity)

(A)
(B)
(C) 0
(D)

Ans. (A)

19. A thin ring has mass and radius . Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………………………

(A)
(B)

Ans. (A)

20. The dimensions of angular momentum are ………………………

(A)
(B)

Ans. (B)

21. In rotational motion of a rigid body, all particles move with ………………………

(A) same linear velocity and same angular velocity

(B) same linear velocity and different angular velocity

(D) different linear velocities and different angular velocities

Ans. (C) different linear velocities and same angular velocities

22. When the bob performs a vertical circular motion and the string rotates in a vertical plane, the difference in the tension in the string at horizontal position and uppermost position is ………………………

(B)
(C)
(D)

Ans. (C)

Theory Questions

Characteristics of Circular Motion

1. Explain the concept of centripetal force.

Ans: Centripetal force:

i. The force providing centripetal or radial acceleration is called as centripetal or radial force.

where, radius of circular path.

ii. In magnitude,

iii. The direction of this force is along the radius and towards centre (centre seeking).

2. Distinguish between centripetal force and centrifugal force.

Ans:

	Centripetal Force	Contrinugen force
i.	Centripetal force isdirected along theradius towards thecentre of a circle.	Centrifugal force isdirected along theradius away fromthe centre of acircle.
ii.	It is a real force.	It is a pseudo force.
iii.	It is considered ininertial frame ofreference.	It is considered innon-inertial frame ofreference.
iv.	In vector form, it isgiven bywith usual notations.	In vector form, it isgiven bywith usual notations.

3. What is the value of tangential acceleration in U.C.M.?

Ans: Value of tangential acceleration in U.C.M. is always zero.

4. Define U.C.M.

Name the forces acting on a body executing nonuniform circular motion.

Ans: Definition: During circular motion, if the speed of the particle remains constant, it is called Uniform Circular Motion (UCM).

Forces acting on the body executing nonuniform circular motion: Centripetal force provided partly by the weight of the body performing circular motion and partly by the normal reaction.

5. Define uniform circular motion.

Ans: Refer Subtopic 1.2: Q. No. 4 (Definition only)

Applications of Uniform Circular Motion

1. Derive an expression for period of a conical pendulum.

Ans:

i. Consider the vertical section of a conical pendulum having bob (point mass) of mass and string of length ‘ ‘.

ii. Here, is the angle made by the string with the vertical, at any position (semi-vertical angle of the cone)

iii. In a given position , the forces acting on the bob are

a. its weight ‘ ‘ directed vertically downwards

b. the force ‘ ‘ due to the tension in the string, directed along the string, towards the support .

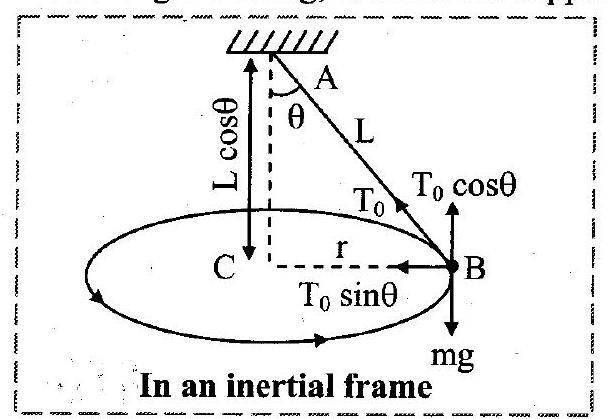
iv. As the motion of the bob is a horizontal circular motion, the resultant force must be horizontal and directed towards the centre of the circular motion.

v. For this, tension in the string is resolved into

a. : vertical component

b. : horizontal component

vi. The vertical component balances the weight ‘ ‘.

vii. The horizontal component then becomes the resultant force which is centripetal.

Dividing equation (2) by equation (1),

viii. From the figure,

From equation (3) and (4),

ix. If is the period of revolution of the bob, then

Period,

2. For a conical pendulum prove that

Ans:

i. Consider bob of mass tied to one end of a string of length ‘ ‘ and other end is fixed to rigid support.

ii. Let the bob be displaced from its mean position and whirled around a horizontal circle of radius ‘ ‘ with constant angular velocity , then the bob performs U.C.M.

iii. During the motion, string is inclined to the vertical at an angle as shown in the figure.

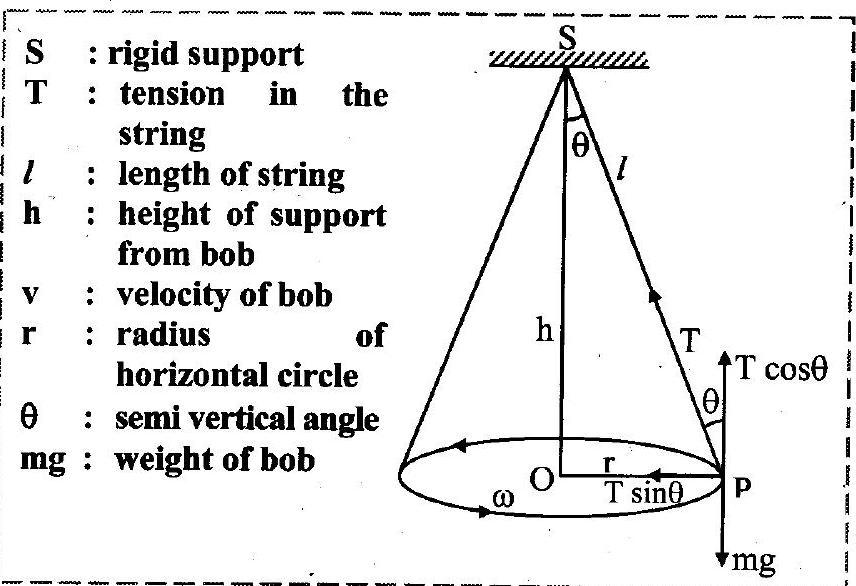
iv. In the displaced position , there are two forces acting on the bob.

a. The weight acting vertically downwards.

b. The tension T acting upward along the string.

v. The tension (T) acting in the string can be resolved into two components:

a. acting vertically upwards.

b. acting horizontally towards centre of the circle.

vi. Vertical component balances the weight and horizontal component provides the necessary centripetal force.

vii. Dividing equation (2) by (1), we get

3. Obtain an expression for maximum speed with which a vehicle can be driven safely on a banked road. Show that the safety speed limit is independent of the mass of the vehicle.

Ans:

i. The vertical section of a vehicle on a curved road of radius ‘ ‘ banked at an angle ‘ ‘ with the horizontal is shown in the figure.

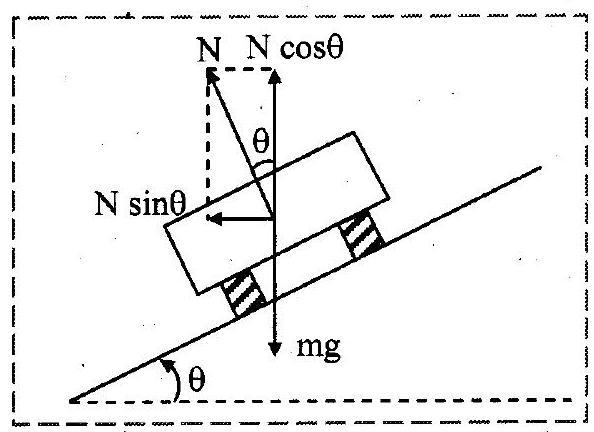
ii. Considering the vehicle to be a point and ignoring friction (not eliminating) and other non-conservative forces like air resistance, there are two forces acting on the vehicle:

a. weight , vertically downwards

b. normal reaction , perpendicular to the surface of the road.

iii. As the motion of the vehicle is along a horizontal circle, the resultant force must be horizontal and directed towards the centre of the track. Hence, the vertical force must be balanced.

iv. Thus, normal reaction is resolved into,

a. – along the horizontal.

b. – along the vertical.

v. The vertical component balances the weight,

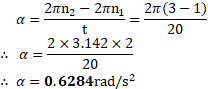
vi. Horizontal component being the resultant force, must be the necessary centripetal force (or balance the centrifugal force).

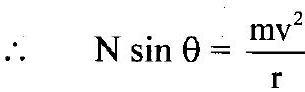
Dividing equation (2) by equation (1),

vii. Thus, most safe speed,

viii. As the equation doesnot contain mass , it is independent of mass of the vehicle.

4. Draw a diagram showing all components of forces acting on a vehicle moving on a curved banked road. Write the necessary equation for maximum safety speed and state the significance of each term involved in it.

Ans:

Equation for maximum safety speed:

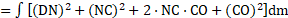
where, radius of curved road,

angle of banking

coefficient of friction

acceleration due to gravity

5. Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length. [Oct 15]

Ans:

Expression for its periodic time in terms of length:

6. Draw a neat labelled diagram showing the various forces and their components acting on a vehicle moving along curved banked road.

Ans: Refer Subtopic 1.3: Q. No. 4.

7. Draw neat, labelled diagram showing different forces acting on a vehicle moving along a banked road.

Ans: Refer Subtopic 1.3: Q. No. 4.

8. If friction is made zero for a road, can a vehicle move safely on this road?

Ans: No, vehicle will skid in the absence of friction on the road.

Vertical Circular Motion

1. A particle of mass , just completes the vertical circular motion. Derive the expression for the difference in tensions at the highest and the lowest points. [Mar 13]

Ans:

i. Consider a particle of mass moving along a vertical circle.

ii. At any position of the particle, there are only two forces acting on the particle:

a. weight (mg), vertically downwards, which is constant

b. the force due to the tension (T), directed towards the centre. (Its magnitude changes periodically with time and location.)

iii. As the motion is non uniform, the resultant of these two forces is not directed towards the centre except at the uppermost and the lowermost positions of the bob.

iv. Uppermost position (A):

a. Both, weight and force due to tension are downwards, i.e., towards the centre. In this case, their resultant is used only as the centripetal force.

b. Thus, if is the speed at the uppermost point,

c. For minimum possible speed at this point (or if the motion is to be realized with minimum possible energy),

v. Lowermost position (B):

a. Force due to the tension, is vertically upwards, i.e., towards the centre, and opposite to . In this case, their resultant is the centripetal force.
b. If is the speed at the lowermost point,

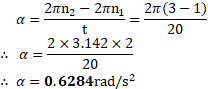
c. While coming down from the uppermost to the lowermost point, the vertical displacement is and the motion is governed only by gravity.

d. Hence the corresponding decrease in the gravitational potential energy is converted into the kinetic energy.

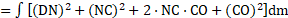
vi. Difference between the extreme tensions: Subtracting equation (1) from equation (3),

Using equation (4) and rearranging, we get,

Hence, difference in tension at extreme positions depends only on weight.

2. Derive expressions for linear velocity at lowest position, mid-way position and the top-most position for a particle revolving in a vertical circle, if it has to just complete circular motion without string slackening at top.

Ans: Refer Subtopic 1.4: Q. No. I(i) to (v) and diagram

vi. Positions when the string is horizontal (C. and D):

a. Force due to the tension is the only force towards the centre as weight is perpendicular to the tension.

b. Thus, force due to the tension is the centripetal force used to change the direction of the velocity and weight is used only to change the speed.

c. At midway position (C), while coming down from the midway point to the lowermost point, the vertical displacement is ‘ ‘.

Hence, the corresponding decrease in the gravitational P.E. is converted into K.E.

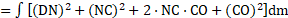
Since,

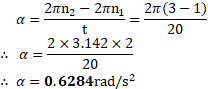
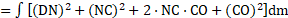
Similarly

Moment of Inertia as an Analogous Quantity for Mass

1. Define moment of inertia of a rotating rigid body. State its SI unit and dimensions.

Define moment of inertia. State its SI unit and dimensions. [Oct 08, Mar 18]
Ans: Definition: Moment of inertia of a rigid body about an axis of rotation is defined as the sum of product of the mass of each particle and the square of its perpendicular distance from the axis of rotation.

i. SI unit of moment of inertia is .

ii. Dimensions are .

2. Derive an expression for kinetic energy of a rotating body.

Derive an expression for the kinetic energy of a body rotating with a uniform angular speed.

Ans: Derivation of an expression for the kinetic energy of a body rotating with a uniform angular speed:

i. Consider a rigid object rotating with a constant angular speed about an axis perpendicular to the plane of paper.

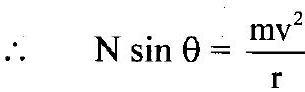
ii. For theoretical simplification, let us consider the object to be consisting of particles of masses at respective perpendicular distances from the axis of rotation.

iii. As the object rotates, all these particles perform UCM with the same angular speed , but with different linear speeds,

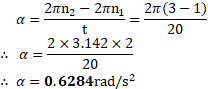
iv. Translational K.E. of the first particle is, (K.E.

Translational K.E. of the second particle is, (K.E.)

Similar will be the case of all the remaining particles.

v. Rotational K.E. of the object is the sum of individual translational kinetic energies. Thus,

Rotational K.E.

But

Rotational K.E.

Radius of Gyration

1. Explain the physical significance of radius of gyration.

Ans:

i. Calculation of moment of inertia is possible only for mathematically integrable geometrical shapes.

ii. However, experimentally one can determine the moment of inertia of any object.

iii. It depends upon mass of that object and how that mass is distributed from or around the given axis of rotation.

iv. If one is interested in knowing only the mass distribution around the axis of rotation, we can express moment of inertia of any object as , where is mass of that object.

v. It means that the mass of that object is effectively at a distance from the given axis of rotation.

vi. In this case, is defined as the radius of gyration of the object about the given axis of rotation.

vii. In other words, if is radius of gyration for an object, is the moment of inertia of that object.

2. Define radius of gyration and give its physical significance.

Ans: Definition: Radius of gyration of a body about its given axis is defined as the distance between the axis of rotation and a point at which the whole mass of the body is supposed to be concentrated, so as to possess the same moment of inertia as that of body about the same axis.

Physical significance:

Refer Subtopic 1.6: Q. No. 1

3. Define radius of gyration. Write its physical significance.

Ans: Refer Subtopic 1.6: Q. No. 1 (Definition)

Refer Subtopic 1.6: Q. No. 2 (Physical significance)

Theorem of Parallel Axes and Theorem of Perpendicular Axes

1. State and prove the principle of perpendicular axes.

Ans: Statement:

The moment of inertia of a laminar object about an axis (Z) perpendicular to its plane is the sum of its moment of inertia about two mutually perpendicular axes ( and ) in its plane, all the three axes being concurrent.

Mathematically,

Proof:

i. Consider a rigid laminar object able to rotate about three mutually perpendicular axes and .

ii. Axes and are in the plane of the object while the axis is perpendicular to it, and all are concurrent at .

iii. Consider a mass element located at any point and are the perpendiculars drawn from respectively on the and axes.

iv. The respective perpendicular distances of point from and axes will then be and .

v. If and are the respective moment of inertia of the body about and axes, then , ,

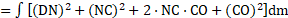
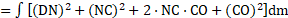
This is the mathematical form of the theorem of perpendicular axes.

2. State and prove theorem of parallel axes.

Ans: Statement: The moment of inertia of an object about any axis is the sum of its moment of inertia ) about an axis parallel to the given axis, and passing through the centre of mass and the product of the mass of the object and the square of the distance between the two axes.

Mathematically,

Proof:

i. Consider an object of mass M. Axis MOP is any axis passing through point .

ii. Axis ACB is passing through the centre of mass of the object, parallel to the axis MOP, and at a distance from it .

Theorem of parallel axes

iii. Consider a mass element ‘ ‘ located at point D. Perpendicular on (produced) from point is .
iv. Moment of inertia of the object about the axis is , and about the axis MOP it is .

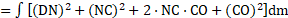
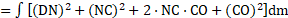
….(using Pythagoras theorem in

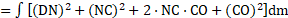
Now, and

v. is the distance of a point from the centre of mass. Any mass distribution is symmetric about the centre of mass. Thus, from the definition of the centre of mass,

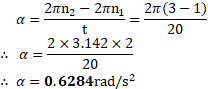
This is the mathematical form of the theorem of parallel axes.

2. State theorem of parallel axes and theorem of * perpendicular axes about moment of inertia.

Ans: Parallel axes theorem: Refer Subtopic 1.7: . No. 2 (Statement only)

Perpendicular axes theorem: The moment of inertia of a laminar object about an axis (Z) perpendicular to its plane is the sum of its moment of inertia about two mutually perpendicular axes ( and ) in its plane, all the three axes being concurrent.

Mathematically,

4. State an expression for the moment of inertia of a solid uniform disc, rotating about an axis passing through its centre, perpendicular to its plane.

Ans: Expression of M.I of uniform disc about an axis passing through its centre and perpendicular to its plane:

i. Let, mass of disc,

radius of disc

axis passing through the centre of disc and perpendicular to the plane.

ii. The M. I of a thin uniform disc about an axis passing through its centre and perpendicular to its plane is given by,

5. State and prove theorem of parallel axes about moment of inertia.

Ans: Refer Subtopic 1.7: Q. No. 2

6. State and prove the principle of parallel axes in rotational motion.

Ans: Refer Subtopic 1.7: Q. No. 2

Angular Momentum or Moment of Linear Momentum

1. Show that the kinetic energy of a rotating body about a given axis is equal to , where is angular momentum and is angular velocity.

Ans:

i. Consider a rigid object rotating with a constant angular speed about an axis perpendicular to the plane of paper.

ii. For theoretical simplification, let us consider the object to be consisting of particles of masses at respective perpendicular distances from the axis of rotation.

iii. As the object rotates, all these particles perform UCM with the same angular speed , but with different linear speeds,

iv. Translational K.E. of the first particle is

(K.E.

Similar will be the case of all the other particles.

v. Rotational. K.E. of the object, is the sum of individual translational kinetic energies.

Thus,

Rotational K.E. =

Rotational K.E.

But

Rotational K.E.

But angular momentum of rotating body is given by,

From equation (i), K.E

Substitute I from equation (ii), in equation (i), we get,

Expression for Torque in Terms of Moment of Inertia

1. Obtain an expression for torque acting on a body rotating with uniform angular acceleration.

Ans:

i. Consider a rigid object rotating with a constant angular acceleration ‘ ‘ about an axis perpendicular to the plane of paper.

ii. Let us consider the object to be consisting of number of particles of masses at respective perpendicular distances from the axis of rotation.

iii. As the object rotates, all these particles perform circular motion with same angular acceleration , but with different linear (tangential) accelerations , , etc.

iv. Force experienced by the first particle is,

v. As these forces are tangential, the irrespective perpendicular distances from the axis are ,

vi. Thus, the torque experienced by the first particle is of magnitude

Similarly,

vii. If the rotation is restricted to a single plane, directions of all these torques are the same, and along the axis.

viii. Magnitude of the resultant torque is then given by

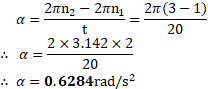
where, is the moment of inertia of the object about the given axis of rotation.

2. Obtain an expression for torque acting on a rotating body with constant angular acceleration. Hence state the dimensions and SI unit of torque.

Ans: Expression for torque acting on a rotating body: Refer Subtopic 1.9: Q. No. 1

SI unit:

Dimensions:

onservation of Angular Momentum

1. State the law of conservation of angular momentum and explain with a suitable example.

Ans:

i. Statement: Angular momentum of an isolated system is conserved in the absence of an external unbalanced torque.

ii. Illustration:

Ballet dancers:

a. During ice ballet, the dancers have to undertake rounds of smaller and larger radii.

b. The dancers come together by taking rounds of smaller radius (near the centre).

c. In this case, the moment of inertia of their system becomes minimum and the frequency increases, to make it thrilling.

d. While during outer rounds, the dancers outstretch their legs and arms.

e. This increases their moment of inertia that reduces the angular speed and hence the linear speed. This is essential to prevent slipping.

2. State and prove: law of conservation of angular momentum.

Ans: Statement: Refer Subtopic 1.10: Q. No. 1 Proof:

i. Angular momentum or the moment of linear momentum of a system is given by,

where is the position vector from the axis of rotation and is the linear momentum.

ii. Differentiating with respect to time, we get,

iii. Now, and

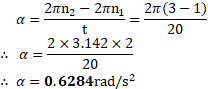
Now

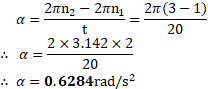
iv. But is the moment of force or torque .

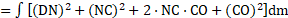
Thus, if or constant.

Hence, angular momentum is conserved in the absence of external unbalanced torque .

3. State and prove principle of conservation of angular momentum.

Ans: Statement: Refer Subtopic 1.10: Q. No. 1

Proof: Refer Subtopic 1.10: Q. No. 2

4. Explain the principle of conservation of angular momentum with the help of two appropriate examples.

Ans: Statement and explanation:

Refer Subtopic 1.10: Q. No. 1 and Q. No. 2

Examples:

i. The angular velocity of revolution of a planet around the sun in an elliptical orbit increases, when the planet comes closer to the sun and vice-versa.

ii. A person carrying heavy weights in his hands and standing on a rotating platform can change the speed of the platform.

iii. A diver performs somersaults by jumping from a high diving board keeping his legs and arms out stretched first, and then curling his body.

5. State the law of conservation of angular momentum.

Ans: Statement: Refer Subtopic 1.10: Q. No. 1

1.11 Rolling Motion

1. Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.

Ans: Expression for kinetic energy of rolling sphere:

i. Mass of the sphere is given to be .

Let, linear velocity of the sphere

angular velocity of the sphere

I = moment of inertia of the sphere

= radius of gyration

ii. Total K.E of rolling body

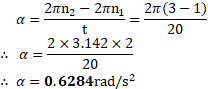
and

Since the value of ‘ ‘ is different for different bodies, so (K:E)rolling also varies from body to body.

2. Obtain an expression for total kinetic energy of a rolling body in the form .

Ans: Refer Subtopic 1.11: Q. No. 1

Numerical

Characteristics of Circular Motion

1. An object of mass attached to wire of length is revolved in a horizontal circle. If it makes 60 r.p.m. Find its

i. angular speed

ii. linear speed

iii. centripetal acceleration

iv. centripetal force

Solution:

Given: r.p.m. r.p.s.

To find:

i. Angular Speed

ii. Linear Speed (v)

iii. Centripetal acceleration

iv. Centripetal Force

Formulae: i. ii.

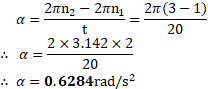
Calculation: From formula (i),

From formula (ii),

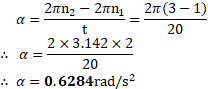
From formula (iii),

From formula (iv),

Ans: i. The angular speed id .

ii. The linear speed of an object id .

iii. The centripetal acceleration of an object is .

iv. The centripetal force is .

2. A car of mass rounds a curve of radius at hour. Calculate the centripetal force acting on it.

Solution:

Given: ,

To find: Centripetal force

Formula:

Calculation: From formula,

Ans: The centripetal force acting on the car is .

3. A racing car completes rounds of a circular track in 2 minutes. Find the radius of the track if the car has uniform centripetal acceleration of .

Solution:

Given: rounds minutes

To find: Radius (r)

Formula:

Calculation: From formula,

Ans: The radius of the track is .

4. A stone of mass is whirled in horizontal circle attached at the end of a long string. If the string makes an angle of with vertical, calculate the centripetal force acting on the stone. .

Solution:

Given:

To find:

Centripetal force

Formulae: i. ii.

Calculation: Substituting formula (ii) in (i),

Ans: The centripetal force acting on the stone is .

5. The spin dryer of a washing machine rotating at 15 r.p.s. slows down to 5 r.p.s. after making 50 revolutions. Find its angular acceleration.

Solution:

Given: r.p.s., r.p.s.,

No. of revolutions

To find: Angular acceleration

Formulae: i. ii.

Calculation: From formula (i),

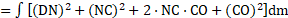
In 1 revolution,

angular displacement

in 50 revolutions,

angular displacement

Using formula (ii),

Ans: Angular acceleration of spin dryer is .

6. A coin kept at a distance of from the centre of a turntable of radius just begins to slip when the turntable rotates at a speed of 90 r.p.m. Calculate the coefficient of static friction between the coin and the turntable. .

Solution:

Given:

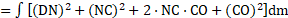
To find: Coefficient of static friction

Formula:

Calculation: Since,

Ans: The coefficient of static friction between the coin and the turntable is 0.4527 .

7. The frequency of revolution of a particle performing circular motion changes from 60 r.p.m. to 180 r.p.m. in 20 seconds. Calculate the angular acceleration of the particle.

Solution:

To find: Angular acceleration ( )

Formula:

Calculation: From formula,

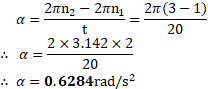
Ans: Angular acceleration of the particle is .

8. Find the frequency of revolution of a round disco stage revolving with an angular speed of .

Solution:

Let the disco stage revolves with angular speed .

Given that degree/second

Frequency of revolution

Ans: Frequency of revolution of the revolving disco stage is or .

1.3 Applications of Uniform Circular Motion

1. In a conical pendulum, a string of length is fixed at rigid support and carries a mass of at its free end. If the mass is revolved in a horizontal circle of radius around a vertical axis, calculate tension

Solution: in the string.

Given: ,

To find: Tension in the string ( )

Formula: Tension,

Calculation:

By Pythagoras theorem,

The weight of bob is balanced by vertical component of tension .

From figure,

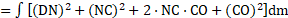
Substituting in formula,

Ans: Tension in the string is .

2. A stone of mass is whirled in a horizontal circle attached at the end of long string. If the string makes an angle of with vertical,

Solution:

compute its period.

[July 16]

Given:

To find: Period (T)

Formula:

Calculation: From formula,

Ans: Period of revolution is .

3. A vehicle is moving on a circular track whose surface is inclined towards the horizon at an angle of . The maximum velocity with which it can move safely is . Calculate the length of the circular track.

Solution:

Given: ,

To find: Length of circular track

Formula:

Calculation: From formula,

Ans: The length of the circular track is .

4. A small body of mass oscillates in vertical plane with the help of a string long with a constant speed of . It makes an angle of with the vertical. Calculate tension in the string . [July 17]

Solution:

Given:

To find: Tension (T)

Formulae:

Calculation: From formula,

Ans: The tension in the string is .

5. A flat curve on a highway has a radius of curvature . A car goes around a curve at a speed of . What is the minimum value of coefficient of friction that will prevent the car from sliding?

Solution:

Given:

To find: Coefficient of friction

Formula:

Calculation: From formula,

Ans: The value of coefficient of friction between tyre and ground is .

6. A metre-gauge train is moving at along a curved rail-way of radius of curvature at a certain place. Find the elevation of the outer rail above the inner rail so that there is no side pressure on the rail.

Solution:

Given: Radius of curve, r = 500 m,

Speed of train, v = 72km/hr

= 72 x 5/18 = 20m/s

To find: Elevation of rails

Formulae:

Calculation:

From formula (i),

From formula (ii),

Ans: The elevation of the outer rail above the inner rail is .

7. A car rounds a curve of radius with a speed of . What is the minimum value of coefficient of friction which prevents the car from sliding?

Solution:

Given:

To find: Coefficient of friction .

Formula:

Calculation: From formula,

Ans: The value of coefficient of friction between tyre and ground is .

Vertical Circular Motion

1. An object of mass is tied to one end of a string of length and whirled in a vertical circle. What is the minimum speed required at the lowest position to complete a circle?

Solution:

Given:

To find: Minimum velocity at the lowest point

Formula:

Calculation: From formula,

Ans: The minimum velocity at the lowest point is .

2. A stone of mass , tied to one end of a rope of length , is whirled in a vertical circle. Find the minimum velocity at the highest point and at the midway point.

Solution:

Given:

To find: \begin{tabular}{ll}

i. &

Minimum velocity at the highest

point

ii. &

Minimum velocity at midway

point

\end{tabular}

Formulae: i. ii.

Calculation: From formula (i),

From formula (ii),

Ans: The minimum velocity at the highest point and midway point is and respectively.

3. A stone of mass attached to a string of length is whirled in a vertical circle by giving velocity at lowest point as . Find the velocity at the highest point.

[Acceleration due to gravity ]

Solution:

Given:

To find: , Velocity at the highest point

Calculation: Total energy at highest point,

From formula,

Ans: The velocity at the highest point is .

4. In a Circus, a motor-cyclist having mass of moves in a spherical cage of radius . Calculate the least velocity with which he must pass the highest point without losing contact. Also calculate his angular speed at the highest point.

Solution:

Given:

To find: i. Velocity at highest point

ii. Angular velocity at highest point

Formulae: i. ii.

Calculation: Using formula (i),

Ans: The least velocity with which the motor cyclist must pass the highest is and the angular velocity at the highest point is .

1.5 Moment of Inertia as an Analogous Quantity for Mass

1. Energy of is spent to increase the angular speed of a wheel from to . Calculate the moment of inertia of the wheel.

Solution:

Given: r.p.s, r.p.s,
To find: Moment of inertia (I)

Formula: K.E

Calculation: From formula,

Ans: The moment of inertia of the wheel is

Theorem of Parallel Axes and Theorem of Perpendicular Axes

1. A solid cylinder of uniform density of radius has mass of . If its length is , calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.

Solution:

Given: ,

To find: Moment of inertia (I)

Formula:

Calculation: For a solid cylinder, its M.I. about an axis passing through centre perpendicular to its length,

Ans: Moment of inertia of given solid cylinder is .

2. A uniform solid sphere has a radius and density . Find its moment of inertia about a tangent to its surface. [July 16]

Solution:

Given:

To find: M.I of sphere about a tangent to its surface

Formula:

Calculations:

Ans: Moment of inertia of solid sphere about a tangent to its surface is .

3. A uniform solid sphere has radius and density . Find the moment of inertia about the tangent to its surface.

Solution:

Given:

To find: Moment of inertia (I)

Formulae: i.

ii. Mass volume density

Calculation: From formula (ii),

From formula (i),

A M. M. of the uniform solid sphere about a tangent – b its surface is .

4. The radius of gyration of a body about an axis, at a distance of from its centre of mass is . Find its radius of gyration about a parallel axis passing through its centre of mass.

Solution:

Radius of gyration about given axis parallel to the axis passing through centre of mass is,

Distance between two axes

From parallel axes theorem,

Ans: The radius of gyration about axis passing through the centre of mass is .

5. Find the radius of gyration of a rod of length about its transverse axis passing through its one end.

Solution:

Given:

To find: Radius of gyration (K)

Formulae: i. ii.

Calculation: From formulae (i) and (ii),

Ans: Radius of gyration about the transverse axis passing through one end of the rod is .

6. The M.I. of solid sphere about an axis passing through its centre is . Calculate its M.I. about a tangent passing through any point on its surface.

Solution:

Given that,

According to perpendicular axis theorem,

In case of sphere,

7. Calculate the moment of inertia of a uniform disc of mass and radius about an axis perpendicular to its length and passing through its centre.

Ans: M.I. of uniform disc about an axis perpendicular to its length and passing through its centre,

8. The surface density of a uniform disc of radius is . Find its MI about an axis passing through its centre and perpendicular to its plane.

Solution:

Given:

To find:

Formulae: i. ii.

Calculation: From formula (i),

From formula (ii),

Ans: M.I. of the uniform disc about an axis passing through its centre and perpendicular to its plane is .

1.8 Angular Momentum or Moment of Linear Momentum

1 A wheel of moment of inertia is rotating at a speed of . Due to friction on the axis, the wheel comes to rest in 10 minutes. Calculate the angular momentum of the wheel, two minutes before it comes to rest.

Solution:

Given:

To find:

Formulae:

Angular momentum (L)

Calculation: From formula (i),

From formula (ii),

Ans: The angular momentum of the wheel, two minutes before it comes to rest would be .

Expression for Torque in Terms of Moment of Inertia

1. A torque of acting on a body produces an angular acceleration of . Find M.I. of the body. [Mar 09]

Solution:

Given:

To find: Moment of inertia (I)

Formula:

Calculation: From formula,

Ans: Moment of inertia of the body is .

1. A torque of magnitude acting on a body produces an angular acceleration of . Calculate the moment of inertia of the body.

Solution:

Given:

To find: Moment of inertia (I)

Formula:

Calculation: From formula,

Ans: Moment of inertia of the body is .

3. A body starts rotating from rest. Due to a couple of it completes 60 revolutions in one minute. Find the moment of inertia of the body.

Solution:

Given:

To find: Moment of inertia (I)

Formulae: i. ii.

Calculation: Using formula (i),

From formula (ii),

From formula (iii),

Ans: Moment of inertia of the body is .

4. A solid sphere of diameter and mass rotates about an axis through its centre. Calculate its moment of inertia. If its angular velocity changes from to in 5 seconds, calculate the torque applied.

Solution:

Given:

(Radius)

To find: Moment of inertia (I), torque

Formulae: i. M.I of sphere,

Calculation: From formula (i),

From formula (ii),

Ans: i. The moment of inertia when the angular velocity changes from to in 5 second is .

ii. The torque applied is .

5. A wheel of moment of inertia is rotating at a speed of . Due to friction on the axis, it comes to rest in 10 minutes. Calculate the average torque of the friction.

Solution:

Given: ,

To find: Torque

Formula: i. ii.

Calculation: From formula (i)

r.p.s.

From formula (ii),

Am: Average torque of the friction is .

6. An automobile engine develops while rotating at a speed of . What tarque does it deliver?

Anc

onservation of Angular Momentum

1. A horizontal disc is freely rotating about a transverse axis passing through its centre at the rate of 100 revolutions per minute. 20 gram blob of wax falls on the disc and sticks to the disc at a distance of from its axis. Moment of inertia of the disc about its axis passing through its centre of mass is . Calculate the new frequency of rotation of the disc.