HSC PHQ 03 Kinetic Theory of Gases and Radiation

03 Kinetic Theory of Gases and Radiation

Multiple Choice Questions

1. The average distance covered by a molecule between two successive collision is ………………

(A) free path

(B) constant path

(D) free path per unit time.

Ans. (C) mean free path

2. The amount of energy radiated per second by a body does not depend upon

(A) nature of surface

(B) area of surface

(D) temperature difference of the surface and surroundings

Ans. (C) mass of the body

3. The SI unit of emissive power is
(A) watt

.
(B) watt.m

Ans. (A) watt .

4. The r.m.s. velocity of the molecules moving with velocities and is ………………
(A)
(C)
(B)
(D)

Ans. (D)

5. The light from the Sun is found to have a maximum intensity near the wavelength of . Assuming the surface of the Sun as a black body, the temperature of the Sun is ………………

(Wien’s constant )
(A)
(B)
(C)
(D)

Ans. (C)

6. The substance which allows heat radiations to pass through is ………………
(A) iron
(C) wood
(B) water vapour
(D) dry air

Ans. (D) dry air

7. The co-efficient of reflection of an opaque body is . Its co-efficient of emission is ………………

(A). 0.94
(B)
(C) 0.74
(D)

Ans. (B)

8. Two copper spheres of radii and respectively are suspended in an evacuated enclosure. Each of them are at a temperature above the surroundings. The ratio of their rate of loss of heat is
(A)
(B)
(C)
(D)

Ans. (B)

9. The pressure of an ideal gas having volume (V) is , then the energy is ………………

(A) translational kinetic

(B) rotational kinetic

(D) inversely proportional to pressure

Ans. (A) translational kinetic

10. The dimensions of emissive power are
(A)
(B)
(C)

(D)

Ans. (C)

11. For polyatomic molecules having ‘ ‘ vibrational modes, the ratio of two specific heats, is ………………
(A)
(B)
(C)
(D)

Ans. (C)

12. Two gases exert pressure in the ratio and their densities are in the ratio , then the ratio of their R.M.S. velocities is ………………
(A)
(B)
(C)
(D)

Ans. (B)

13. If the pressure of an ideal gas decreases by isothermally, then its volume will ………………

(A) decrease by

(B) increase by

(D) increase by

Ans. (D) increase by

14. Find the wavelength at which a black body radiates maximum energy, if its temperature is . (Wien’s constant )
(A)
(B)

Ans. (B)

15. If the total kinetic energy per unit volume of gas enclosed in a container is , the pressure exerted by the gas is ………………

(A)
(B)
(C)
(D)

Ans. (D)

16. The kinetic energy per molecule of a gas at temperature is ………………

(A)
(B)
(C)
(D)

Ans. (B)

17. The number of degrees of freedom for a rigid diatomic molecule is ………………
(A) 3
(B) 5
(C) 6
(D) 7

Ans. (B) 5

18. The specific heat capacity of water is
(A)
(B)
(C)
(D)

Ans. (C)

19. If the kinetic energy of hydrogen is at the pressure of 1 atmosphere, then its volume is
(A) 3 litre
(B) 2 litre
(C) 1 litre
(D). 0.5 litre

Ans. (C) 1 litre

20. The root mean square speed of the molecules of a gas is proportional to ………………

( Absolute temperature of gas)
(A)
(B)
(C)
(D)

Ans. (A)

21. The average K.E. of a gas is .………………

(A) directly proportional to absolute temperature of gas

(B) directly proportional to square of absolute temperature of gas

(D) inversely proportional to absolute temperature of gas

Ans. (A) directly proportional to absolute temperature of gas

22. If ‘ ‘ is the number of molecules per unit volume and ‘ ‘ is the diameter of the molecules, the mean free path ‘ ‘ of molecules is
(A)
(B)
(C)
(D)

Ans. (C)

Theory Question

Pressure of Ideal Gas

1. On the basis of kinetic theory of gases obtain an expression for pressure exerted by gas molecules enclosed in a container on its walls.

Derive an expression for a pressure exerted by a gas on the basis of kinetic theory of gases.

Ans:

i. Let there be moles of an ideal gas enclosed in a cubical box of volume with sides of the box parallel to the coordinate axes, as shown in figure. The walls of the box are kept at a constant temperature .
ii. The gas molecules are in continuous random motion, colliding with each other and hitting the walls of the box and bouncing back.

iii. As per one of the assumptions, we neglect intermolecular collisions and consider only elastic collisions with the walls.

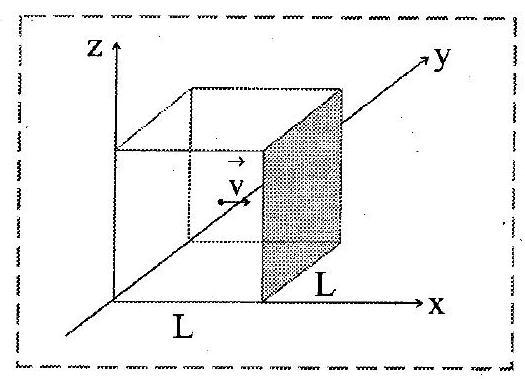
iv. A typical molecule moving with the velocity , about to collide elastically with the shaded wall of the cube parallel to yz-plane.

v. During elastic collision, the component of the velocity will get reversed, keeping and components unaltered.

vi. Hence the change in momentum of the particle is only in the component of the momentum, is given by,

final momentum – initial momentum

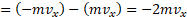
vii. Thus, the momentum transferred to the wall during collision is . The re-bounced molecule then goes to the opposite wall and collides with it.

viii. After colliding with the shaded wall, the molecule travels to the opposite wall and travels back towards the shaded wall again.

ix. This means that the molecule travels a distance of in between two collisions.

x. As is the length of the cubical box, the time for the molecule to travel back and forth to the shaded wall is .

xi. Average force exerted on the shaded wall by molecule 1 is given as,

Average force Average rate of change of momentum

where is the component of the velocity of molecule 1.

xii. Considering other molecules with the respective components of velocities , the total average force on the wall is,

…[From (2)] The average pressure

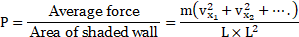
xiii. The average of the square of the component of the velocities is given by,

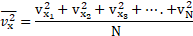
where is the average over all possible values of .

xiv. Now,

By symmetry, since the molecules have no preferred direction to move.

Therefore, average pressure

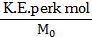
Root Mean Square (rms) Speed

1. Prove that root mean square velocity of gas molecule is directly proportional to the square root of its absolute temperature.

Show that r.m.s. velocity of a gas molecule is directly proportional to the square root of the absolute temperature of the gas.

Assuming the expression for pressure of an ideal gas, show that R.M.S. velocity of gas molecule is directly proportional to the square root of its absolute temperature.

Ans:

i. Average value of the pressure of the gas is,

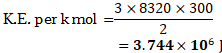
ii. Thus, the mean square velocity of molecule will be,

iii. Using ideal gas equation,

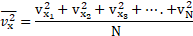
But,

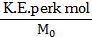
Also, (Molar mass of the gas)

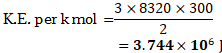
iv. Thus,

Interpretation of Temperature in Kinetic Theory

1. On the basis of the kinetic theory of gases, derive an expression for the pressure exerted by a gas.

Deduce Boyle’s law on the basis of kinetic theory of gases.

Ans:

i. Suppose, pressure exerted by the gas

volume of the gas

number of molecules of the gas

mass of each molecule of the gas.

Total mass of the gas,

ii. From kinetic theory of gases,

Pressure exerted by a gas in an enclosed vessel,

iii. But, constant for all the gases at a given temperature.

number of molecules which is constant for a given mass of the gas.

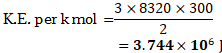
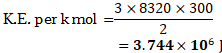
Hence, at constant temperature, pressure of the gas is increased if its volume is reduced.

2. State Boyle’s law. On the basis of kinetic theory of gases, obtain an expression for kinetic energy per unit volume of gas.

Ans: Statement: At constant temperiturie, the pressure exerted by a fixed mass of a gas is inversely proportional to the volume occupied by the gas.

Expression for kinetic energy per unit volume of gas:

i. From kinetic theory of gases pressure of the gas is given as,

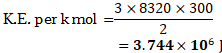
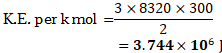
ii. The quantity represents the average translational kinetic energy of an ideal gas molecule.

iii. Therefore, the total energy of the gas is,

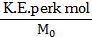
iv. Substituting in equation (1),

v. Hence, the average kinetic energy per unit volume will be,

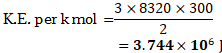
bsorption, Reflection and Transmission of Heat Radiation

1. Define : a. Coefficient of absorption

b. Coefficient of reflection

c. Coefficient of transmission.

Ans:

i. Coefficient of absorption: The ratio of amount of heat absorbed to total quantity of heat incident is called the coefficient of absorption.

ii. Coefficient of reflection: The ratio of amount of radiant energy reflected to the total energy incident is called the coefficient of reflection.

iii. Coefficient of transmission: The ratio of amount of radiant energy transmitted to total energy incident is called the coefficient of transmission.

erfect Blackbody

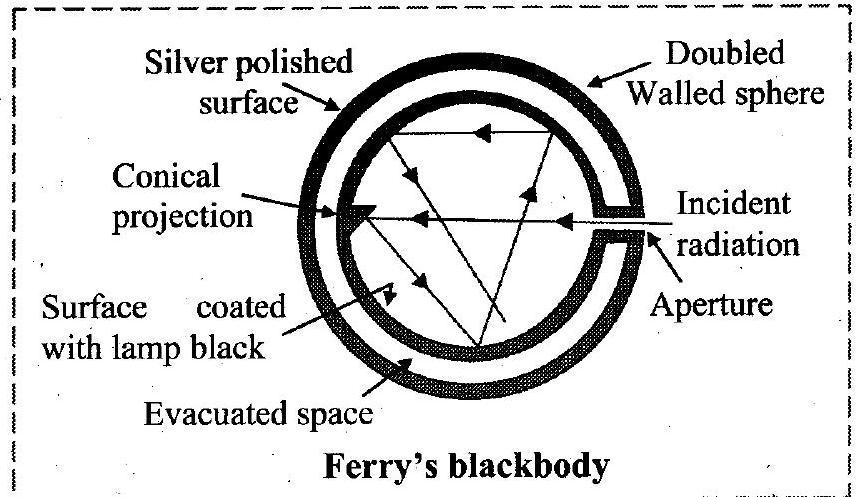
1. What is perfectly black body? Draw a neat labelled diagram of artificial perfectly black body.

Ans: Definition: body, which absorbs the entire radiant energy incident on it, is called an ideal or perfect blackbody.

2. With a neat and labelled diagram, explain Ferry’s perfectly blackbody.

Ans:

i. Ferry’s perfectly blackbody consists of a double walled hollow sphere having tiny hole or aperture, through which radiant heat can enter.

Refer subtopic 3.11: Q. No. 1 for diagram.

ii. The space between the walls is evacuated and outer surface of the sphere is silvered.

iii. The inner surface of sphere is coated with lampblack.

iv. There is a conical projection on the inner surface of sphere opposite the aperture. The projection ensures that a ray travelling along the axis of the aperture is not incident normally on the surface and is therefore not reflected back along the same path.

v. A heat ray entering the sphere through the aperture suffers multiple reflections and is almost completely absorbed inside.

vi. Thus, the aperture behaves like a perfect blackbody.

vii. The effective area of perfectly blackbody is equal to the area of the aperture.

3. Draw a neat labelled diagram for Ferry’s perfectly blackbody.

Ans: Refer Subtopic 3.11: Q. No. 1 (Diagram only)

4. What is perfectly blackbody? Explain Ferry’s blackbody.

Ans: Refer Subtopic 3.11 : Q. no. 1 (Definition only) Refer Subtopic 3.11 : Q. no. 2 for explanation.

5. What is perfectly black body?

Ans: Refer Subtopic 3.11 : Q. no. 1 (Definition only)

mission of Heat Radiation

1. Define

i. Emissive power

ii. Co-efficient of emission

Define ’emissive power’ and ‘coefficient of emission’ of a body.

Ans:

i. Emissive power: The quantity of heat radiated per unit area per unit time is defined as emissive power of the body at given temperature.

The power emitted per unit area at given temperature is defined as emissive power or radiant power of the body.

i. Emissivity: The coefficient of emission or emissivity (e) of a given surface is the ratio of the emissive power of the surface to the emissive power of a perfect black surface, at the same temperature.

irchhoff’s Law of Heat Radiation and its Theoretical Proof

1. Prove Kirchhoff’s law of radiation theoretically.

Ans: Theoretical proof:

i. Consider an ordinary body A and a perfect blackbody B of identical geometric shapes placed in an enclosure. In thermal equilibrium, both bodies will be at same temperature as that of the enclosure.

ii. Let emissive power of body ,

emissive power of blackbody

coefficient ‘of absorption of body . quantity of radiant heat incident on each body in unit time and

quantity of radiant heat absorbed by the body ,

then .

iii. As the temperatures of the body and blackbody B remain the same, both must emit the same amount as they absorb in unit time.

Quantity of radiant heat absorbed by body A

Quantity of heat emitted by body

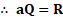
iv, For the perfect blackbody ,

v. Dividing equation (1) by equation (2), we get,

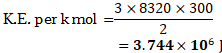
vi. But by definition of emissivity,

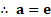
2. State and prove the Kirchhoff’s law of radiation theoretically.

Ans: Statement: At a given temperature, the ratio of emissive power to coefficient of absorption of a body is equal to the emissive power of a perfect blackbady at the same temperature for all wavelengths.

For a body emitting and absorbing thermal radiation in thermal equilibrium, the emissivity is equal to its absorptivity.

Symbolically, or

Theoretical proof: Refer Subtopic 3.13: Q. No. 1

3.14 Spectral Distribution of Blackbody Radiation

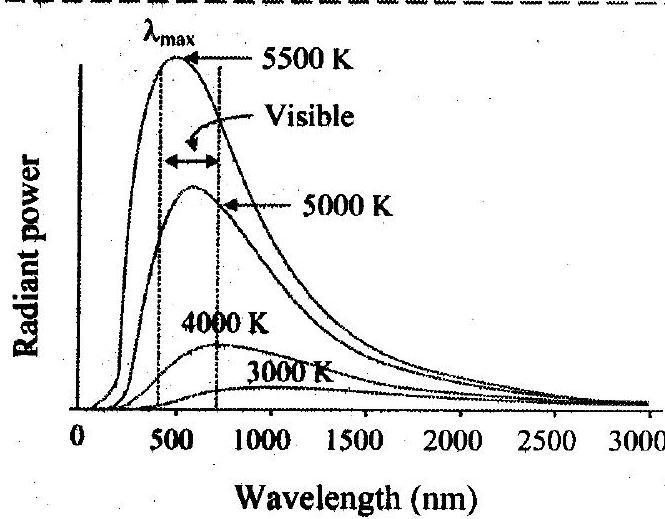
1. Represent graphically energy distribution of a black body against wavelength at various temperatures.

Ans:

Wavelength (nm)

Spectral distribution of blackbody radiation

2. Explain blackbody radiation spectrum in terms of wavelength.

Ans:

i. The rate of emission per unit area or power per unit area of a surface is defined as a function of the wavelength of the emitted radiation.

ii. Scientists studied the energy distribution of blackbody radiation as a function of wavelength.

iii. By keeping the source of radiation (such as a cavity radiator) at different temperatures they measured the radiant power corresponding to different wavelengths. The measurements were represented graphically in the form of curves showing variation of radiant power per unit area as a function of wavelength at different constant temperatures as shown in figure.

Refer Subtopic 3.14: Q. No. 1 for figure.

3. Show graphical representation of energy distribution spectrum of perfectly blackbody.

Ans: Refer Subtopic 3.14: Q. No. 1(Diagram only)

4. State Wien’s displacement law. [Mar 15]

Ans: The wavelength, for which emissive power of a blackbody is maximum is inversely proportional to the absolute temperature of the blackbody.

6. Explain energy distribution spectrum of a black body radiation in terms of wavelength.

Ans: Refer Subtopic 3.14: Q. No. 2

Numericals

Root Mean Square (rms) Speed

1. The velocities of three molecules of a gas are and respectively. Find the mean velocity and R.M.S. velocity of molecules.

Solution:

Given:

To find: Mean velocity ( ,

R.M.S velocity (

Formulae: i.

Calculation: From formula (i),

From formula (ii),

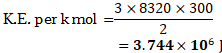
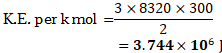
Ans: The mean velocity and r.m.s velocity of the molecules is and respectively.

2. Compute the temperature at which the r.m.s. speed of nitrogen molecules is .

[Universal gas constant, mole , molecular weight of nitrogen .]

Solution:

Given: mole ,

To find: Temperature (T)

Formula:

Calculation: From formula,

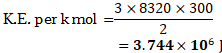
Ans: The r.m.s. speed of nitrogen molecules is at or .

Interpretation of Temperature in Kinetic Theory

1. Calculate the kinetic energy of grams of Argon molecules at .

[Universal gas constant mole , Atomic weight of Argon = 40]

Solution:

Given: mole ,

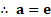
To find: Kinetic energy (K.E)

Formula:

Calculation: From formula,

K.E for 10 gram of Argon

Ans: The kinetic energy of 10 grams of Argon molecules at is .

v. A heat ray entering the sphere through the aperture suffers multiple reflections and is almost completely absorbed inside.

vi. Thus, the aperture behaves like a perfect blackbody.

vii. The effective area of perfectly blackbody is equal to the area of the aperture.

3. Draw a neat labelled diagram for Ferry’s perfectly blackbody.

Ans: Refer Subtopic 3.11: Q. No. 1 (Diagram only)

4. What is perfectly blackbody? Explain Ferry’s blackbody.

Ans: Refer Subtopic 3.11 : Q. no. 1 (Definition only) Refer Subtopic 3.11 : Q. no. 2 for explanation.

5. What is perfectly black body?

Ans: Refer Subtopic 3.11 : Q. no. 1 (Definition only)

mission of Heat Radiation

1. Define

i. Emissive power

ii. Co-efficient of emission

Define ’emissive power’ and ‘coefficient of emission’ of a body.

Ans:

i. Emissive power: The quantity of heat radiated per unit area per unit time is defined as emissive power of the body at given temperature.

The power emitted per unit area at given temperature is defined as emissive power or radiant power of the body.

ii. Emissivity: The coefficient of emission or emissivity (e) of a given surface is the ratio of the emissive power of the surface to the emissive power of a perfect black surface, at the same temperature.

irchhoff’s Law of Heat Radiation and its Theoretical Proof

1. Prove Kirchhoff’s law of radiation theoretically. [July 17]

Ans: Theoretical proof:

i. Consider an ordinary body and a perfect blackbody B of identical geometric shapes placed in an enclosure. In thermal equilibrium, both bodies will be at same temperature as that of the enclosure.

ii. Let = emissive power of body ,

emissive power of blackbody

coefficient of absorption of body . quantity of radiant heat incident on each body in unit time and

quantity of radiant heat absorbed by the body ,

then .

iii. As the temperatures of the body and blackbody B remain the same, both must emit the same amount as they absorb in unit time.

Quantity of radiant heat absorbed by body A Quantity of heat emitted by body

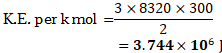
iv. For the perfect blackbody B,

v. Dividing equation (1) by equation (2), we get,

vi. But by definition of emissivity,

2. State and prove the Kirchhoff’s law of radiation theoretically.

Ans: Statement: At a given temperature, the ratio of emissive power to coefficient of absorption of a body is equal to the emissive power of a perfect blackbody at the same temperature for all wavelengths.

For a body emitting and absorbing thermal radiation in thermal equilibrium, the emissivity is equal to its absorptivity.

Symbolically, or

Theoretical proof: Refer Subtopic 3.13: Q. No. I

3.14 Spectral Distribution of Blackbody Radiation

1. Represent graphically energy distribution of a black body against wavelength at various temperatures.

Ans:

Spectral distribution of blackbody radiation

1. Explain blackbody radiation spectrum in terms of wavelength.

Ans:

i. The rate of emission per unit area or power per unit area of a surface is defined as a function of the wavelength of the emitted radiation.

ii. Scientists studied the energy distribution of blackbody radiation as a function of wavelength.

Refer Subtopic 3.14: Q. No. 1 for figure.

3. Show graphical representation of energy distribution spectrum of perfectly blackbody.

Ans: Refer Subtopic 3.14: Q. No. 1(Diagram only)

4. State Wien’s displacement law.

Ans: The wavelength, for which emissive power of a blackbody is maximum is inversely proportional to the absolute temperature of the blackbody.

5. Explain energy distribution spectrum of a black body radiation in terms of wavelength.

Ans: Refer Subtopic 3.14: Q. No. 2

Numericals

Root Mean Square (rms) Speed

1. The velocities of three molecules of a gas are and respectively. Find the mean velocity and R.M.S. velocity of molecules.

Solution:

Given:

To find: Mean velocity ( ,

R.M.S velocity (

Formulae: i.

ii.

Calculation: From formula (i),

From formula (ii),

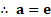
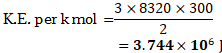
Ans: The mean velocity and r.m.s velocity of the molecules is and respectively.

2. Compute the temperature at which the r.m.s. speed of nitrogen molecules is .

[Universal gas constant, mole , molecular weight of nitrogen .] [Oct 15]

Solution:

Given: mole K,

To find: Temperature

Formula:

Calculation: From formula,

Ans: The r.m.s. speed of nitrogen molecules is at or .

Interpretation of Temperature in Kinetic Theory

1. Calculate the kinetic energy of grams of Argon molecules at .

[Universal gas constant mole , Atomic weight of Argon = 40] [Mar 13]

Solution:

Given: mole ,

To find: Kinetic energy (K.E)

Formula:

Calculation: From formula,

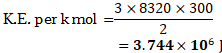
K.E for 10 gram of Argon

Ans: The kinetic energy of 10 grams of Argon molecules at is .

2. The kinetic energy of nitrogen per unit mass at is . Find the kinetic energy of oxygen at . [Molecular weight of nitrogen , Molecular weight of oxygen ]

Solution:

Given:

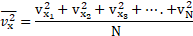
To find: Kinetic energy

Formula:

Calculation: From formula,

Ans: The kinetic energy of oxygen at is .

3. Calculate the average molecular kinetic energy:

i. per kilomole,

ii. per kilogram, of oxygen at .

mole K, Avogadro’s number mole

Solution:

Given:

To find: i. Average K.E. per kilomole

ii. Average K.E. per

Formulae: i. Average K.E. per k mol

ii. Average K.E. per

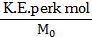
Calculation: From formula (i),

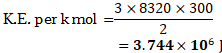
From formula (ii),

Ans: i. Average molecular kinetic energy per kilomole is .

ii. Average molecular kinetic energy per kilogram is .

4. At what temperature will average kinetic energy of gas be exactly half of its value at N.T.P.?

Solution:

Kinetic energy of gas

K.E.

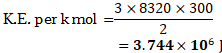
Ans: At , the average kinetic energy of the gas will be exactly half of its value at N.T.P.

3.9 Specific Heat Capacity

1. The difference between the two molar specific heats of a gas is . If the ratio of the two specific heats is 1.5 , calculate the two molar specific heats.

Solution:

Ans: The value is and is .

3.15 Stefan-Boltzmann Law of Radiation

1. A pinhole is made in a hollow sphere of radius whose inner wall is at temperature . Find the power radiated per unit area. [Stefan’s constant , emissivity

Solution:

Given: ,

To find: Power radiated

Formula:

Calculation: From formula,

Ans: The power radiated per unit area is .

2. Calculate the energy radiated in half a minute by a black body of surface area at . [July 22 ]

Solution:

Given:

To find:

Formula: Energy radiated

Calculation: From formula,

Ans: Energy radiated in one minute is .

3. Compare the rate of loss of heat from a metal sphere at with rate of loss of heat from the same at , if the temperature of surrounding is .

Solution:

Given: ,

To find: The ratio of rate of loss of heat

Formula:

Calculation: From formula,

Ans: The ratio of rate of loss of heat is 182 : 29.