HSC PYQ 14 Dual Nature of Radiation and Matter

Day

Night

14 Dual Nature of Radiation and Matter

Multiple Choice Questions

1. The de-Broglie wavelength of 1mg grain of sand blown by a wind at the speed of 20 m/s is …………….. [h=6.63×10-34 S.I. Unit ]
(A) 33.15×10-36 m
(B) 33.15×10-33 m

Ans. (B) 33.15×10-33 m

2. The photoelectric threshold wavelength of certain metal is 3315 A.U. Then its work function is……………..

(A) 6×10-19 J
(B) 7.286×10-19 J
(C) 9×10-19 J
(D) 9.945×10-19 J

Ans. (A) 6×10-19 J

3. Let ‘ p ‘ and ‘ E ‘ denote the linear momentum and energy of emitted photon respectively. If the wavelength of incident radiation is increased……………..

(A) both p and E increase.

(B) p increases and E decreases.

(D) both p and E decrease.

Ans. (D) both p and E decrease.

4. The number of photoelectrons emitted……………..

(A) varies inversely with frequency

(B) varies directly with frequency

(D) varies directly with intensity

Ans. (D) varies directly with intensity

5. When radiations of wavelength 1 and 2 are incident on certain photosensitive material, the energies of electron ejected are E1 and E2 respectively, such that E1>E2. Then Planck’s constant ‘ h ‘ is……………..

( c= velocity of light)

(A) E1-E21-2c12
(B) E1-E21c1-22
(C) E1-E212c2-1
(D) 2-1cE1-E212

Ans. (C) E1-E212c2-1

6. If the frequency of incident light falling on a photosensitive material is doubled, then the kinetic energy of the emitted photoelectron will be

(A) same as its initial value.

(B) two times its initial value.

(D) less than two times its initial value.

Ans. (C) more than two times its initial value.

7. The momentum of a photon of de Broglie wavelength 5000Å is……………..

[Planck’s constant =6.63×10-34 J.s.]

(A) 1.326×10-28 kg-m/s

(B) 7.54×10-28 kg-m/s

(D) 7.54×10-27 kg-m/s

Ans. (C) 1.326×10-27 kg-m/s

8. The energy of photon of wavelength is …………….. [h= Planck’s constant, c= speed of light in vacuum]

(A) hch
(B) hc
(C) hc
(D) hc

Ans. (D) hc

9. The kinetic energy of emitted photoelectrons is independent of……………..

(A) frequency of incident radiation.

(B) intensity of incident radiation.

(D) collector plate potential.

Ans. (B) intensity of incident radiation.

10. In a photon-electron collision ……………..

(A) only total energy is conserved.

(B) only total momentum is conserved.

(D) both total momentum and total energy are not conserved.

Ans. (C) both total energy and total momentum are conserved.

11. The momentum associated with photon is given by……………..

(A) h
(B) hvc
(C) hE
(D) h

Ans. (B) hvc

12. In a photocell, increasing the intensity of incident light increases……………..

(A) the stopping potential

(B) the photoelectric current

(D) maximum kinetic energy of the photoelectron

Ans. (B) the photoelectric current

13. An electron of energy 150eV has wavelength of 10-10 m. The wavelength of a 0.60keV electron is
(A) 0.50Å
(B) 0.75Å
(C) 1.2Å
(D) 1.5Å

Ans. (A) 0.50Å

14. If the maximum kinetic energy of emitted electrons in photoelectric effect is 2eV, the stopping potential will be……………..
(A) 0.5 V
(B) 1.0 V
(C) 1.5 V
(D) 2.0 V

Ans. (D) 2.0 V

Theory Questions

14.2 The Photoelectric Effect

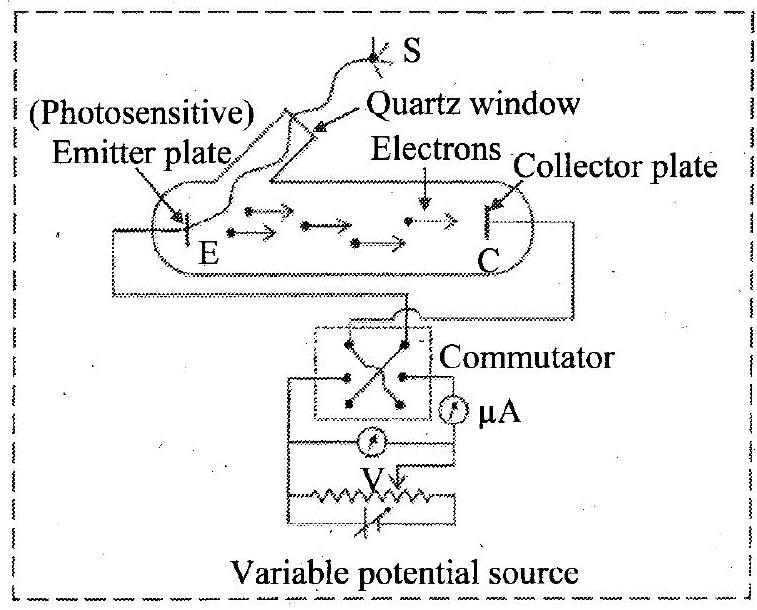
Draw a neat labelled circuit diagram of experimental arrangement for study of photoelectric effect.

Ans: Circuit diagram of experimental set-up for study of photoelectric effect:

State Einstein’s photoelectric equation.

Ans: Einstein’s photoelectric equation:

K.E. max =hv-0.

What is photoelectric effect?

Define:

i. Stopping potential

ii. Photoelectric work function.

Ans: The phenomenon of emission of electrons from a metal surface, when radiation of appropriate frequency is incident on it, is known as photoelectric effect.

i. If increasingly negative potentials were applied to the collector in experiment of photoelectric effect, the photocurrent decreases and for some typical value -V0, photocurrent becomes zero. This value of V0 is termed as cut-off or stopping potential.

ii. The minimum amount of energy required to be provided to an electron to pull it out of the metal from the surface is called the work function of the metal.

Define:

i. Threshold frequency

ii. Photoelectric work function

Ans:

i. The minimum frequency of incident radiation required to start a photoemission in any photosensitive material is known as threshold frequency.

ii. Refer Subtopic 14.2: Q. No. 3.(ii).

Is it always necessary to use red light to get photoelectric effect?

[Mar 22]

Ans: No. Any light possessing sufficient energy to initiate the photoemission can be used to get photoelectric effect.

How does the wave theory of light fail to explain the observations from experiment on photoelectric effect? [Give any two points]

Ans: The wave theory of electromagnetic radiation could not explain following observations of photoelectric effect.

i. According to wave theory, the metal surface will require reasonable time to accumulate sufficient energy to knock off electrons. However, the ejection of electrons is an instantaneous process.

ii. Since larger incident intensity implies larger energy, the electrons are expected to be emitted with larger kinetic energy. But the observation showed that the maximum kinetic energy did not depend on the incident intensity but depended on the incident frequency.

iii. Wave theory expected photoelectrons to be emitted for any frequency. But observations indicated that for a given metal surface, some characteristic cut-off frequency v0 existed below which no photoelectrons were emitted however intense the incident radiation was.

(Any two points)

With neat labelled circuit diagram, describe an experiment to study the characteristics of photoelectric effect.

Describe an experiment for the study of characteristics of photoelectric effect.

Ans: Refer Subtopic14.2: Q. No. 1 for Circuit diagram of experimental set-up

i. A laboratory experimental set-up for the photoelectric effect consists of an evacuated glass tube with a quartz window.

ii. The glass tube contains photosensitive metal plates. One is the emitter E and another plate is the collector C.

iii. The emitter and collector are connected to a voltage source whose voltage can be changed and to an ammeter to measure the current in the circuit.

iv. A potential difference of V, as measured by the voltmeter, is maintained between the emitter E and collector C. Generally, C (the anode) is at a positive potential with respect to the emitter E (the cathode).This potential difference can be varied and C can even be at negative potential with respect to E. v : When the anode potential (V) is positive, it accelerates the electrons. This potential is called accelerating potential. When the anode potential (V) is negative, it retards the flow of electrons. This potential is known as retarding potential.

vi. A source S of monochromatic light of sufficiently high frequency (short wavelength 10-7 m ) is used.

14.4 Photo Cell

Draw a well labelled diagram of photoelectric cell.

Ans:

Describe the construction of photoelectric cell.

Ans: Construction of photoelectric cell:

i. A photo cell consists of a semi-cylindrical photosensitive metal plate E acting as a cathode and a wire loop collector C acting as an anode supported in an evacuated glass or quartz bulb.

ii. The electrodes are connected to an external circuit having a high tension battery B and a micro ammeter A.

iii. Instead of a photosensitive metal plate, the photosensitive material can be pasted in the form of a thin film on the inner walls of the glass bulb.

14.5 De Broglie Hypothesis

Derive an expression for de Broglie wavelength of an electron moving under a potential difference of V volt.

Ans:

i. Consider an electron of mass m and charge q is accelerated through potential difference of V volts.

ii. According to de Broglie hypothesis, wavelength of any particle is,

=hp=hmv

∵ p=mv

∴ m2v2=p2

∴ 12mv2m=12p2∴ E=p22 m

∴p=2mE

∴ =h2mE

iii. Now, for an electron accelerated through potential difference V, the work done on the electron is stored in it in the form of energy.

∴ E=qV

∴ =h2mE=h2mqV

iv. But, q=1.6×10-19C,m=9.1×10-31 kg, h=6.63×10-34 J-s

∴ =h2mqV

=6.63×10-342×9.1×10-31×1.6×10-19×V( in volts )

=1.228×10-9V( in volts )m

i.e., =1.228V( in volts )nm

What is de-Broglie hypothesis? Obtain the relation for de-Broglie wavelength.

Explain de Broglie wavelength. Obtain an expression for de Broglie wavelength of wave associated with material particles.

State de-Broglie’s hypothesis of matter waves and derive an expression for de-Broglie wavelength.

Ans:

i. De Broglie proposed that a moving material particle of total energy E and momentum p has a wave associated with it (analogous to a photon).

ii. He suggested a relation between properties of wave, like frequency and wavelength, with that of a particle, like energy and momentum.

p=Ec=hc=h

iii. Thus frequency and wavelength of a wave associated with a material particle, of mass m moving with a velocity v, are given as

v=Eh and =hp=hmv

iv. De Broglie referred to these waves associated with material particles as matter waves. The wavelength of the matter waves, given by equation (1), is now known as de Broglie wavelength and the equation is known as de Broglie relation.

14.6 Davisson and Germer Experiment

Draw a neat labelled diagram of Davisson and Germer experiment.

Ans:

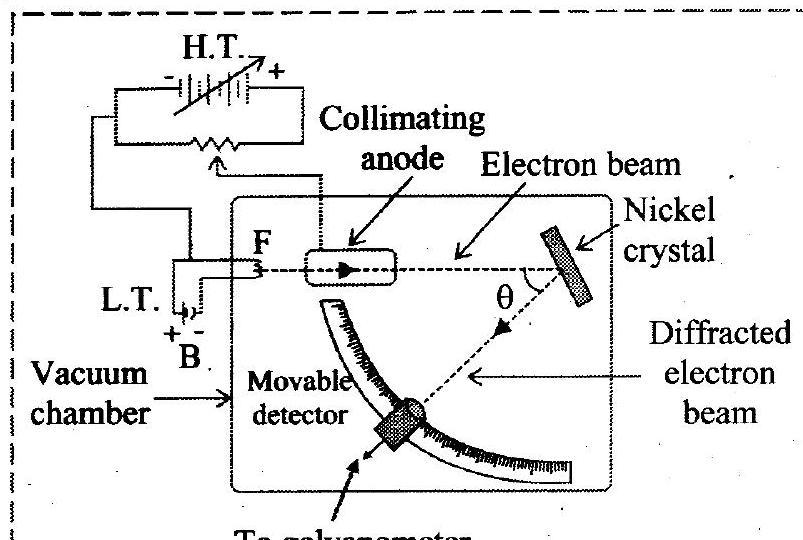
To galvanometer

Schematic of Davisson and Germer experiment

Numericals

14.2 The Photoelectric Effect

The threshold wavelength for silver is 3800Å. Calculate maximum kinetic energy in eV of photoelectrons emitted when ultraviolet light of wavelength 2600Å falls on it. Also calculate stopping potential.

[1eV=1.6×10-19 J, Plank’s constant =6.63×10-34 J-s, speed of light in vacuum =3×108 m/s]

Solution:

Given: 0=3800Å=3.8×10-7 m,=2600Å=2.6×10-7 m

To find. Maximum kinetic energy (K.E.max),

Stopping potential V0

Formulae: i. K. Emax=hc1-10

ii. K.E Emax=eV0

Calculation: From formula (i),

K.Emax =6.63×10-34×3×10810-712.6-13.8 =6.63×3×10-19(3.8-2.6)2.6×3.8=2.42×10-19 J=2.42×10-191.6×10-19=1.51eV

From formula (ii),

eV0=1.51eV

V0=1.51V

Ans: Maximum kinetic energy is 1.51eV, stopping potential is 1.51 V.

The photoelectric work function for a metal is 4.2eV. If the stopping potential is 3 V, find the threshold wavelength and maximum kinetic energy of emitted electrons.

[Velocity of light in air =3×108 m/s, Planck’s constant =6.63×10-34 J-s, Charge on electron =1.6×10-19C]

Solution:

Given:

0=4.2eV=4.2×1.6×10-19=6.72×10-19 J,

V0=3 V, h=6.63×10-34 J-s,e=1.6×10-19C,c=3×108 m/s,

To find: i. Threshold wavelength 0,

ii. Maximum kinetic energy (K.E Emax)

Formulae: i. 0=hc0

ii. V0=K⋅Emaxe

Calculation: i. From formula (i),

0 = hc W0=6.63×10-34×3×1086.72×10-19=6.63×36.7210-7 ={antilog⁡[log⁡(6.63)+log⁡(3)-log⁡(6.72)]}×10-7 ={antilog⁡[0.8215+0.4771-0.8274]}×10-7 ={ antilog [0.4712]}×10-7 =2.959×10-7 m

∴ 0=2959Å

ii. From formula (ii),

K.Emax=V0×e =3×1.6×10-19 =4.8×10-19 J

Ans: i. Threshold wavelength is 2959Å.

ii. Maximum kinetic energy of the emitted electrons is 4.8×10-19 J.

Find the wave number of a photon having energy of 2.072eV.

Given: Charge on electron =1.6×10-19C

Velocity of light in air =3×108 m/s

Planck’s constant =6.63×10-34 J-s.

Solution:

E=2.072eV=2.072×1.6×10-19 J,e=1.6×10-19C,

c=3×108 m/s,h=6.63×10-34 J-s

To find: Wave number (v‾)

Formula: v‾=1=Ech

Calculation: From formula,

v‾ =2.072×1.6×10-193×108×6.63×10-34 ∴ v‾ =2.072×1.63×6.63107 ={antilog⁡[log⁡(2.072)+log⁡(1.6)-log⁡(3.0)-log⁡(6.63)]}×107 ={antilog⁡[0.3164+0.2041-0.4771-0.8215]}×107 ={antilog⁡(1.2219)}×107 =0.1666×107 v‾ =1.6661106 m-1

Ans: The wave number is 1.666×106 m-1.

The photoelectric threshold wavelength of a metal is 230 nm. Determine the maximum kinetic energy in joule and in eV of the ejected electron for the metal surface when it is exposed to a radiation of wavelength 180 nm.

[Planck’s constant : h=6.63×10-34Js, Vélocity of light : c=3×108 m/s.]

Solution:

Given:

0=230 nm=230×10-9 m,=180 nm=180×10-9 m, h=6.63×10-34 J s,c=3×108 m/s,

To find: K.E. (in joule and eV )

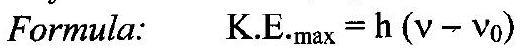
Calculation: Using formula,

K.E. max=hc-c0=hc1-10=hc0-0 =6.63×10-34×3×1081180×10-9-1230×10-9 =6.63×3×10-2610-823-1823×18=6.63×3×523×1810-18 ={antilog⁡[log⁡(6.63)+log⁡(3)+log⁡(5)-log⁡(23)-log⁡(18)]}×10-18 ={ antilog [0.8215+0.4771+0.6990-1.3617-1.2553]}×10-18 ={antilog⁡[1.9976-2.6170]}×10-18 ={antilog⁡[1.3806]}×10-18=0.2402×10-18 ∴ K.E. max=2.402×10-19 J

={antilog⁡[log⁡(2.402)-log⁡(1.6)]} ={ antilog [0.3806-0.2041]} ={ antilog [0.1765]} =1.5eV

Ans: The maximum kinetic energy of the ejected electron is 2.402×10-19 J or 1.5eV.

The threshold wavelength of silver is 3800Å. Calculate the maximum kinetic energy in eV of photoelectrons emitted, when ultraviolet light of wavelength 2600Å falls on it. (Planck’s constant, h=6.63×10-34 J.s. ., Velocity of light in air, c=3×108 m/s )

Solution:

Given: 0=3800Å=3.8×10-7 m,=2600Å=2.6×10-7 m

To find: Maximum kinetic energy (K.E.max),

Formula: K.E Emax=hc1-10

Calculation: From formula,

( K.E. )max =6.63×10-34×3×10812600×10-10-13800×10-10 =6.63×10-34×3×108(3800-2600)×10-102600×3800×10-20 =6.63×10-34×3×108×12002600×3800×10-10=6.63×3626×3810-18 ={ antilog [log⁡(6.63)+log⁡(36)-log⁡(26)-log⁡(38)]}×10-18 ={ antilog [0.8215+1.5563-1.4150-1.5798]}×10-18 ={ antilog [-0.6170]}×10-18 ={ antilog [1.3830]}×10-18 =2.416×10-110-18=2.416×10-19 J ∴ (K.E. )max (in eV) =2.416×10-191.6×10-19=1.509eV

A. Maximum kinetic energy of the photoelectron emitted is 1.509eV.

The photoelectric current in a photoelectric cell can be reduced to zero by a stopping potential of 1.8 volt. Monochromatic light of wavelength 2200Å is incident on the cathode. Find the maximum kinetic energy of the photoelectrons in joules.

Solution:

[Charge on electron =1.6×10-19C]

Given:

Formula: (K.E. )max=eV0

Calculation: Using formula,

(K.E. )max=1.6×10-19×1.8 ∴ ( K.E )max=2.8810-19J

Ans: Maximum kinetic energy of emitted photoelectron is 2.8810-19 J.

The photoelectric work function for a metal surface is 2.3eV. If the light of wavelength 6800Å is incident on the surface of metal, find threshold frequency and incident frequency. Will there be an emission of photoelectrons or not?

[Velocity of light c=3×108 m/s, Planck’s constant, h=6.63×10-34Js ]

Solution:

Given: 0=2.3eV,=6800Å=6.8×10-7 m,c=3×108 m/s,h=6.63×10-34Js

To find: i. Threshold frequency v0 ii. Incident frequency (v) iii. If emission of photoelectrons possible

Formulae: i. 0=hv0 ii. v=c

Calculation: From formula (i),

v0 =0 h=2.3×1.6×10-196.63×10-34=3.68×10156.63=36.86.631014 ={antilog⁡[log⁡(36.8)-log⁡(6.63)]}×1014 ={antilog⁡(1.5658-0.8215)}×1014 ={antilog⁡(0.7443)}×1014 =5.5501014Hz

From formula (ii)

v=3×1086.8×10-7=30×1076.8×10-7

={antilog⁡[log⁡(30)-log⁡(6.8)]}×1014

={antilog⁡(1.4771-0.8325)}×1014

={antilog⁡(0.6446)}×1014

=4.412×1014 Hz

Since incident frequency is less than threshold frequency i.e., v<v0, photoelectric emission will not be observed.

Ans: i. Threshold frequency v0 is 5.55×1014Hz. ii. Frequency of incident light is 4.412×1014Hz

iii. Emission of photoelectrons is not possible.

Light of wavelength 3000Å falls on a metal surface having work function 2.3eV. Calculate the maximum velocity of ejected electrons.

(Planck’s constant h=6.63×10-34Js, velocity of light c=3×108 m/s, mass of an electron =9.1×10-31 kg )

Solution:

Given: =3000Å=3×10-7 m, me=9.1×10-31 kg,0=2.3eV,h=6.63×10-34Js,c=3×108 m/s

To find: Maximum velocity vmax

Formulae: i. (K.E) )max=hc-0

ii. vmax=2( K.E. )maxme

Calculation: From formula (i),

( K.E. )max=6.63×10-34×3×1083×10-7-2.3×1.6×10-19=6.63×10-19-3.68×10-19=2.95×10-19

Also, 12 mevmax2=( K.E. )max

From formula (ii),

vmax =2×2.95×10-199.1×10-31=5.90×10129.1=5909.1105 =antilog⁡12[log⁡(590)-log⁡(9.1)]105 =antilog⁡12(2.7709-0.9590)105 =antilog⁡12(1.8119)105 ={antilog⁡(0.9059)}×105 =8.052105 m/s

Ans: The maximum velocity of electron is 8.052×105 m/s

The work functions for potassium and caesium are 2.25eV and 2.14eV respectively. Is the photoelectric effect possible for either of them if the incident wavelength is 5180Å ?

Solution:

[Given: Planck’s constant =6.63×10-34 J.s.; Velocity of light =3×108 m/s;1eV=1.6×10-19 J] [Mar 17]

Given:

0P=2.25eV=2.25×1.6×10-19 J=3.6×10-19 J,

0C=2.14eV=2.14×1.6×10-19 J=3.424×10-19 J,=5180Å=5.18×10-7 m

To find: Will the photoelectric effect occur for potassium and caesium with =5180Å

Formula: 0=hc0

Calculation: From formula,

0P=hc0P ∴ 0P=hc0P=6.63×10-34×3×1083.6×10-19=6.631.210-7=5.525×10-7 m=5525Å

Similarly,

0C=hc0c=6.63×10-34×3×1083.424×10-19=5.809×10-7 m=5809Å

As incident wavelength () is smaller than threshold wavelength for potassium 0P and for caesium 0C i.e, <0P<0C. Photoelectric effect is possible for both of them.

Ans: For =5180Å wavelength, both potassium and caesium will exhibit photoelectric emission.

If the work function of a metal is 3eV, calculate the threshold wavelength of that metal. [Velocity of light =3×108 m/s, Planck’s constant =6.63×10-34 J.s.,1eV=1.6×10-19 J ]

Solution:

Given: 0=3eV=3×1.6×10-19 J, h=6.63×10-34 J-s,e=1.6×10-19C,c=3×108 m/s.

To find: Threshold wavelength 0,

Formula: 0=hc0

Calculation: From formula,

0=6.63×10-34×3×1083×1.6×10-19=4.14×10-7 m

Ans: Threshold wavelength of the metal is 4.14×10-7 m.

If the total energy of radiation of frequency 1014 Hz is 6.63 J, calculate the number of photons in the radiation. [Planck’s constant =6.63×10-34 J.s.]

Solution:

Given:

E=6.63 J,v=1014 Hz, h=6.63×10-34Js

To find: Number of photons ( n )

Formula: n=Eh

Calculation: Using formula,

n=6.636.63×10-341014=1020

Ans: The number of photons emitted in the radiation are 1020.

The work function for a metal surface is 2.2eV. If light of wavelength 5000Å is incident on the surface of the metal, find the threshold frequency and incident frequency. Will there be an emission of photoelectrons or not? c=3×108 m/s,1eV=1.6×10-19 J, h=6.63×10-34Js

Solution:

Given: 0=2.2eV=2.2×1.6×10-19 J,=5000Å=5000×10-10 m, h=6.63×10-34 J.s,c=3×108 m/s

To find:

Formulae:

i. Threshold frequency v0

ii. Incident frequency (v)

iii. If photoemission is possible?

Calculation: Using formula (i),

ii. c=vλ

2.2×1.6×10-19=6.63×10-34v0

v0=2.2×1.6×10-196.63×10-34

={antilog⁡[log⁡(2.2)+log⁡(1.6)-log⁡(6.63)]}×1015

={antilog⁡[0.3424+0.2041-0.8215]}×1015

={antilog⁡(1.6250)}×1015.

=0.5309×1015

v0=5.31×1014 Hz

Using formula (ii),

3×108=v×5000×10-10

v=3×1085000×10-10

v=6×1014 Hz

As, v>v0, there will be emission of photoelectrons.

As, v>v0, there will be emission of photoelectrons.
Ans: i. Threshold frequency is 5.31×1014Hz ii. Incident frequency is 61014Hz
iii. There will be emission of photoelectrons.

The photoelectric work function for a metal surface is 3.84×10-19 J. If the light of wavelength 5000Å is incident on the surface of the metal, will there be photoelectric emission?

Solution:

Given: 0=3.84×10-19 J,=5000Å=5000×10-10 m

Energy of incident radiation (E)=hc=6.63×10-34×3×1085000×10-10=3.978×10-19 J

Here, E>0

Since E is greater than 0, photoelectric emission will occur.

Ans: Yes, photoelectric emission will occur.

The photoelectric work function for a metal is 4.2eV. Find the threshold wavelength.

Solution:

Given:

0=4.2eV=4.2×1.6×10-19 J

To find:

Threshold wavelength 0

Formula:

0=hc0

Calculation: From formula,

0=hc0

=6.63×10-34×3×1084.2×1.6×10-19 =2.9598×10-7 m =2959.8Å

Ans: The threshold wavelength is 2959.8Å.

14.5 De Broglie Hypothesis

Calculate the de-Broglie wavelength of proton if it is moving with a speed of 2×105 m/s.

Solution:

Given: v=2×105 m/s

To find: de-Broglie wavelength ()

Formula: =hmv

Calculation: We know that, h=6.63×10-34Js,

mp=1.673×10-27 kg

From formula,

=6.63×10-341.673×10-27×2×105 =6.63×10-343.346×10-22 =1.98×10-12 m

Ans: The de-Broglie wavelength of the proton is 1.98×10-12 m.

Calculate the de Broglie wavelength of an electron moving with 1/3rd of the speed of light in vacuum. (Neglect relativistic effect)

(Planck’s constant : h=6.63×10-34Js, Mass of electron : m=9.11×10-28 g )

Solution:

v=c3=3×1083=108 m/s,h=6.63×10-34Js,m=9.11×10-28 g=9.11×10-31 kg

To find: de Broglie wavelength ()

Formula: =hmv

Calculation: From formula,

=6.63×10-349.11×10-31108=66.39.1110-35103110-8=66.39.1110-12 ∴ ={antilog⁡[log⁡(66.3)-log⁡(9.11)]}×10-12 ={antilog⁡[1.8215-0.9595]}×10-12 ={antilog⁡[0.8620]}×10-12 ∴ =7.27810-12 m.

Ans: The de Broglie wavelength of electron is 7.278×10-12 m.

What is de Broglie wavelength of an electron accelerated through 25000 volt?

Solution:

Given: V=25000 volt

To find: de-Broglie wavelength ()

Formula: =12.28VÅ

Calculation: Using formula,

=12.282500010-10=12.28×10-102.5×104=12.28(2.5)1210-12

=antilog⁡log⁡(12.28)-12log⁡(2.5)10-12 =antilog⁡1.0892-12(0.3979)10-12 ={antilog⁡(0.8902)}×10-12 =7.766×10-12 m =0.07766×10-10 m=0.07766Å

Ans: The de-Broglie wavelength of electron is 0.07766Å

Calculate the de-Broglie wavelength of an electron moving with one fifth of the speed of light. Neglect relativistic effects.

(h=6.63×10-34 J.s.,c=3×108 m/s, mass of electron =9×10-31 kg)

Solution:

Given:

v=15×c=15×3×108=6×107 m/s,h=6.63×10-34 J.s,m=9×10-31 kg

To find: de-Broglie wavelength ()

Formula: =hmv

Calculation: Using formula,

=6.63×10-349×10-31×6×107 ={antilog⁡[log⁡(6.63)-log⁡(9)-log⁡(6)]}×10-10 ={antilog⁡[0.8215-0.9542-0.7782]}×10-10 ={antilog⁡[1.0891]}×10-10 =0.1228×10-10 m=0.1228Å

Ans: The de-Broglie wavelength of an electron is 0.1228Å.

An electron is accelerated through a potential difference of 100 volt. Calculate de-Broglie wavelength in nm.

Solution:

De-Broglie wavelength of an electron is given by, =1.228Vnm

∴ =1.228100=0.1228nm