1
SAMPLE PAPER
MATHEMATICS PART-II
[Time : 2 hrs] [Total Marks : 40]
1. (A) Four alternative answers are given for every sub-questions. Select the correct alternative and write the alphabet of that answers :
(i) In right-angled triangle , Hypotenuse and side , then what is the measure of ?
(A)
(B)
(C)
(D)
Solution
(B)
(ii) If , then ?
(A)
(B) 0
(C) 1
(D)
Solution
(B) 0
(iii) In the given figure, line , then find

(A)
(B)
(C)
(D)
Solution
(B)
(iv) The centroid of the triangle whose vertices are is:
(A)
(B) 6,7
(C)
(D)
Solution
(A)
(B) Solve the following questions.
(i) Which of the following conditions is not sufficient to determine the congruence of two triangles?
Solution
SSA is not sufficient condition.
(ii) “The diagonals bisect each other at right angles.” In which of the following quadrilaterals is the given property observed ?
Solution
Rhombus
Rectangle, Rhombus, Parallelogram, Trapezium.
(iii) A line is parallel to -axis and is at a distance of 5 units from the -axis. Write the equation of that line.
Solution
The equation of line is .
(iv) In and .
Then write the ratios of and from the figure.
Solution
and
2. (A) Complete and write the following activities. (Any two)

(i) From the information in the figure, complete the following activity to find the length of the hypotenuse AC.

Solution
Side opposite angle Hypotenuse
(ii) Prove that, The areas of two triangles with same height are in the proportion of their corresponding bases. To prove this theorem start as follows :
(i) Draw two triangles, give names of all points, show heights.
Solution
The triangles are :
(ii) Write ‘Given’ and ‘To prove’ from the figure drawn.
Solution
Given :
To prove :

(iii) Theorem: Opposite angles of a cyclic quadrilateral are supplementary.
Given: is cyclic
To prove:
Proof: Arc ABC is intercepted by the inscribed angle
Similarly, is an inscribed angle. It intercepts arc ADC.
Similarly,
Solution
Given: is cyclic
To prove:
Proof: arc
Similarly, is an inscribed angle.
Similarly, we can proof
(B) Solve the following sub-questions.
(i) If length of the circular arc is and the radius , find the area of the sector of the circle.
Solution
Length of the circular .
Radius .
Length of the circular arc
Hence, the area of the sector is . .
(ii) Base of a triangle is 9 and height is 5 . Base of the another triangle is 10 and height is 6 . Find the ratio of areas of these triangles.
Solution
Here, Area of first triangle
(iii) In the figure, the centre of the circle is and .

(i) ? By which theorem ?
Solution
Hence, (arc SP) is by inscribed angle theorem.
(ii) ? Give reason.
Solution
Hence, SOP is because the measure of an angle subtended by an arc at the centre of the circle is double the measure of the angle subtended by the arc at any point on the circle.
(iv) Draw a circle of suitable radius. Take point on it. Draw a tangent through point .
Solution
Steps of construction :
(i) Draw a circle with centre .
(ii) Take any point on the circle and join OT and extend it to .
(iii) Take points and on and respectively i.e. .
(iv) Taking A as centre and radius greater than AT, draw two arcs on both side of OX.
(v) Taking B as centre and radius greater than BT, draw

two arcs intersecting the arcs drawn in step (iv).
(vi) Join the arcs to obtain the line LM, passing through point T. Line is the required tangent to the circle at point .
(v) If and point divides seg in the ratio , then find coordinates of point .
Solution
Here, and
According to section formula,
Coordinates of are .
3. (A) Complete and write the following activities: (Any one)(Marks 3)
(i) Prove that .
Proof: L.H.S.
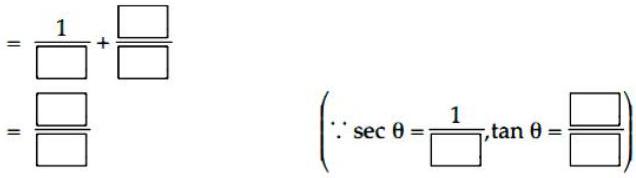
[Multiplying with the numerator and denominator]

R.H.S.
L.H.S. R.H.S.
Solution
Proof: L.H.S.
[Multiplying with the numerator and denominator]
L.H.S. R.H.S.
(ii) Find distance between points and .
By distance formula,
Solution
By distance formula,
(B) Solve the following sub-questions.
(i) If , then find the values of .
Solution
From the table of T-ratios,
We know that
(ii) If point divides the line segment with and in the ratio , find the coordinates of .
Solution
By section formula
(iii) Draw . In and .
Solution
Steps of construction :
(i) Draw segment .
(ii) Draw ray such that .
(iii) Take point on ray such that .
(iv) Join TQ.
is obtained.
(v) Divide segment into 3 equal parts.
(vi) Fix point on such that length of is of length of segment PQ.

(vii) Draw a line parallel to side TQ, through .
(viii) Name the point of intersection of the line and ray PT as .
Thus, we get required similar to .
(iv) In the figure with are the mid-points of and respectively. Then prove that the four triangles formed are congruent to each other.

Solution
(iv) Given : is a triangle and and are respectively the mid-points of sides , and .
To prove : is divided into 4 congruent triangles.
Proof : and are the mid-points of and of .
So, PQ II BC … [Line segment joining the mid-points of two sides of a triangle is parallel to the third side]
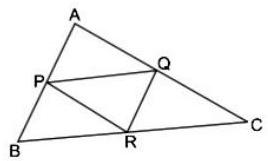
Similarly, and
In PQRB, and …[Parts of parallel lines are parallel] i.e., both pairs of opposite sides are parallel.
Thus, PQRB is a parallelogram.
So, is a diagonal of parallelogram .
So,
…[A diagonal of a parallelogram divides it into two congruent triangles.]
Similarly, APRQ is a parallelogram
So,
and is a parallelogram
So,
From equations (i), (ii) and (iii),
Hence, all 4 triangles are congruent to each other.
4. Solve the following sub-questions.
(i) In fig., the circles with centres and touch each other at R. A line passing through R meets the circles at and respectively. Prove that:
(a) seg AP II seg BQ
Solution
The circles with centres and touch each other at .
By theorem of touching circles .
(a) In PAR
Seg
Hence Proved.
(Radii of same circle)
Similarly, in
[Isosceles triangle theorem)
(Radii of the same circle)
…(ii) [Isosceles triangles theorem]
But …(iii) [Vertically opposite angles]
…(iv) [From (i) & (ii)]
But, they are a pair of alternate angles formed by transversal on seg and seg BQ.
seg AP II seg BQ [Alternate angles test]
(b) and
Solution
In and
[From (i) & (iii)]
(c) find , if
Solution
In
(ii) In , then find and .
Solution
In ,
By theorem,

(iii) Walls of two buildings on either side of a street are parallel to each other. A ladder long is placed on the street such that its top just reaches the window of a building at the height of . On turning the ladder over to the other side of the steet, its top touches the window of the other building at a height . Find the width of the street.

Solution

In the figure, seg and represent the walls of two buildings on either side of a street . segment represents the first portion of the ladder and seg. CE represents the second position of the ladder.
In
In
By Pythagoras theorem.
Width of the street is .
5. Solve the following sub-questions.
(i) If and are real numbers and , if and are the sides of the triangle, then prove that the triangle is right angled. (Use the converse of the Phythogoras theorem). Find out two Pythagorian triplets using convenient values of and .
Solution
Given : , sides of the triangle are and .
To prove : The triangle is right-angled triangle
Proof :
Since, both sides are equal,
So, by the converse of Pythagoras theorem, given triangle is right-angled triangle.
Pythagorean triplets | ||||
and | ||||
and |
Hence, two Pythagorean triplets are and .
(ii) Diagonals of a quadrilateral intersect in point . If , then prove that .

Solution
Given :
To prove :
Proof:
In and